Дополнение B. Дерево индексации в твердотельных устройствах

В этом разделе мы представим архитектуру FD- дерева. Наша цель состоит в минимизации общего числа небольших произвольных записей и ограничить эти произвольные записи в пределах небольшой области и в то же время предоставлять высоко эффективный поиск. Для простоты мы предполагаем уникальность всех ключей индексации в неком FD- дереве. Применяемая на протяжении этой статьи нотация сведена в Таблице B-1

Таблица B-1. Применяемые в этой статье параметры

Параметры	Описание
B	размер страницы (байты)
Li	iй уровень FD- дерева
|Li|	ёмкость Li (общее число вхождений)
l	число уровней FD- дерева
k	логарифмическое соотношение размеров между соседними уровнями
n	число записей в данном соотношении индексации
f	число вхождений в странице

В своём проекте для некой индексации во флэш SSD мы рассмотрим три таких принципа.

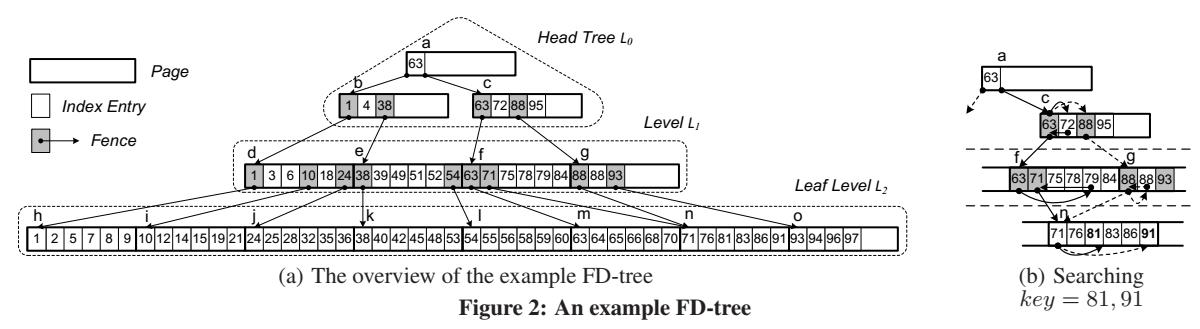
Некое FD- дерево составляется из множества уровней, обозначаемых как L₀ ~ L_i-1. Самый верхний уровень, L₀, является небольшим B⁺- деревом, именуемым головным деревом. Размер соответствующего узла этого головного дерева равняется размеру страницы B его флеш SSD. Всякий последующий уровень, L_i (1 ≤ i < l) являются отсортированными прогонами (run) в непрерывных страницах. Рисунок B-2 a) иллюстрирует структуру некого FD- дерева. Это FD- дерево имеет три уровня, само головное дерево и два сортированных прогона. Его головное дерево является двухуровневым B⁺- деревом. С помощью технологии фрагментарного каскадирования (fractional cascading), определённые листовые узлы данного головного дерева содержат указатели на сортированный прогон L₁. Все нелистовые уровни в FD- дереве содержат указатели на сортированные прогоны на уровень непосредственно ниже своего.

Каждый уровень FD- дерева обладает некой ёмкостью (capasity) в терминах вхождений, обозначаемой как |L_i|. Следуя логарифмическому методу, мы устанавливаем уровни с некой пошаговой ёмкостью, т.е. |L_i+1| = k ∙ |L_i| (0 ≤ i ≤ l-2), где k это значение логарифмического соотношения размеров между соседними уровнями. Таким образом, |L_i| = kⁱ ∙ |L₀|. Все обновления первоначально выполняются в установленном головном дереве, а затем постепенно мигрируют в сортированные прогоны на нижние уровни пакетно по мере расходования установленной ёмкости уровня. Следуя принципу проектирования П2, величина максимального размера установленного головного дерева устанавливается равным размеру значения области локальности, в рамках которой произвольные записи имеют производительность, аналогичную последовательным. Значение размера области локальности в устройствах наших дней обычно в пределах от 128кБ до 8МБ [4, 6].

Мы разбиваем вхождения в FD- дерево на категории двух видов, индексные вхождения и преграды (fetches - мосты - согласно охватывающей книге). На каждом уровне FD- дерева имеющиеся индексные вхождения и преграды организованы в восходящем порядке своих ключей.

В соответствии с установленным определением для внешней преграды, общее число внешних преград на уровне L_i равняется общему числу страниц на уровне L_i+1, т.е. |L_i+1|/f, где f равно общему числу вхождений в некой странице. Общее число внутренних преград на уровне L_i, по крайней мере, составляет |L_i|/f, так как каждая страница содержит по крайней мере одну внутреннюю преграду. Максимальное значение преград на уровне L_i, (|L_i| + |L_i+1|)/f должно быть меньше общего числа вхождений в L_i, достигая k < f - 1.

FD- дерево поддерживает пять общих операций запросов: поиск, вставку, слияние, удаление и обновление. За псевдокодом алгоритмов обратитесь к Приложению B.

Поиск. Некий поиск индекса в FD- дереве требует поиска на каждом уровне сверху донизу. Запрос может быть точечным поиском с неким предикатом эквивалентности, или поиском диапазона с предикатом диапазона.

Для выполнения точечного поиска по некому искомому ключу K мы вначале выполняем просмотр в своём головном дереве, точно так же как и в стандартном B⁺- дереве. Далее мы выполняем поиск на каждом уровне вслед за значением pid соответствующей преграды {моста}. Внутри некой страницы P на уровне L_i осуществляется двоичный поиск для поиска наилучшего ключа равного или меньшего чем K. Допустим, соответствующее вхождение e_i содержит такой ключ. Затем мы сканируем сортированный прогон справа налево пока не обнаружим некую преграду e_j. Поскольку все вхождения с ключами между e_i.key и e_j.key в нашем следующем уровне L_i+1 появляются на соответствующей странице e_j.pid (Инвариант 2), мы далее следуем по указателю e_j.pid на эту страницу для поиска вхождений на своём следующем уровне. Тем самым мы обходим всё дерево сверху вниз, следуя по pid принятых преград.

Так как некое фильтрующее вхождение вставляется в наше FD- дерево после какого- то удаления и превращает своё старое вхождение в некое фантомное вхождение, некий поиск может получить набор результата, содержащий как фильтрующее вхождение, так и соответствующее ему фантомное вхождение. Когда это имеет место, нам необходимо удалить из полученного в результате поиска набора фильтрующие вхождения и фантомные вхождения с тем же самым ключом и парой значения указателя.

В соответствии с Инвариантом 1 некий поиск по крайней мере может найти соответствующую преграду в самом первом разъёме любой страницы при сканировании такой страницы в обратном порядке. Тем самым, когда нет дубликатов, поиск сталкивается только с одной преградой на странице каждого уровня. Именно по этой причине мы ввели внутренние преграды. Когда данные скошены, соответствующие индексные вхождения между двумя последовательными внешними вхождениями, F_j и F_j+1 могут распространяться на множество страниц. Некому стартующему между F_j и F_j+1 сканированию необходимо пройти по множеству страниц для получения своей предыдущей преграды F_j. При наличии соответствующих внутренних преград такое сканирование останавливается соответствующим внутренними преградами в самом первом разъёме каждой из страниц.

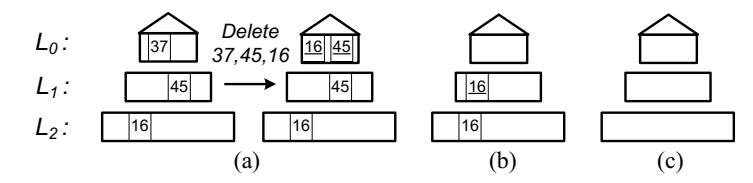
Рисунок B-2 b) иллюстрирует такой путь поиска ключа 81 (сплошная линия) и ключа 91 (пунктирная линия) в нашем примере FD- дерева с Рисунка B-2 a). На каждом уровне он находит соответствующую страницу из следующего уровня сортированных прогонов. При поиске 91 на уровне L₁, установленная на странице g преграда 88 препятствует данному сканированию в выборке страницы f при поиске соответствующей внешней преграды 71.

Поиск диапазона аналогичен точечному поиску за исключением того, что он способен выбирать на каждом уровне множество страниц. Получая значение преграды, удовлетворяющее значению предиката на своём текущем уровне L_i, нам становится известно об общем числе страниц, которое будет просканировано на соответствующем следующем уровне, L_i+1, прежде чем мы столкнёмся с преградой на этих страницах. Более того, эти страницы хранятся непрерывным образом. Данное свойство предоставляет нам возможность выборки точного числа соответствующих страниц со своего следующего уровня в некой операции ввода/ вывода применяя оптимизацию ввода/ вывода множества страниц (П3).

Вставка. некое новое вхождение изначально вставляется первым в своё головное дерево L₀. Когда общее число вхождений в этом головном дереве L₀ превосходит его ёмкость |L₀|, для L₀ и L₁ выполняется операция слияния с целью осуществления миграции всех вхождений L₀ на L₁. В результате, число произвольных записей ограничено в рамках установленного головного дерева, следуя принципу П2.

Слияние. Процесс слияния выполняется между двумя прилегающими уровнями когда меньший из них достигает предела своей ёмкости. Данная операция слияния последовательно два соответствующих входных потока и сочетает их в один сортированный прогон в непрерывных страницах. Вновь создаваемый уровень L_i состоит из всех индексных вхождений из L_i-1, а также всех индексных вхождений и внешних преград из L_i. Мы оставляем в L_i все внешние преграды, так как соответствующий уровень (L_i+1), на который указывают эти внешние вхождения не изменился. По мере необходимости конструируются соответствующие внутренние преграды L_i. В то же самое время перестраиваются соответствующие новые уровни L_j (0 ≤ j < i) для соответствующих конструируемых с вновь создаваемого уровня L_i внешних преград. То есть, получая два прилегающих уровня, L_i-1 и L_i, наш процесс слияния вырабатывает i + 1 новых сортированных прогонов для обновления всех уровней с L₀ до L_i. Если такой получаемый новый уровень L_i исчерпывает свою ёмкость, сливаются L_i и L_i+1. Этот процесс продолжается пока самый большой из двух вновь вырабатываемых уровней не перестанет исчерпывать свою ёмкость.

Данная операция слияния вовлекает в свой процесс только последовательные чтения и записи, тем самым мы успешно преобразуем свои произвольные записи вставки в последовательные считывания и записи, следуя своему принципу проектирования П1. Мы и далее оптимизируем производительнсоть своих операций ввода/ вывода применяя оптимизацию ввода/ вывода множества страниц следуя принципу П3. Так как страницы на каждом уровне FD- дерева хранятся непрерывным образом на соответствующем флэш- дискемы выполняем выборку множества страниц единым запросом ввода/ вывода. Аналогично, так как заново сгенерированные сортированные прогоны записываются последовательно, мы также записываем множество страниц единым запросом. Подходящее число страниц в неком запросе ввода/ вывода устанавливается равным размеру единицы доступа при котором скорость обмена шаблона последовательного доступа достигает максимального значения.

Удаление. Некое удаление в FD- дереве обрабатывается каким- то аналогичным вставке методом: оно сначала выполняется в установленном головном дереве, а затем мигрирует на свои нижние уровни по мере возникновения слияний. Такая схема логарифмического удаления снижает амортизационные расходы. Отметим, что известный метод ленивого удаления, широко используемый в жёстких дисках, на которых основывается индексация, который помечает некое вхождение как неверное, не эффективен для флеш SSD, так как операция пометки это небольшая произвольная запись.

Самый первый шаг состоит в выполнении удаления в имеющемся головном дереве L₀, так как произвольные записи в нашем головном дереве ограничены пространством и очень эффективны. Затем, мы выполняем удаление на всех прочих уровнях вставляя особое вхождение с названием фильтрующего вхождения. Такое подлежащее удалению вхождение далее становится фантомным вхождением и оставляется нетронутым. В частности, мы вначале выполняем в своём FD- дереве поиск примеяя соответствующий предикат для этого удаления. Такой поиск выявляет все подлежащие удалению индексные вхождения. Новые вхождения (фильтрующие вхождения) с тем же самым ключом и значением указателя что и эти вхождения вставляются в наше FD- дерево. Собственно реальное удаление осуществляется при операции слияния когда фильтрующие вхождения встречают свои соответствующие фантомные вхождения.

В процессе такого слияния в пакете выполняется физическое удаление. Когда некое фильтрующее вхождение достигает своего соответствующего фантомного вхождения, оба вхождения отвергаются и не будут более появляться в получаемом результате слияния. Таким образом и выполняется физическое удаление. Обратите внимание, что благодаря обработке фильтрующих вхождений и их фантомных вхождений, вновь вырабатываемый сортированный прогон может быть меньше старого.

Объём накладных расходов пространства фильтрующих и фантомных вхождений низок. Поскольку самый нижний уровень L_i-1 не содержит никаких фильтрующих или фантомных вхождений, эти вхождения в худшем случае занимают все уровни кроме самого нижнего, чей общий размер всего лишь около 1 / k всего индексного пространства. Так как k обычно велико, фильтрующие и фантомные вхождения оказывают низкое воздействие на производительность.

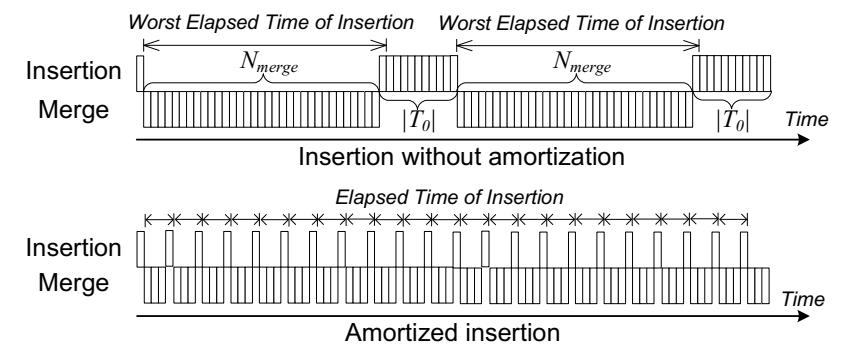
Рисунок B-3 иллюстрирует некий пример такого процесса удаления. Мы помечаем свои фильтрующие вхождения сплошным подчёркиванием. На Рисунке B-3 a) мы удаляем свои индексные вхождения 37 для L₀, 45 для L₁ и 16 для L₂. Поскольку вхождение 37 находится в нашем головном дереве L₀, оно удаляется непосредственно из L₀. Соответствующие фильтрующие вхождения 45 и 16 вставляются в наше головное дерево. По мере выполнения прочих вставок и удалений, наше головное дерево постепенно становится большим. Когда оно заполняется и выполняется слияние L₀ и L₁, как это показано на Рисунке B-3 b), фильтрующее вхождение 45 сталкивается со своим фантомным вхождением и оба вхождения отвергаются. При вставке большего числа вхождений в значения индексов и когда происходит слияние между L₁ и L₂, как это показано на Рисунке B-3 c), отвергаются фильтрующее вхождение 16 и соответствующее ему фантомное вхождение.

Обновление. Операция обновления реализуется как некое удаление для старого значения со следующей за ним вставкой.

Хотя логарифмический метод и снижает амортизированную стоимость вставок в FD- дерево, в наихудшем случае стоимость всё ещё остаётся высокой. В наихудшем случае у всех отсортированных прогонов заканчивается их ёмкость после одиночной операции вставки и всё FD- дерево должно быть целеком переписано. Этот процесс может иметь результатом некое недопустимое время отклика. В результате, мы предлагаем некую простую и действенную схему решения данной проблемы. В качестве некого образца мы выбираем процесс возврата отчуждения для вставок, так как удаления и обновления обрабатываются аналогично.

Рисунок B-4 демонстрирует основную идею возврата отчуждений вставок в FD- дереве, которая состоит в перекрытии процесса выполнения операций вставок и слияния. В частности, получая под слияние N_merge вхождений, мы делим эти N_merge вхождений на |L₀| разделов и со временем комбинируем вхождения в неком разделе после выполнения некой вставки. В результате общая затратная стоимость соответствующей операции слияния возмещается |L₀| операциями вставок. Тем самым наихудшее время на вставки уменьшается примерно на множитель |L₀|, причём средняя стоимость остаётся неизменной.

Чтобы перекрывать время исполнения вставок и слияния мы поддерживаем два головных дерева. Как только некое головное дерево L₀ наполняется, новые вхождения вставляются в другой экземпляр, то есть во временное головное дерево L'₀, в то время как само слияние выполняется для L₀. Этот процесс слияния аналогичен тому, что мы описали в разделе 3.3, за исключением того что внешние преграды {мосты} из соответствующих нижних уровней вставляются в L'₀ одна за другой вместо выполнения пакетом. После того как данное слияние завершено, L'₀ уже был заполнен и все врешние преграды уже были вставлены в L'₀. При возврате отчуждений после завершения слияния мы меняем местми L₀ и L'₀ для последующих вставок и слияний.

С помощью возврата отчуждений запросы поиска индекса могут продолжаться даже в процессе слияния. Так как первоначальное FD- дерево (L₀ ~ L_l-1) содержит все первоначальные вхождения вставленными до самой операции слияния, а временное головное дерево L'₀ хранит все вновь созданные вхождения, мы можем осуществлять просмотр как в своём первоначальном FD- дереве (L₀ ~ L_l-1), так и в нашем временном головном дереве L'₀. Значение размера временного головного дерева (T'₀) настолько мало, что скорее всего умещается в памяти и значение накладных расходов производительности поиска с возвратом отчуждений незначительно.