Глава 7. Понижающие операторы в процессах

Вот перечень предварительных требований для данной главы:

Будучи опытным программистом, вы несомненно сталкивались с ситуациями, когда вам необходимо было вычислять значения суммы или произведения всех чисел в каком- то массиве, либо вычислять результат применения оператора AND ко всем булевым элементам в некотором массиве чтобы определить имеется ли какое- нибудь ложное значение в этом массиве. Когда берётся некое множество или массив элементов и осуществляется некий вид вычислений для возврата всего лишь одного значения, это именуются понижающими операторами (свёрткой).

Не все операторы из математики или информатики являются понижающими операторами. На самом деле, даже если некоторый оператор и способен сводить некий массив элементов к какому- то отдельному элементу, всё ещё нет гарантии, что он является понижающим оператором. Некий оператор является понижающим оператором, если он удовлетворяет следующим условиям:

Первое условие определяет значение фразы "понижающих операций", поскольку все элементы получаемого на вход массива подлежат комбинированию и сведению к одному отдельному значению. Однако второе условие, по существу, определяет одновременную обработку и параллелизм. Оно требует возможности подразделения собственно вычисления любого понижающего оператора на частичные вычисления меньшего размера.

Для начала давайте рассмотрим самые распространённые понижающие операторы: сложения. К примеру, рассмотрим определённый входной массив [1, 4, 8, 3, 2, 5] - сумма всех элементов этого массива является такой:

1 + 4 + 8 + 3 + 2 + 5
= ((((1 + 4) + 8) + 3) + 2) + 5
= (((5 + 8) + 3) + 2) + 5
= ((13 + 3) + 2) + 5
= (16 + 2) + 5
= 18 + 5
= 23
 	   

В своём предыдущем вычислении мы свернули значения чисел в своём массиве в их сумму, 23, причём неким последовательным образом. Другими словами, мы обошли все без исключения элементы своего массива с самого начала до его конца и добавляли их в текущее значение суммы. А теперь, мы знаем, что сложение является коммуникативным и ассоциативным оператором, что означает: a + b = b + a и (a + b) + c = a + (b + c).

Тем самым, мы можем осуществить своё предыдущее вычисление более эффективным образом разбивая своё суммирование на суммы меньшего размера:

1 + 4 + 8 + 3 + 2 + 5
= ((1 + 4) + (8 + 3)) + (2 + 5)
= (5 + 11) + 7
= 16 + 7
= 23
 	   

Эта техника находится в сердцевине применения одновременной обработки и параллелизма (в частности, множественности процессов) в некотором понижающем операторе. Разбивая всю задачу на подзадачи меньшего размера, множество процессов может осуществлять такие вычисления меньшего размера одновременно, причём вся система в целом может достигать окончательного результата намного быстрее.

По той же самой причине, обсуждаемые свойства коммуникативности и ассоциативности рассматриваются как некий эквивалент требований для какого- то оператора свёртки, который мы обсудили ранее. Другими словами, наш оператор ○ является понижающим оператором (оператором свёртки) тогда и только тогда, когда он коммутативен и ассоциативен. В частности так:

Здесь a, b и c являются элементами входного массива.

Таким образом, если некий оператор является оператором свёртки, он обязан быть коммуникативным и ассоциативным и, тем самым, иметь возможность разбивать некую большую задачу на меньшие, более управляемые подзадачи, которые могут вычисляться более действенно при помощи множества процессов.

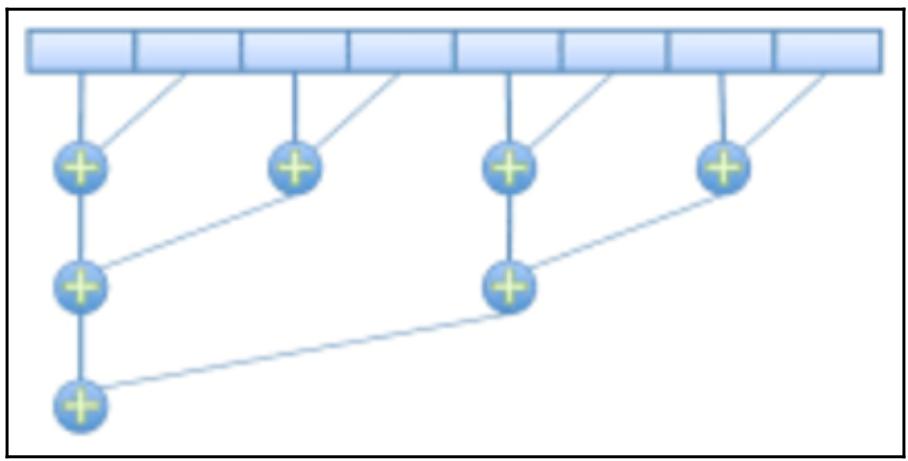
До сих пор мы видели, что сложение является одним из примеров операции свёртки. Для выполнения сложения в качестве понижающей операции, мы для начала делим свои элементы нашего входного массива на группы по два, причём каждая из них является одной из наших подзадач. Затем мы добавляем сложение в каждой из групп, получаем результаты из всех групп и выполняем их деление на группы снова.

Этот процесс продолжается пока мы не достигаем одного отдельного числа. Данный процесс следует некоторой модели, именуемой двоичным деревом свёртки, который применяет группирование по два для создания подзадач:

В своём предыдущем примере с заданным массивом [1, 4, 8, 3, 2, 5], после разделения всех чисел на три различные группы из двух чисел (1 и 4, 8 и 3, 2 и 5), мы воспользовались тремя отдельными процессами для сложения пар чисел воедино. Затем мы получили соответствующий массив [5, 11, 7], который мы применили для одного процесса чтобы получить [16, 7] и вновь другой процесс для окончательного получения 23. Таким образом, при трёх или более ЦПУ некий оператор сложения шести элементов может быть выполнен за log₂6 = 3 шага вместо пяти шагов при последовательном сложении.

Другими распространёнными операторами свёртки являются умножение и логическое И. Например, свёртка того же самого массива чисел [1, 4, 8, 3, 2, 5] при помощи умножения в качестве понижающего оператора может быть выполнена следующим образом:

1 x 4 x 8 x 3 x 2 x 5
= ((1 x 4) x (8 x 3)) x (2 x 5)
= (4 x 24) x 10
= 96 x 10
= 960
 	   

Для свёртки некоторого массива Булевых значений, скажем, [True, False, False, True], с применением соответствующего логического оператора AND, мы можем выполнить следующее:

True AND False AND False AND True
= (True AND False) AND (False AND True)
= False AND False
= False
 	   

Неким не подходящим примером операторов свёртки является функция степени, поскольку изменение заданного порядка вычислений изменило бы окончательный получаемый результат (то есть эта функция не является коммуникативной). Например, последовательная свёртка заданного массива [2, 1, 2] даёт нам следующее:

2 ^ 1 ^ 2 = 2 ^ (1 ^ 2) = 2 ^ 1 = 2
 	   

После того как мы изменим установленный порядок операций, мы получим:

(2 ^ 1) ^ 2 = 2 ^ 2 = 4
 	   

Мы достигаем различных результатов, таким образом, операция возведения в степень не является операцией свёртки.

Как мы уже упоминали ранее, благодаря свойствам коммуникативности и ассоциативности, операторы свёртки могут получать создание и обработку своих задач независимо и именно таким образом может применяться одновременная обработка. Чтобы по настоящему понять как понижающий оператор применяет одновременную обработку, давайте попробуем реализовать некий одновременный оператор свёртки со множеством процессов с нуля - в частности, обсуждавшийся оператор сложения.

Аналогично тому, что мы наблюдали в своей предыдущей главе, в данном примере мы воспользуемся некоей очередью задач и очередью результатов для оформления своего межпроцессного взаимодействия. В частности, наша программа будет хранить все свои числа из входного массива в определённой очереди задач как индивидуальные задачи. По мере того как наши потребители (индивидуальные процессы) исполняются, они дважды вызывают get() для своей очереди задач чтобы получить числа задач (за исключением неких граничных ситуаций, когда нет чисел вовсе или остаётся только одно число в такой очереди задач), складывает их вместе, и помещает результат в очередь результатов.

Аналогично сложению пар вместе, как мы это делали в своём предыдущем разделе, после того как наши процессы выполнят итерацию по своей очереди задач один раз и поместят сложенные пары чисел задач в свою очередь результатов, общее число элементов в нашем входном массиве уменьшается наполовину. К примеру, наш входной массив [1, 4, 8, 3, 2, 5] превратится в [5, 11, 7].

Теперь наша программа назначает своей очередью задач очередь результатов (скажем, в нашем случае, это теперь [5, 11, 7] является новой очередью задач), а наши процессы продолжат проистекать и складывать пары чисел воедино для создания новой очереди результатов, которая в своё время превратится в следующую очередь задач. Этот процесс повторяет себя пока очередь результата не будет содержать только один элемент, так как мы знаем, что такое единственное число является суммой всех чисел нашего первоначального массива на входе.

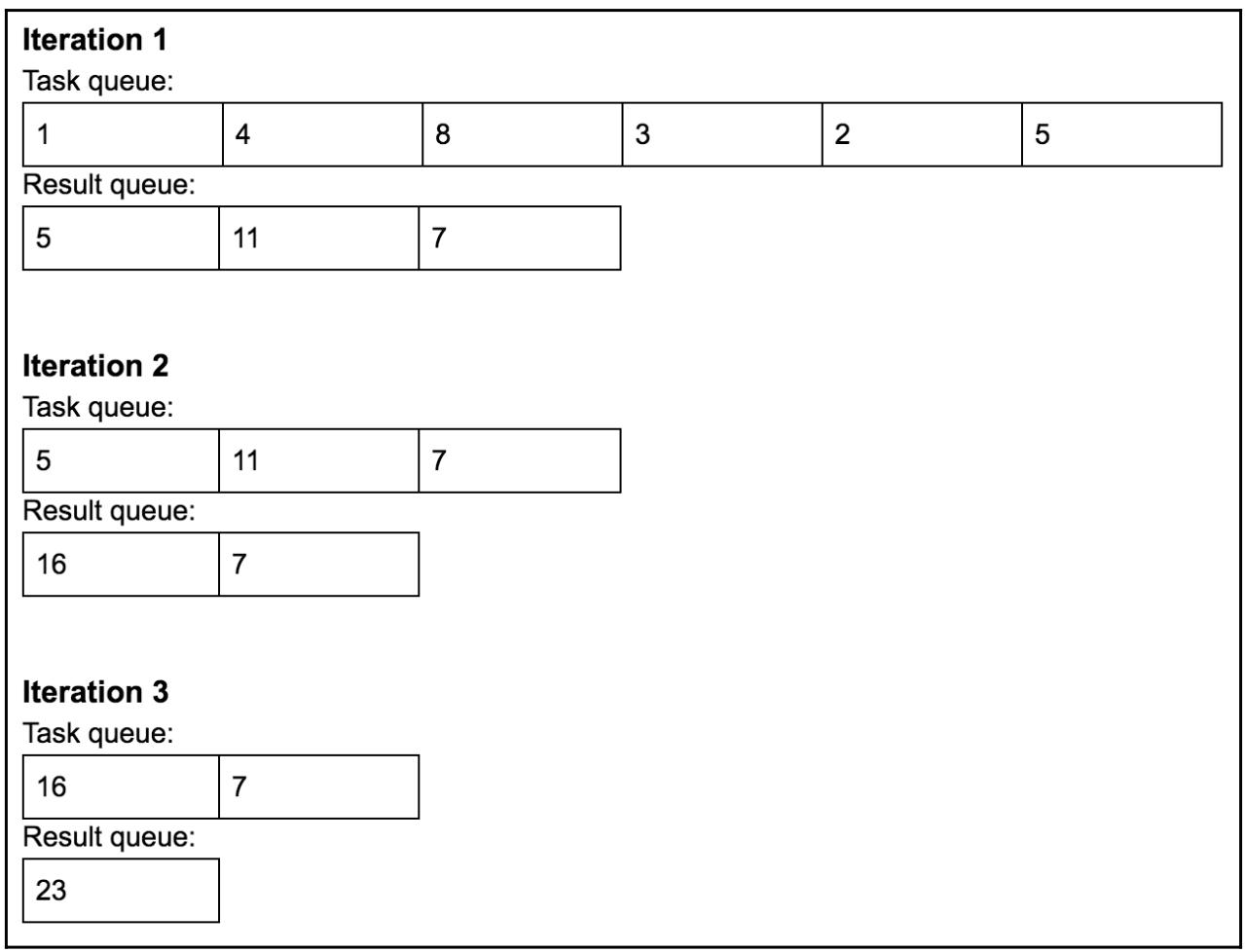
Наша следующая схема отображает соответствующие изменения в своей очереди задач и очереди результатов при каждой итерации обработки своего входного массива [1, 4, 8, 3, 2, 5]; наш процесс останавливается когда наша результирующая очередь содержит только одно число [23]:

Давайте рассмотрим свой класс ReductionConsumer из нашего файла Chapter07/example1.py:

# Chapter07/example1.py

class ReductionConsumer(multiprocessing.Process):

    def __init__(self, task_queue, result_queue):
        multiprocessing.Process.__init__(self)
        self.task_queue = task_queue
        self.result_queue = result_queue

    def run(self):
        pname = self.name
        print('Using process %s...' % pname)

        while True:
            num1 = self.task_queue.get()
            if num1 is None:
                print('Exiting process %s.' % pname)
                self.task_queue.task_done()
                break

            self.task_queue.task_done()
            num2 = self.task_queue.get()
            if num2 is None:
                print('Reaching the end with process %s and number 
                      %i.' % (pname, num1))
                self.task_queue.task_done()
                self.result_queue.put(num1)
                break

            print('Running process %s on numbers %i and %i.' % (
                    pname, num1, num2))
            self.task_queue.task_done()
            self.result_queue.put(num1 + num2)
 	   

Мы реализуем свой класс ReductionConsumer переписав имеющийся класс multiprocessing.Process. Этот класс потребителя при инициализации получает некую очередь задач и какую- то очередь результатов и обрабатывает логику своего процесса потребителя в данной программе, которая дважды вызывает get() для своей очереди задач чтобы получить два числа из этой очереди и складывает их сумму в своей очереди результатов.

При выполнении этого наш класс ReductionConsumer также обрабатывает случаи при которых нет чисел вовсе или остаётся только одно число в очереди задач (то есть когда переменная num1 или num2 содержит None, что, как мы знаем по своей предыдущей главе, является тем, что мы применяем в качестве своей ядовитой пилюли).

Кроме того, повторный вызов такого класса JoinableQueue из модуля multiprocessing применяется для реализации наших очередей задач и именно он требует вызова соответствующей функции task_done() после каждого вызова функции ReductionConsumer get(), в противном случае последующая функция join(), которую мы вызываем позднее в своей очереди задач осуществляет неограниченное блокирование. Итак, в том случае, когда наш процесс потребителя дважды вызывает get(), в текущей очереди задач важно дважды вызвать task_done(), а когда get() вызывается один раз (в том случае, когда самое первое число является ядовитой пилюлей), тогда нам следует вызывать task_done() только один раз. Именно это является наиболее сложным подлежащим рассмотрению приёмом при работе с многопроцессными программами, который обеспечивает межпроцессное взаимодействие.

Для обработки различных процессов потребителей и их координации, а также для манипуляции соответствующими очередями задач и результатов после каждой итерации у нас имеется отдельная функция с названием reduce_sum():

def reduce_sum(array):
    tasks = multiprocessing.JoinableQueue()
    results = multiprocessing.JoinableQueue()
    result_size = len(array)

    n_consumers = multiprocessing.cpu_count()

    for item in array:
        results.put(item)

    while result_size > 1:
        tasks = results
        results = multiprocessing.JoinableQueue()

        consumers = [ReductionConsumer(tasks, results) 
                     for i in range(n_consumers)]
        for consumer in consumers:
            consumer.start()

        for i in range(n_consumers):
            tasks.put(None)

        tasks.join()
        result_size = result_size // 2 + (result_size % 2)
        #print('-' * 40)

    return results.get()
 	   

Эта функция берёт некий список чисел Python для вычисления результирующей суммы его элементов. Помимо некоторой очереди задач и какой- то очереди результатов, данная функция также отслеживает другую переменную с названием result_size, которая указывает значение общего числа элементов в её текущей очереди результатов.

После инициализации её базовых переменных, эта функция порождает свои потребительские процессы для уменьшения своей текущей очереди задач внутри цикла while. После этого данная очередь задач получит соответствующие элементы такой очереди результатов и добавит дополнительные значения None в свою очередь для реализации техники ядовитой пилюли.

При каждой итерации также инициализируется некий новый пустой элемент очереди результата в виде объекта JoinableQueue - это отличается от нашего класса multiprocessing.Queue, который мы применяли для очереди результатов в своей предыдущей главе, так как мы будем назначать tasks = results в самом начале своей следующей итерации а наша очередь задач обязана быть неким объектом JoinableQueue.

В конце каждой итерации мы также обновляем текущее значение result_size посредством result_size = result_size // 2 + (result_size % 2). Здесь важно заметить, что хотя метод qsize() из нашего класса JoinableQueue потенциально является методом для отслеживания длины его объекта (то есть количества элементов в некотором объекте JoinableQueue), этот метод обычно рассматривается как являющийся не надёжным - он даже не реализован в операционных системах Unix.

Так как мы запросто можем предсказать как общее число остающихся численных значений из нашего входного массива будет изменяться после каждой итерации (это будет половина если значение - некое чётное число, в противном случае оно делится пополам нацело, а затем к полученному результату добавляется 1), мы можем отслеживать это число применяя некую отдельную переменную называемую result_size.

Относительно нашей основной программы для данного примера, мы просто передаём список Python в её функцию reduce_sum(). Здесь мы добавляем числа от 0 до 19:

my_array = [i for i in range(20)]

result = reduce_sum(my_array)
print('Final result: %i.' % result)
 	   

После запуска данного сценария ваш вывод должен походить на следующее:

> python example1.py
Using process ReductionConsumer-1...
Running process ReductionConsumer-1 on numbers 0 and 1.
Using process ReductionConsumer-2...
Running process ReductionConsumer-2 on numbers 2 and 3.
Using process ReductionConsumer-3...

[...Truncated for readability..]

Exiting process ReductionConsumer-17.
Exiting process ReductionConsumer-18.
Exiting process ReductionConsumer-19.
Using process ReductionConsumer-20...
Exiting process ReductionConsumer-20.
Final result: 190.
		

Коммуникативный и ассоциативный характер того как операторы свёртки обрабатывают свои данные делает возможной независимую обработку подзадач оператора и тем самым теснейшим образом связан с одновременной обработкой и параллелизмом. Вследствие этого различные темы параллельного программирования могут соотноситься с операторами свёртки, а применяя те же самые принципы оператора свёртки, относящиеся к этим темам задачи могут быть сделаны более понятными интуитивно и выполняться более действенно.

Как мы уже видели, операторы сложения и умножения являются понижающими операторами. Более расширенно, задачи перемалывания чисел, которые обычно вовлекают коммуникативные и ассоциативные операторы являются первейшими кандидатами на использование одновременной обработки и параллелизма. Это в особенности справедливо для самого знаменитого и вероятно одного из наиболее применяемых модулей Python - NumPy, код которого реализован с тем чтобы быть распараллеленным настолько, насколько это возможно.

Более того, применение логических операторов AND, OR или XOR к некому массиву Булевых значений работает аналогично операторам свёртки. Некоторые приложения из реальной жизни для одновременной обработки побитовых понижающих операторов включают следующее:

При реализации операторов свёртки со множеством процессов следует соблюдать осторожность, в особенности если ваша программа применяет очереди задач и очереди результатов для оснащения взаимодействия между имеющимися процессами пользователя.

Операции различных реальных задач напоминают операторы свёртки, а применение совместной обработки и параллелизма для этих задач может значительно повысить эффективность а, следовательно, и производительность обрабатывающих их программ. Поэтому важно быть в состоянии выявлять такие задачи и возвращаться обратно к понятию понижающих операторов для реализации их решений.

В своей следующей главе мы обсудим особенное приложение из реального мира для программ со множеством процессов в Python: обработку изображений. Мы рассмотрим основные идеи обработки изображений и то, как параллелизм, в частности многопроцессорность, может быть применён к приложениям обработки изображений.

Для получения дополнительных сведений вы можете воспользоваться следующими ссылками: