Глава 8. Неоднородные вычисления

На протяжении многих лет поиск наилучшей производительности для всё более сложных вычислений привёл к принятию новых методов применения компьютеров. Один из таких способов имеет название неоднородных вычислений (гетерогенных вычислений), который имеет целью взаимодействие с различными (или гетерогенными) процессорами таким образом, чтобы получать преимущества (в частности) в отношении промежуточной вычислительной мощности.

В этом контексте, тот процессор, в котором запущена основная программа (как правило, ЦПУ) именуется хостом, в то время как имеющиеся сопроцессоры (например, GPU) имеют название устройств. Эти последние обычно физически обособлены в своём хосте и управляют своим собственным пространством памяти, которое также обособлено от памяти хоста.

В частности, следуя за значительным спросом на рынке, такие GPU превратились в процессор с высокой параллельностью, преобразовав графический процессор из устройства построения графики в устройства для параллельных и интенсивных вычислений общего назначения.

В действительности применение GPU для задач, отличных от построения графического изображения на экране и имеет название неоднородных вычислений.

Наконец, задача достойного программирования GPU состоит в том, чтобы максимально применять высокий уровень параллелизма и математических возможностей, предлагаемых такими графическими картами, сводя к минимуму все предоставляемые ею недостатки, например, задержку физического соединения между самим хостом и устройством.

Некий GPU является специализированным процессором/ ядром для векторной обработки графических данных при построении изображения из примитивов многоугольников. Основная задача хорошнй программы GPU состоит в максимальном применении предлагаемого графическими картами высочайшего уровня параллелизма и математических возможностей при минимизации всех имеющихся у неё недостатков, таких как задержка в физическом соединении между основным хостом и его устройством.

GPU отличается высокой степенью параллельности строения, что делает возможным эффективную работу с большими наборами данных. Эти свойства сочетаются с быстрыми улучшениями в аппаратной производительности программ, привнося особое внимание всего научного мира к возможности применения GPU для целей, отличающихся от построения изображений.

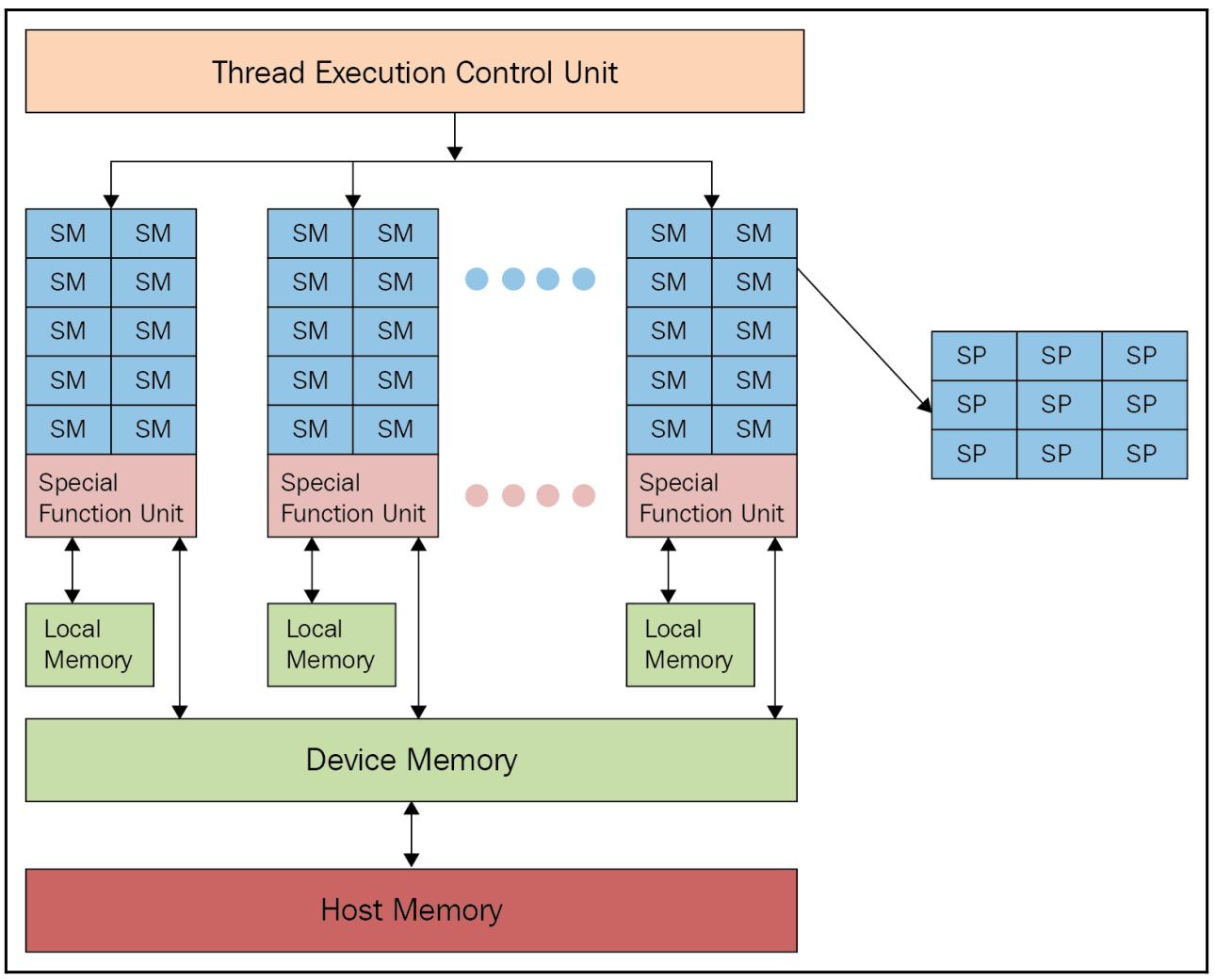
Некий GPU (см. следующую схему) состоит из определённого числа вычислительных устройств, носящих название Потоковых мультипроцессоров (SM, Streaming Multiprocessors), которые являют собой самый первый уровень параллелизма. На практике каждый SM работает одновременно и независимо от прочих.

Каждый SM делится на некую группу Потоковых процессоров (SP, Streaming Processors), обладающих неким ядром, способным последовательно выполнять некий поток. Такой SP представляет наименьший элемент логики выполнения и самый тонкий уровень параллельности.

Для наилучшего программирования такого типа архитектуры нам требуется представить программирование GPU, которое мы и описываем в следующем разделе.

Графические процессоры непрерывно улучшают свои программные возможности. На практике их набор инструкций был расширен для предоставления возможности выполнения большего числа задач.

В наши дни GPU способен выполнять классические инструкции ЦПУ, такие как циклы и условия , доступ к памяти и вычисления с плавающей точкой. Два основных производителя дискретных видео карт - NVIDIA и AMD - разработали собственные архитектуры GPU, снабжая разработчиков соответствующими средами разработки, которые позволяют программировать на различных языках программирования, включая Python. {Прим. пер.: во второй половине ноября 2019 года мы намерены выложить в Дополнении к этому переводу описание интерфейса Python для нового процессора Fujitsu (DLU), выпускаемого ими в сотрудничестве с Intel 5 ноября 2019.}

В настоящее время разработчики обладают ценными инструментами для написания программного обеспечения, которое применяет GPU в не связанном с графикой контексте. Среди основных сред разработки для неоднородных вычислений у нас имеются CUDA и OpenCL.

Давайте рассмотрим их подробнее.

CUDA является частной аппаратной архитектурой nVIDIA, которая также снабдила своим названием и связанную с ней среду разработки. В наши дни CUDA обладает пулом из сотен тысяч активных разработчиков, которые демонстрируют растущий интерес со стороны разработчиков к данной технологии в среде параллельного программирования.

CUDA предлагает расширения для наиболее применяемых языков применяемых в программировании, в том числе и Python. Наиболее хорошо известными расширениями CUDA Python являются:

В последующих разделах мы рассмотрим их подробнее.

Вторым главным действующим лицом в параллельных вычислениях выступает OpenCL, который (в отличие от своего аналога nVIDIA) является открытым стандартом и может применяться не только с графическими процессорами разных производителей, но и с микропроцессорами разных типов.

Тем не менее, OpenCL является более полным и универсальным решением, пока не обладающим такой зрелости и простоты применения как CUDA.

Расширением OpenCL в Python выступает PyOpenCL.

В наших последующих разделах будут проанализированы модели программирования CUDA и OpenCL в их расширениях Python и они будут сопровождены некоторыми занятными примерами использования.

PyCUDA это библиотека привязок, обеспечивающая доступ к API Python CUDA от Андреаса Клёкнера. Основные функции содержат автоматическую очистку, которая привязана к времени жизни объектов, что предотвращает утечки памяти, удобную абстракцию поверх модулей и буферов, полный доступ к драйверу и встроенную обработку ошибок.

Данный продукт является открытым исходным кодом с лицензией MIT, его документация очень ясная, к тому же множество находящихся в открытом доступе исходных кодов могут оказать содействие и поддержку. Основная цель PyCUDA состоит в том, чтобы позволить разработчику вызывать CUDA с минимумом абстракций Python и также поддерживать метапрограммирование и шаблоны CUDA.

Для установки PyCUDA, будьте любезны следовать инструкциям домашней страницы Андреаса Клёкнера.

Наш следующий пример программирования имеет двойную функцию:

Давайте рассмотрим следующие шаги:

Всё исполнение достаточно незатейливое. В самой первой строке кода импортируется pycuda.driver, а затем и инициализируется:

import pycuda.driver as drv
drv.init()
	   

Этот модуль pycuda.driver выставляет уровень драйвера для интерфейса программирования CUDA, что более удобно нежели интерфейс программирования времени исполнения C CUDA, к тому же он обладает рядом функциональных возможностей, которые не представлены в интерфейсе времени выполнения.

Затем он обходит в цикле значение функции drv.Device.count(), причём для каждой карты GPU выводятся на печать название этой карты и её основные характеристики (вычислительные возможности и общий объём памяти):

print ("Device #%d: %s" % (ordinal, dev.name()))
print ("Compute Capability: %d.%d" % dev.compute_capability())
print ("Total Memory: %s KB" % (dev.total_memory()//(1024)))
	   

Выполняем следующий код:

C:\> python dealingWithPycuda.py
		

После его выполнения на экране будут отображены все установленные GPU, примерно как в следующем образце:

1 device(s) found.
Device #0: GeForce GT 240
Compute Capability: 1.2
Total Memory: 1048576 KB
		

Модель программирования CUDA (а следовательно и PyCUDA, которая является обёрткой Python) реализуется через особые расширения стандартной библиотеки, написанной на языке программирования С. Эти расширения были созданы просто как вызовы функции из стандартной библиотеки C, делая возможным простой подход к модели неоднородного программирования, которая содержит код и для своего хоста, и для устройства. Собственно управление такими двумя логическими частями выполняется компилятором nvcc.

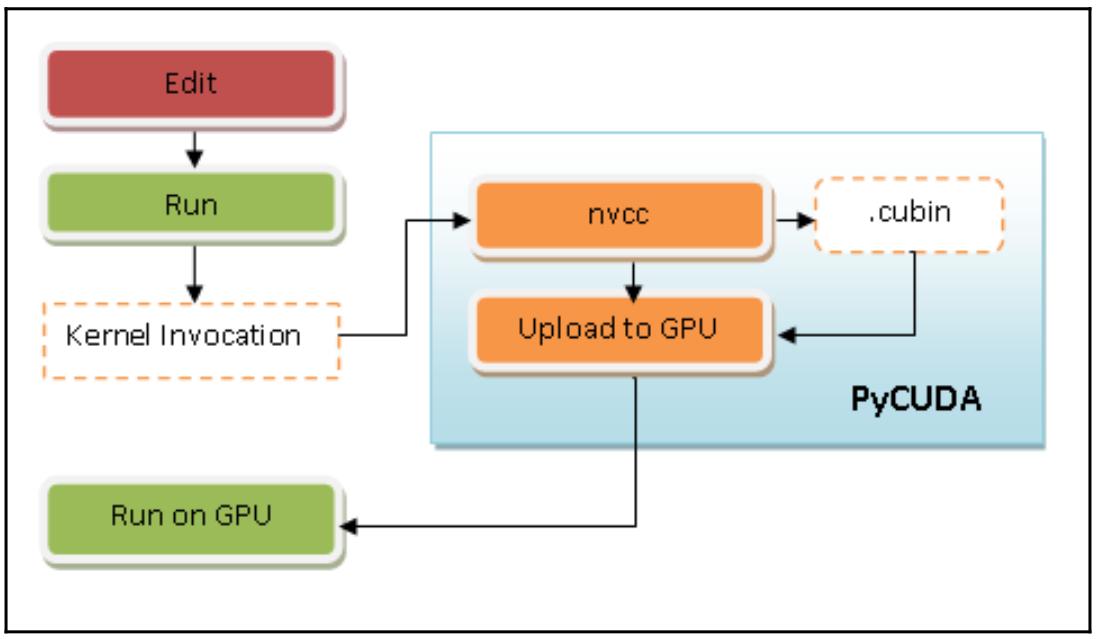
Вот краткое описание того как это работает:

Все предыдущие шаги выполняются со стороны PyCUDA в процессе выполнения с неким ростом в нагрузке времени исполнения по сравнению с приложением CUDA.

Модель программирования CUDA (а следовательно и PyCUDA) разработана для того чтобы соединить программное приложение ЦПУ и GPU для выполнения имеющейся последовательной части в установленном ЦПУ, а той части, которая может выполняться параллельно, в присутствующем GPU. К сожалению, наш компьютер не достаточно сообразителен чтобы разбираться в том как автономно распределять полученный код, а потому именно разработчик сверху должен указывать какие части следует выполнять в ЦПУ, а какие в GPU.

На практике приложение CUDA составляется из неких последовательных компонентов, которые выполняются ЦПУ системы или хоста, либо параллельных компонентов, носящих названия ядер (kernels), которые исполняются вместо этого GPU или устройством.

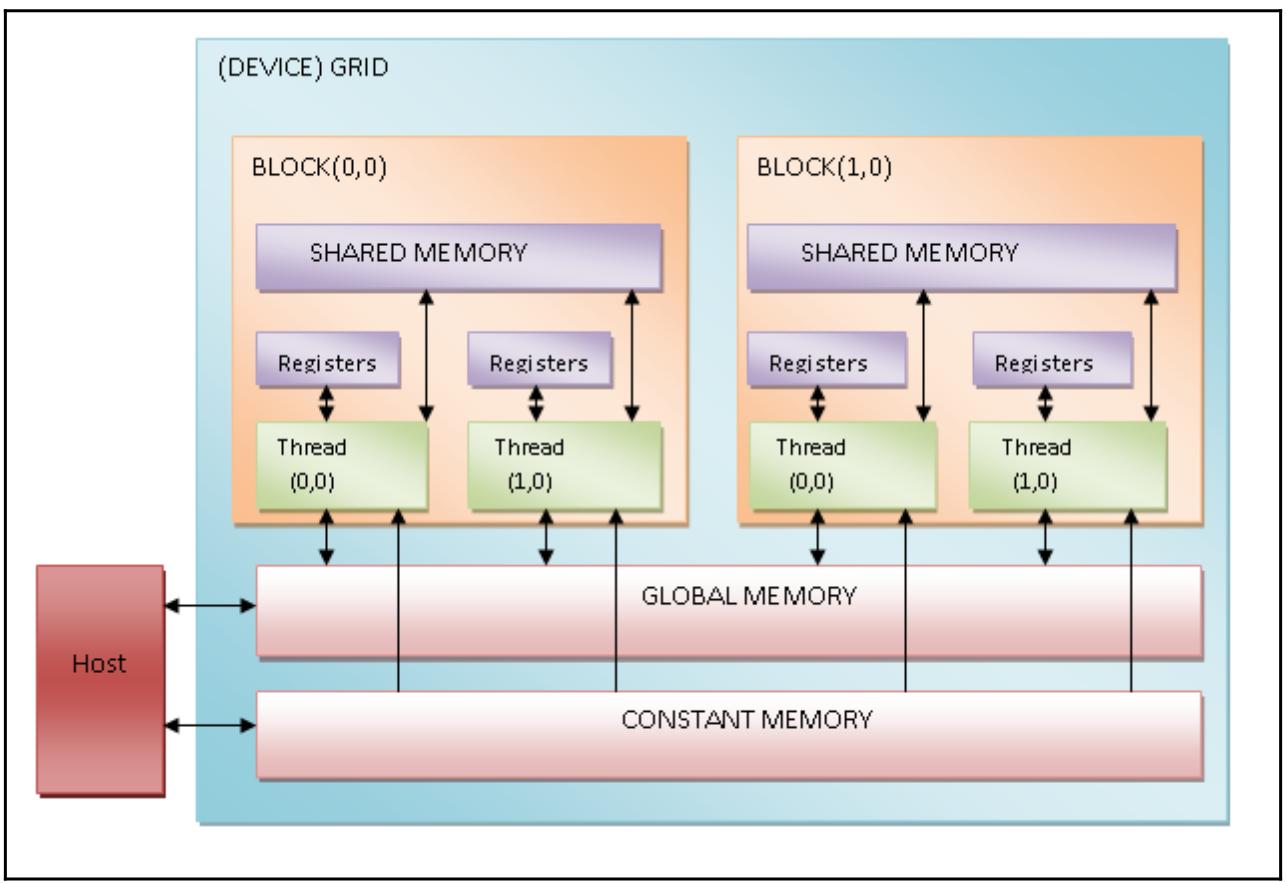
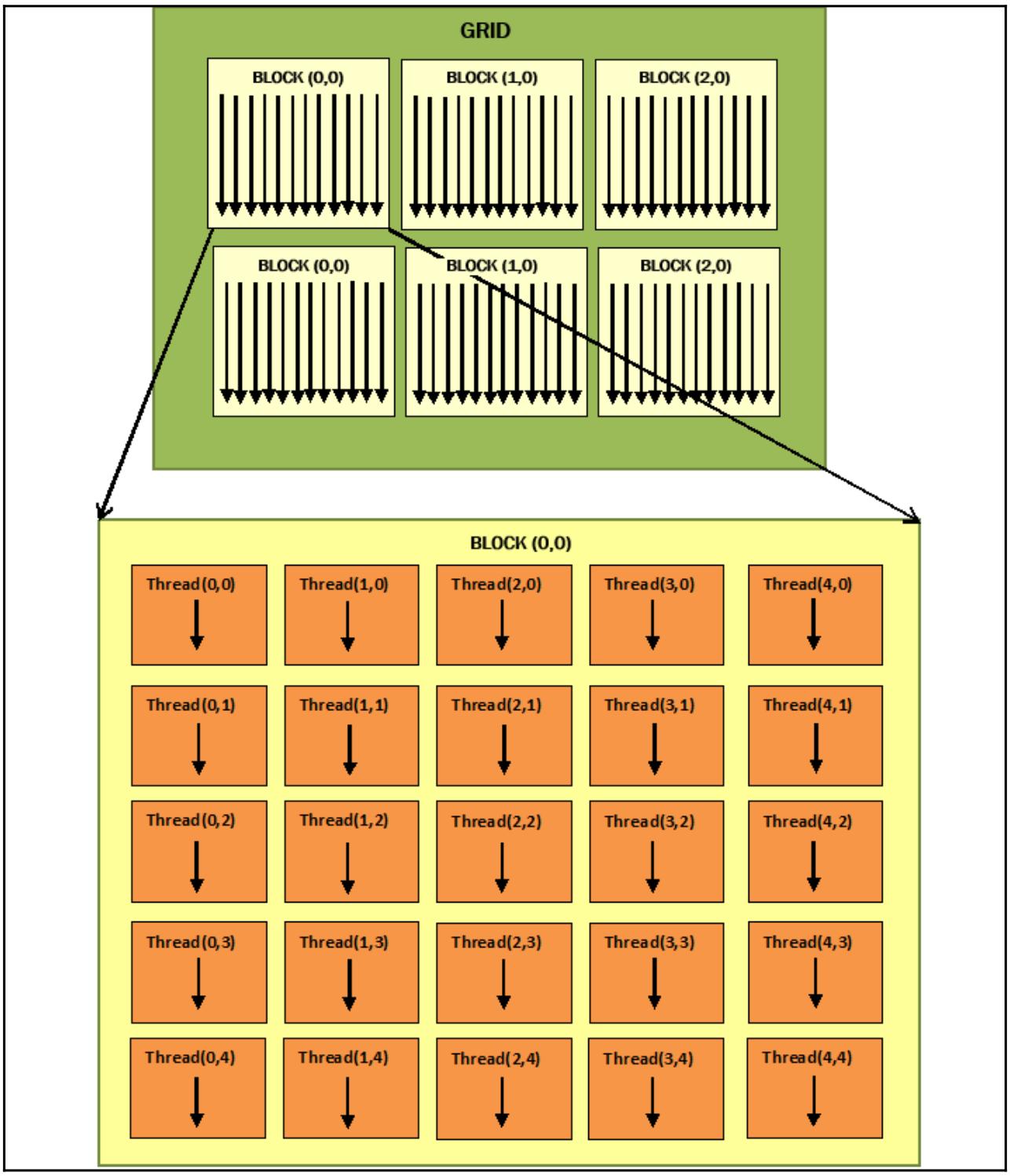
Некое ядро определяется как решётка (сетка, grid) и в свою очередь может подвергаться декомпозиции на блоки, которые последовательно назначаются различным мультипроцессорам, тем самым реализуя параллелизм крупной грануляции (coarse-grained parallelism). Внутри этих блоков присутствуют основополагающие вычислительные элементы, потоки, с очень тонкой степенью параллельной грануляции (fine parallel granularity). некий поток может относиться только к одному блоку и идентифицироваться неким уникальным индексом для блоков и трёхмерными индексами для потоков. В них имеющиеся ядра выполняются последовательно. Блоки же и потоки, в свою очередь, выполняются параллельно. Общее число запущенных (параллельно) потоков зависит от их организации в блоки, а также от их запросов в плане ресурсов в соответствии с теми ресурсами, которые доступны в данном устройстве.

Наши блоки разрабатываются с тем, чтобы гарантировать масштабирование. На практике, когда у вас имеется архитектура с двумя процессорами и другая с четырьмя, тогда приложение GPU может выполняться в обеих архитектурах с различными временами и уровнями параллельности.

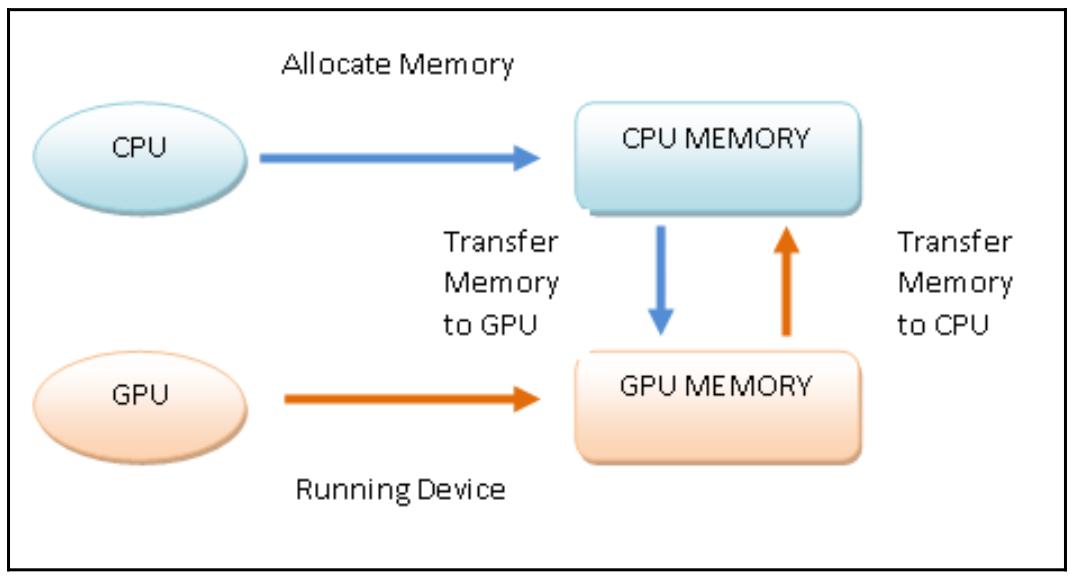
Для выполнения некой неоднородной программы в соответствии с рассматриваемой моделью программирования PyCUDA, оно строится следующим образом:

Следующая схема отображает обсуждаемый поток выполнения программы в соответствии с моделью программирования PyCUDA:

В своём следующем примере мы пройдёмся по конкретному примеру данной методологии программирования чтобы следовать порядку построения приложений PyCUDA.

Для демонстрации модели программирования PyCUDA мы рассмотрим задачу дублирования всех элементов в матрице 5 х 5:

Давайте начнём с просмотра импортируемых нами библиотек:

import PyCUDA.driver as CUDA
import PyCUDA.autoinit
from PyCUDA.compiler import SourceModule
	   

В частности, наш импорт autoinit автоматически определяет какой именно GPU в нашей системе доступен для работы, в то время как SourceModule является директивой для того компилятора nVidia (nvcc), который позволит нам указать неободимые объекты, подлежащие компиляции и выгрузке в соответствующее устройство.

Далее при помощи библиотеки numpy мы строим свою входную матрицу 5 х 5:

import numpy
a = numpy.random.randn(5,5)
	   

В данном случае все элементы нашей матрицы преобразуются в режиме одинарной точности (так как та графическая карта, на которой исполняется данный пример, поддерживает только одинарную точность):

a = a.astype(numpy.float32)
	   

Далее мы копируем свой массив из основного хоста в имеющееся устройство при помощи следующих двух операций:

a_gpu = CUDA.mem_alloc(a.nbytes)
CUDA.memcpy_htod(a_gpu, a)
	   

Обратите внимание, что и само устройство и его хост могут никогда не взаимодействовать в процессе самого исполнения некой функции ядра. По этой причине для параллельного исполнения такой функции ядра в этом устройстве все те данные, которые относятся к самой функции ядра должны также присутствовать в памяти вычислительного устройства.

Также следует обратить внимание что наша матрица a_gpu линеаризована, то есть имеет одно измерение, а следовательно должна обрабатываться именно так.

Более того, все эти действия не требуют вызовов ядра. Это означает, что они напрямую выполняются самим хостом.

Логический элемент SourceModule делает возможным определение нашей функции ядра doubleMatrix. __global__, который выступает в роли директивы nvcc, указывает на то, что данная функция doubleMatrix будет обрабатываться в вычислительном устройстве:

mod = SourceModule(""" 
  __global__ void doubleMatrix(float *a)
	   

Давайте рассмотрим тело нашего ядра. Значение параметра idx является индексом матрицы, которая посредством threadIdx.x и threadIdx.y указывает координаты потока:

int idx = threadIdx.x + threadIdx.y*4;
a[idx] *= 2;
	   

Далее mod.get_function("doubleMatrix") возвращает некий идентификатор для значения параметра func:

func = mod.get_function("doubleMatrix ")
	   

Для выполнения своего ядра нам требуется настроить значение контекста исполнения. Это означает настройку соответствующей трёхмерной структуры имеющихся потоков, которые относятся к создаваемому блоку решётки при помощи значения параметра блока внутри самого вызова func:

func(a_gpu, block = (5, 5, 1))
	   

block = (5, 5, 1) сообщает нам что мы вызываем некую функцию ядра с соответствующей лианеризованной входной матрицей a_gpu и единственным блоком с размером 5 (то есть с 5 потоками) в направлении x-, 5 потоками по направлению y- и 1 потоком в направлении z-, что создаёт в сумме 16 потоков. Обратите внимание, что каждый из потоков исполняет один и тот же код ядра (в сумме 25 потоков).

После вычисления в имеющемся устройстве GPU мы пользуемся неким массивом для сохранения полученных результатов:

a_doubled = numpy.empty_like(a)
CUDA.memcpy_dtoh(a_doubled, a_gpu)
	   

Для выполнения нашего примера в приглашении своей Командной строки наберите следующее:

C:\> python heterogenousPycuda.py
		

Получаемый вывод должен выглядеть как- то так:

ORIGINAL MATRIX
[[-0.59975582 1.93627465 0.65337795 0.13205571 -0.46468592]
[ 0.01441949 1.40946579 0.5343408 -0.46614054 -0.31727529]
[-0.06868593 1.21149373 -0.6035406 -1.29117763 0.47762445]
[ 0.36176383 -1.443097 1.21592784 -1.04906416 -1.18935871]
[-0.06960868 -1.44647694 -1.22041082 1.17092752 0.3686313 ]]

DOUBLED MATRIX AFTER PyCUDA EXECUTION
[[-1.19951165 3.8725493 1.3067559 0.26411143 -0.92937183]
[ 0.02883899 2.81893158 1.0686816 -0.93228108 -0.63455057]
[-0.13737187 2.42298746 -1.2070812 -2.58235526 0.95524889]
[ 0.72352767 -2.886194 2.43185568 -2.09812832 -2.37871742]
[-0.13921736 -2.89295388 -2.44082164 2.34185504 0.73726263 ]]
		

Основным ключевым свойством CUDA, которое делает эту модель программирования по большей части отличающейся от прочих моделей программирования (обычно применяемых в ЦПУ), состоит в том, что для достижения эффективности она требует задействовать тысячи потоков. Это делает возможным в обычных структурах GPU, которые применяют потоки с малым весом, а также допускают создание и изменение контекста выполнения очень быстрым и действенным образом.

Обратите внимание, что планирование потоков напрямую связано с имеющейся архитектурой GPU и присущему ей параллелизму. На практике некий блок потоков назначается отдельному SM. Здесь все потоки далее делятся на группы посредством имеющегося обёртывающего планировщика (warp scheduler). Для достижения полного преимущества внутренне присущего параллелизма существующих SM и потоков одна и та же обёртка обязана выполнять одну и ту же инструкцию. Когда такое условие не выполняется, мы говорим о расхождении потоков (threads divergence).

Программы PyCUDA обязаны соблюдать предписанные установленной структурой и внутренней организацией SM правила, которые налагают ограничения на производительность потоков. На практике знание и правильное применение различных видов предоставляемых GPU памяти имеют основополагающее значение для достижения максимальной эффективности. В таких GPU, в которых включено использование CUDA, существует четыре следующих вида памяти:

Таким образом, для лучшей производительности некая программа PyCUDA должна максимально использовать все виды имеющейся памяти. В частности она должна максимально применять общую память, сводя к минимуму доступ к глобальной памяти.

Для этого область решаемой задачи обычно подразделяется таким образом, чтобы один блок потоков мог бы выполнять свою обработку в закрытом подмножестве данных. Тем самым, все работающие в одном блоке потоки будут совместно работать в одной и той же области разделяемой памяти, оптимизируя доступ.

Вот основные шаги, которым следует придерживаться всем потокам:

Для прояснения данного подхода, в своём следующем разделе мы представим некий пример, основывающийся на вычислении произведения двух матриц.

Следующий фрагмент кода показывает вычисление произведения двух матриц, M×N, стандартным методом, который основывается на последовательном подходе. Каждый элемент в получаемой в выводе матрице, P, получается после выборки элементов строки из матрицы M и элементов колонки из матрицы N:

void SequentialMatrixMultiplication(float*M,float *N,float *P, int width){ 
  for (int i=0; i< width; ++i) 
      for(int j=0;j < width; ++j) { 
          float sum = 0; 
          for (int k = 0 ; k < width; ++k) { 
              float a = M[I * width + k]; 
              float b = N[k * width + j]; 
              sum += a * b; 
                     } 
         P[I * width + j] = sum; 
    } 
} 
P[I * width + j] = sum;
 	   

В данном случае, когда каждому потоку придаётся необходимая задача вычисления каждого элемента в результирующей матрице, тогда доступ к памяти будет иметь доминирующее значение в общем времени выполнения такого алгоритма.

Что мы можем сделать, так это положиться на некий блок потоков для вычисления одного вывода частичной матрицы за раз. Таким образом, все потоки, которые имеют доступ к одной и той же памяти блока совместно работают для оптимизации доступа, тем самым минимизируя общее время выполнения:

Давайте рассмотрим рабочий поток программирования PyCUDA. Подготовим необходимые входные матрицы, матрицы вывода и где мы будем хранить полученные результаты:

MATRIX_SIZE = 5
a_cpu = np.random.randn(MATRIX_SIZE, MATRIX_SIZE).astype(np.float32)
b_cpu = np.random.randn(MATRIX_SIZE, MATRIX_SIZE).astype(np.float32)
c_cpu = np.dot(a_cpu, b_cpu)
	   

Затем мы перешлём эти матрицы в вычислительное устройство GPU воспользовавшись функцией PyCUDA gpuarray.to_gpu():

a_gpu = gpuarray.to_gpu(a_cpu)
b_gpu = gpuarray.to_gpu(b_cpu)
c_gpu = gpuarray.empty((MATRIX_SIZE, MATRIX_SIZE), np.float32)
	   

Основной сердцевиной данного алгоритма является приводимая далее функция ядра. Давайте обратим внимание на имеющееся ключевое слово __global__, определяющее что данная функция является функцией ядра, что означает что она будет исполняться вычислительным устройством (GPU), вслед за вызовом из соответствующего кода хоста (ЦПУ):

__global__ void MatrixMulKernel(float *a, float *b, float *c){
    int tx = threadIdx.x;
    int ty = threadIdx.y;
    float Pvalue = 0;
    for (int k = 0; k < %(MATRIX_SIZE)s; ++k) {
        float Aelement = a[ty * %(MATRIX_SIZE)s + k];
        float Belement = b[k * %(MATRIX_SIZE)s + tx];
        Pvalue += Aelement * Belement;}
    c[ty * %(MATRIX_SIZE)s + tx] = Pvalue;
}
	   

threadIdx.x и threadIdy.y это координаты, которые позволяют указывать конкретные потоки в имеющейся решётке двухмерных блоков. Обратите внимание, что такие потоки внутри установленной решётки блоков выполняют один и тот же код ядра, но с разными частями данных. Если мы сравним свою параллельную версию с последовательной, тогда мы немедленно заметим, что наши индексы циклов i и j были заменены на соответствующие индексыthreadIdx.x и threadIdy.y.

Это означает, что в нашей параллельной версии у нас будет иметься лишь одна итерация данного цикла. На практике наше ядро MatrixMulKernel будет выполнено некой решёткой с размерностью потоков 5 х 5.

Это условие отображается на следующей схеме:

Затем мы проверяем полученное произведение просто сравнивая две полученные в результате матрицы:

np.allclose(c_cpu, c_gpu.get())
	   

Получаемый вывод следующий:

C:\> python memManagementPycuda.py

---------------------------------------------------------------------
Matrix A (GPU):
[[ 0.90780383 -0.4782407 0.23222363 -0.63184392 1.05509627]
 [-1.27266967 -1.02834761 -0.15528528 -0.09468858 1.037099 ]
 [-0.18135822 -0.69884419 0.29881889 -1.15969539 1.21021318]
 [ 0.20939326 -0.27155793 -0.57454145 0.1466181 1.84723163]
 [ 1.33780348 -0.42343542 -0.50257754 -0.73388749 -1.883829 ]]
---------------------------------------------------------------------
Matrix B (GPU):
[[ 0.04523897 0.99969769 -1.04473436 1.28909719 1.10332143]
 [-0.08900332 -1.3893919 0.06948703 -0.25977209 -0.49602833]
 [-0.6463753 -1.4424541 -0.81715286 0.67685211 -0.94934392]
 [ 0.4485206 -0.77086055 -0.16582981 0.08478995 1.26223004]
 [-0.79841441 -0.16199949 -0.35969591 -0.46809086 0.20455229]]
---------------------------------------------------------------------
Matrix C (GPU):
[[-1.19226956 1.55315971 -1.44614291 0.90420711 0.43665022]
 [-0.73617989 0.28546685 1.02769876 -1.97204924 -0.65403283]
 [-1.62555301 1.05654192 -0.34626681 -0.51481217 -1.35338223]
 [-1.0040834 1.00310731 -0.4568972 -0.90064859 1.47408712]
 [ 1.59797418 3.52156591 -0.21708387 2.31396151 0.85150564]]
---------------------------------------------------------------------

TRUE
		

Размещённые в совместной памяти данные обладают ограниченной видимостью в однопоточном блоке. Легко обнаружить что представленная модель программирования PyCUDA адаптируется к конкретным классам приложений.

В частности, те свойства, которые должны представлять эти приложения связаны с наличием множества математических операций, причём с высокой степенью параллелизма (то есть одна и та же последовательность операций повторяется на больших объёмах данных).

Те области приложений, которые овладевают этими характеристиками относятся к следующим наукам: криптография, вычислительная химия, а также анализ изображений и сигналов.

Дополнительные примеры использования PyCUDA можно обнаружить по следующей ссылке.

PyOpenCL является братским проектом по отношению к PyCUDA. Это библиотека привязок, которая предоставляет полный доступ к API OpenCL из Python, причём также от Андреаса Клёкнера. Он оснащён множеством тех же самых понятий что и PyCUDA, включая очистку от вышедших из сферы объектов, частичног абстрагирование от структур данных, а также обработку ошибок, причём всё это с минимумом накладных расходов. Этот проект доступен по лицензии MIT; его документация очень хороша и в открытом доступе можно найти обилие руководств и учебных пособий.

Основное средоточие PyOpenCL состоит в предоставлении некого обладающего лёгким весом соединения между Python и OpenCL, но он также содержит поддержку шаблонов и метапрограмм. Основной поток программы PyOpenCL почти в точности та же самая, что и у программ C и C++ для OpenCL. Сама программа хоста подготавливаем необходимые вызовы программ вычислительного устройства, запускает их, а затем дожидается полученных результатов.

Основной ссылкой для установки PyOpenCL является домашняя страница Андреаса Клёкнера.

Если вы применяете Anaconda, то она предлагает такие шаги:

В своём следующем примере мы воспользуемся некой функцией PyOpenCL, которая позволит нам перенумеровать все свойства того GPU, с которым она будет работать.

Необходимый для этого код очень прост и логичен:

Следующая команда применяется для импорта библиотеки pyopencl:

import pyopencl as cl
	   

Это делает для нас доступным метод get_platforms, который возвращает список экземпляров платформы,то есть перечень устройств для данной системы:

for platform in cl.get_platforms():
	   

Затем для каждого обнаруженного устройства отображаются следующие основные свойства:

Для нашего примера вывод таков:

(base) C:\> python deviceInfoPyopencl.py

=============================================================
OpenCL Platforms and Devices
============================================================
Platform - Name: NVIDIA CUDA
Platform - Vendor: NVIDIA Corporation
Platform - Version: OpenCL 1.2 CUDA 10.1.152
Platform - Profile: FULL_PROFILE
    --------------------------------------------------------
    Device - Name: GeForce 840M
    Device - Type: GPU
    Device - Max Clock Speed: 1124 Mhz
    Device - Compute Units: 3
    Device - Local Memory: 48 KB
    Device - Constant Memory: 64 KB
    Device - Global Memory: 2 GB
    Device - Max Buffer/Image Size: 512 MB
    Device - Max Work Group Size: 1024
============================================================
Platform - Name: Intel(R) OpenCL
Platform - Vendor: Intel(R) Corporation
Platform - Version: OpenCL 2.0
Platform - Profile: FULL_PROFILE
    --------------------------------------------------------
    Device - Name: Intel(R) HD Graphics 5500
    Device - Type: GPU
    Device - Max Clock Speed: 950 Mhz
    Device - Compute Units: 24
    Device - Local Memory: 64 KB
    Device - Constant Memory: 64 KB
    Device - Global Memory: 3 GB
    Device - Max Buffer/Image Size: 808 MB
    Device - Max Work Group Size: 256
    --------------------------------------------------------
    Device - Name: Intel(R) Core(TM) i7-5500U CPU @ 2.40GHz
    Device - Type: CPU
    Device - Max Clock Speed: 2400 Mhz
    Device - Compute Units: 4
    Device - Local Memory: 32 KB
    Device - Constant Memory: 128 KB
    Device - Global Memory: 8 GB
    Device - Max Buffer/Image Size: 2026 MB
    Device - Max Work Group Size: 8192
		

OpenCL в настоящее время управляется Khronos Group, некоммерческим консорциумом компаний, которые сотрудничают в определении спецификаций этого (и многих иных) стандартов и параметров совместимости для создания особенных для OpenCL драйверов всех видов платформ.

Такие драйверы также предоставляют функции для вычислительных программ, которые пишутся на языке ядра: они преобразуются в программы некого вида промежуточного языка, который обычно является особым для производителя, а затем исполняются на эталонной архитектуре.

Дополнительные сведения по OpenCL можно найти по следующей ссылке.

Самый первый шаг построения программы для PyOpenCL состоит в написании кода самого приложения хоста. Он выполняется на основном ЦПУ и обладает задачей управления всем возможным исполнением своего ядра в имеющейся карте GPU (то есть в вычислительном устройстве).

Некое ядро (kernel) является базовым элементом исполняемого кода, аналогичного функции C. Он может быть параллельным для данных или параллельным для задач. Однако замковым камнем PyOpenCL выступает сама эксплуатация параллелизма.

Основополагающим понятием является некая программа, которая является коллекцией ядер и прочих функций, аналогичных динамическим библиотекам. Поэтому мы обладаем возможностью группирования инструкций в неком ядре и группировании различных ядер в какую- то программу.

Программы могут вызываться из приложений. Мы имеем очереди исполнения, которые указывают установленный порядок, в котором исполняются ядра. Однако, в некоторых случаях их можно запускать не следуя первоначальному порядку.

Наконец, мы можем перечислить все основополагающие элементы для разработки некого приложения при помощи PyOpenCL:

Ниже приводится схема, отображающая как такая структура данных может работать в неком приложении хоста:

И снова мы наблюдаем, что наша программа способна содержать дополнительные функции для исполнения в вычислительном устройстве и что каждое ядро инкапсулирует лишь единственную функцию из имеющейся программы.

В своей следующей программе мы покажем все основные шаги построения некого приложения с помощью PyOpenCL: основная задача для выполнения состоит в суммировании двух векторов. Чтобы обладать читаемым выводом, мы рассмотрим два вектора, которые обладают 100 элементами: каждый i-й элемент получаемого вектора будет эквивалентен сумме i-го элемента vector_a с i-м элементом vector_b:

В своих приводимых ниже строках, после надлежащего импорта, мы определяем свои входные векторы:

vector_dimension = 100
vector_a = np.random.randint(vector_dimension, size= vector_dimension)
vector_b = np.random.randint(vector_dimension, size= vector_dimension)
	   

Каждый вектор содержит 100 целых элементов, которые выбираются случайным образом посредством соответствующей функции numpy:

np.random.randint(max integer , size of the vector)
	   

Далее мы выбираем необходимую платформу для получения своих вычислений, воспользовавшись методом get_platform():

platform = cl.get_platforms()[1]
	   

После этого выбираем соответствующее устройство. В нашем случае, platform.get_devices()[0] соответствует графической карте Intel(R) HD Graphics 5500:

device = platform.get_devices()[0]
	   

На своём следующем шаге определяются значения контекста и очереди; PyOpenCL предоставляет соответствующие методы контекста (выбранного устройства) и очереди (выбранного контекста):

context = cl.Context([device])
queue = cl.CommandQueue(context)
	   

Для осуществления вычислений в выбранном устройстве, наш входной вектор копируется в память необходимого устройства:

mf = cl.mem_flags 
a_g = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR,\
hostbuf=vector_a) 
b_g = cl.Buffer(context, mf.READ_ONLY | mf.COPY_HOST_PTR,\
 hostbuf=vector_b)
	   

Далее мы подготавливаем необходимый буфер для получаемого в результате вектора:

res_g = cl.Buffer(context, mf.WRITE_ONLY, vector_a.nbytes)
	   

Вот как задаётся код необходимого ядра:

program = cl.Program(context, """ 
__kernel void vectorSum(__global const int *a_g, __global const int *b_g, __global int *res_g) { 
  int gid = get_global_id(0); 
  res_g[gid] = a_g[gid] + b_g[gid];} 
""").build()
	   

Названием нашего ядра является vectorSum, а имеющийся список параметров определяет все типы данных входных аргументов и тип данных на выходе (оба являются векторами целых значений). Внутри самого тела ядра задаётся сумма двух векторов следующей последовательностью шагов:

В OpenCL (а следовательно и в PyOpenCL), значения буферов присоединяются к контексту (подробнее...), который перемещается в устройство, когда такой буфер применяется в этом устройстве.

Наконец, мы выполняем в своём устройстве vectorSum:

program.vectorSum(queue, vector_a.shape, None, a_g, b_g, res_g)
	   

Для проверки полученного результата мы применяем оператор assert. Он Сверяет полученный результат и выставляет некую ошибку когда результат ложен:

assert(la.norm(res_np - (vector_a + vector_b))) < 1e-5
	   

Получаемый вывод должен выглядеть как- то так:

(base) C:\> python vectorSumPyopencl.py 

PyOPENCL SUM OF TWO VECTORS
Platform Selected = Intel(R) OpenCL
Device Selected = Intel(R) HD Graphics 5500
VECTOR LENGTH = 100
INPUT VECTOR A

[45 46 0 97 96 98 83 7 51 21 72 70 59 65 79 92 98 24 56 6 70 64 59 0
 96 78 15 21 4 89 14 66 53 20 34 64 48 20 8 53 82 66 19 53 11 17 39 11
 89 97 51 53 7 4 92 82 90 78 31 18 72 52 44 17 98 3 36 69 25 87 86 68
 85 16 58 4 57 64 97 11 81 36 37 21 51 22 17 6 66 12 80 50 77 94 6 70
 21 86 80 69]

INPUT VECTOR B
[25 8 76 57 86 96 58 89 26 31 28 92 67 47 72 64 13 93 96 91 91 36 1 75
  2 40 60 49 24 40 23 35 80 60 61 27 82 38 66 81 95 79 96 23 73 19 5 43
  2 47 17 88 46 76 64 82 31 73 43 17 35 28 48 89 8 61 23 17 56 7 84 36
 95 60 34 9 4 5 74 59 6 89 84 98 25 50 38 2 3 43 64 96 47 79 12 82
 72 0 78 5]

OUTPUT VECTOR RESULT A + B
[70 54 76 154 182 194 141 96 77 52 100 162 126 112 151 156 111 117 152 
 97 161 100 60 75 98 118 75 70 28 129 37 101 133 80 95 91 130 58 74 134 
 177 145 115 76 84 36 44 54 91 144 68 141 53 80 156 164 121 151 74 35 
 107 80 92 106 106 64 59 86 81 94 170 104 80 76 92 13 61 69 171 70 87 
 125 121 119 76 72 55 8 69 55 144 146 124 173 18 152 93 86 158 74]
		

В данном разделе мы рассмотрели модель выполнения PyOpenCL, которая как и PyCUDA, привлекает процесор хоста, управляющий одним или более разнородных устройств. В частности, каждая команда PyOpenCL отправляется в надлежащее устройство из своего хоста в виде исходного кода, который определяется посредством необходимой функции ядра.

Такой исходный код далее загружается в некий объект программы для эталонной архитектуры, эта программа компилируется для такой эталонной архитектуры, и создаётся надлежащий объект ядра, соотносимый с данной программой.

Объект ядра может выполняться в произвольном числе рабочих групп, создавая некую n- мерную вычислительную матрицу, что позволяет ему действенно подразделять общую рабочую нагрузку для задачи на n- измерений (1, 2 или 3) в каждой из рабочих групп. В свою очередь, они составляются в некое число исполнительных элементов, которые работают параллельно.

Балансировка общей рабочей нагрузки каждой рабочей группы, основывающаяся на имеющейся возможности параллельных вычислений некого устройства, является одним из критически важных параметров для достижения достойной производительности приложения.

Ненадлежащая балансировка имеющейся рабочей нагрузки, совместно с конкретными особенностями каждого устройства (такими как задержки н обмен, пропускная способность и полоса пропускания) могут приводить к существенным потерям производительности или к компромиссам в присутствии переносимости вашего кода при выполнении без учёта сведений динамичного получения системы вычислений в плане вычислительных возможностей устройства.

Однако аккуратное применение таких технологий позволяет нам достигать высоких уровней производительности в сочетании с получаемыми результатами вычислений для различных вычислительных устройств.

С дополнительными сведениями по программированию PyOpenCL можно ознакомиться по следующей ссылке.

Функциональность поэлементных выражений позволяет нам вычислять ядра сложных выражений (которые составляются из большого числа операндов) за один вычислительный проход.

Для поэлементной обработки в PyOpenCL реализуется метод ElementwiseKernel (context, argument, operation, name, optional_parameters) .

Его основные параметры таковы:

Здесь мы снова рассмотрим задачу сложения двух векторов.

В самых первых строках своего сценария мы импортируем все необходимые нам модули.

Для инициализации своего контекста мы применяем метод cl.create_some_context(). Он запрашивает у пользователя какой именно контекст требуется применять для данного вычисления:

Choose platform:
[0] <pyopencl.Platform 'NVIDIA CUDA' at 0x1c0a25aecf0>
[1] <pyopencl.Platform 'Intel(R) OpenCL' at 0x1c0a2608400> 
		

Вслед за этим нам требуется установить экземпляр своей очереди, которая будет получать ElementwiseKernel:

queue = cl.CommandQueue(context)
 	   

Создаются экземпляры входных и выходного векторов. Наши входные векторы, vector_a и vector_b, являются векторами целочисленных значений, получаемых при помощи функции NumPy random.randint. Эти векторы, за этим, копируются в вычислительное усройство при помощи соответствующего оператора PyOpenCL:

cl.array_to_device(queue,array)
 	   

В ElementwiseKernel создаётся некий объект:

elementwiseSum = cl.elementwise.ElementwiseKernel(context,\
               "int *a, int *b, int *c", "c[i] = a[i] + b[i]", "sum")
 	   

Наконец, мы вызываем свою функцию elementwiseSum с заданными ранее значениями аргументов:

elementwiseSum(vector_a, vector_b, result_vector)
 	   

Данный пример завершается выводом на печать значений входных векторов и получаемого результата. Наш вывод выглядит как- то так:

(base) C:\>python elementwisePyopencl.py

Choose platform:
[0] <pyopencl.Platform 'NVIDIA CUDA' at 0x1c0a25aecf0>
[1] <pyopencl.Platform 'Intel(R) OpenCL' at 0x1c0a2608400>
Choice [0]:1

Choose device(s):
[0] <pyopencl.Device 'Intel(R) HD Graphics 5500' on 'Intel(R) OpenCL' at 0x1c0a1640db0>
[1] <pyopencl.Device 'Intel(R) Core(TM) i7-5500U CPU @ 2.40GHz' on 'Intel(R) OpenCL' at 0x1c0a15e53f0>
Choice, comma-separated [0]:0
PyOpenCL ELEMENTWISE SUM OF TWO VECTORS
VECTOR LENGTH = 100
INPUT VECTOR A
[24 64 73 37 40 4 41 85 19 90 32 51 6 89 98 56 97 53 34 91 82 89 97 2
 54 65 90 90 91 75 30 8 62 94 63 69 31 99 8 18 28 7 81 72 14 53 91 80
 76 39 8 47 25 45 26 56 23 47 41 18 89 17 82 84 10 75 56 89 71 56 66 61
 58 54 27 88 16 20 9 61 68 63 74 84 18 82 67 30 15 25 25 3 93 36 24 27
 70 5 78 15]

INPUT VECTOR B
[49 18 69 43 51 72 37 50 79 34 97 49 51 29 89 81 33 7 47 93 70 52 63 90
 99 95 58 33 41 70 84 87 20 83 74 43 78 34 94 47 89 4 30 36 34 56 32 31
 56 22 50 52 68 98 52 80 14 98 43 60 20 49 15 38 74 89 99 29 96 65 89 41
 72 53 89 31 34 64 0 47 87 70 98 86 41 25 34 10 44 36 54 52 54 86 33 38
 25 49 75 53]

OUTPUT VECTOR RESULT A + B
[73 82 142 80 91 76 78 135 98 124 129 100 57 118 187 137 130 60 81 184 
 152 141 160 92 153 160 148 123 132 145 114 95 82 177 137 112 109 133 
 102 65 117 11 111 108 48 109 123 111 132 61 58 99 93 143 78 136 37 145 
 84 78 109 66 97 122 84 164 155 118 167 121 155 102 130 107 116 119 50 
 84 9 108 155 133 172 170 59 107 101 40 59 61 79 55 147 122 57 65 
 95 54 153 68]
		

PyCUDA также обладает поэлементной функциональностью:

cl.array_to_device(queue,array)
 	   

Эта функциональность обладает во многом совпадающими аргументами со встроенной в PyOpenCL, за исключением параметра контекста. Тот же самый пример что и в данном разделе, который реализован для PyCUDA имеет такой листинг:

import pycuda.autoinit 
import numpy 
from pycuda.elementwise import ElementwiseKernel 
import numpy.linalg as la 
 
vector_dimension=100 
input_vector_a = np.random.randint(100,size= vector_dimension) 
input_vector_b = np.random.randint(100,size= vector_dimension) 
output_vector_c = gpuarray.empty_like(input_vector_a) 
 
elementwiseSum = ElementwiseKernel(" int *a, int * b, int *c",\ 
                             "c[i] = a[i] + b[i]"," elementwiseSum ") 
elementwiseSum(input_vector_a, input_vector_b,output_vector_c) 
 
print ("PyCUDA ELEMENTWISE SUM OF TWO VECTORS") 
print ("VECTOR LENGTH = %s" %vector_dimension) 
print ("INPUT VECTOR A") 
print (vector_a) 
print ("INPUT VECTOR B") 
print (vector_b) 
print ("OUTPUT VECTOR RESULT A + B ") 
print (result_vector)
 	   

По данной ссылке вы обнаружите занимательные примеры приложений PyOpenCL.

В данном разделе мы выполняем сопоставительное тестирование производительности между ЦПУ и GPU с применением библиотеки PyOpenCL.

Действительно, прежде чем изучать получаемую производительность подлежащего реализации алгоритма, также важно понимать те вычислительные преимущества, которые предлагает имеющаяся у вас вычислительная платформа.

Конкретные вычислительные характеристики вычислительной системы влияют на время вычисления, а следовательно они являют собой сторону первостепенной важности.

В своём следующем примере мы выполним некую проверку для наблюдения производительности в такой системе:

В нашем последующем тесте будет оцениваться и сравниваться время вычисления некой математической операции, а именно сложения двух векторов из элементов с плавающей точкой. Для выполнения такого сопоставления, одна и та же операция будет выполнена в двух раздельных функциях.

Наша первая функция выполняется только в имеющемся ЦПУ, в то время как вторая функция написана с применением PyOpenCL для использования установленной карты GPU. Данный тест выполняется для вектора с размером в 10 000 элементов.

Вот наш код:

Как пояснялось ранее, наш тест состоит в выполнении нашей задачи вычислений, причём обе в ЦПУ посредством функции test_cpu_vector_sum, а затем через установленное GPU при помощи функции test_gpu_vector_sum.

Обе функции выдают отчёт о времени выполнения.

Что касается функции проверки на ЦПУ, test_cpu_vector_sum, она состоит из двух вычислительных циклов по 10000 элементам векторов:

cpu_start_time = time() 
               for i in range(10000): 
                         for j in range(10000): 
                             c_cpu[i] = a[i] + b[i] 
               cpu_end_time = time()
	   

Значение общего времени ЦПУ составляет разницу между следующим:

CPU Time = cpu_end_time - cpu_start_time
	   

Что касается функции test_gpu_vector_sum, просматривая ядро выполнения вы можете видеть следующее:

__kernel void sum(__global const float *a, 
                      __global const float *b, 
                      __global float *c){ 
        int i=get_global_id(0); 
        int j; 
        for(j=0;j< 10000;j++){ 
            c[i]=a[i]+b[i];}
	   

Значение суммы двух векторов выполняется через единственный цикл вычислений.

Полученный результат, как и можно было ожидать, состоит в значительном снижении во времени вычисления для функции test_gpu_vector_sum:

(base) C:\> python testApplicationPyopencl.py 
 
============================================================
OpenCL Platforms and Devices
============================================================
Platform - Name: NVIDIA CUDA
Platform - Vendor: NVIDIA Corporation
Platform - Version: OpenCL 1.2 CUDA 10.1.152
Platform - Profile: FULL_PROFILE
    --------------------------------------------------------
    Device - Name: GeForce 840M
    Device - Type: GPU
    Device - Max Clock Speed: 1124 Mhz
    Device - Compute Units: 3
    Device - Local Memory: 48 KB
    Device - Constant Memory: 64 KB
    Device - Global Memory: 2 GB
    Device - Max Buffer/Image Size: 512 MB
    Device - Max Work Group Size: 1024
============================================================
Platform - Name: Intel(R) OpenCL
Platform - Vendor: Intel(R) Corporation
Platform - Version: OpenCL 2.0
Platform - Profile: FULL_PROFILE
    --------------------------------------------------------
    Device - Name: Intel(R) HD Graphics 5500
    Device - Type: GPU
    Device - Max Clock Speed: 950 Mhz
    Device - Compute Units: 24
    Device - Local Memory: 64 KB
    Device - Constant Memory: 64 KB
    Device - Global Memory: 3 GB
    Device - Max Buffer/Image Size: 808 MB
    Device - Max Work Group Size: 256
    --------------------------------------------------------
    Device - Name: Intel(R) Core(TM) i7-5500U CPU @ 2.40GHz
    Device - Type: CPU
    Device - Max Clock Speed: 2400 Mhz
    Device - Compute Units: 4
    Device - Local Memory: 32 KB
    Device - Constant Memory: 128 KB
    Device - Global Memory: 8 GB
    Device - Max Buffer/Image Size: 2026 MB
    Device - Max Work Group Size: 8192


CPU Time: 39.505873918533325 s
GPU Kernel evaluation Time: 0.013606592 s
GPU Time: 0.019981861114501953 s
		

Даже несмотря на то, что наш тест не блещет вычислительной выразительностью, он предоставляет полезное указание на значительный потенциал карты GPU.

OpenCL является стандартным крос- платформенным API для разработки приложений, которые эксплуатируют параллельное вычисление в неоднородных системах. Примечательна аналогия с CUDA, включая всё, начиная с имеющейся иерархии памяти, вплоть до непосредственного соответствия между потоками и элементами исполнения.

Даже на самом уровне программирования имеется множество аналогичных сторон и расширений с одной и той же функциональностью.

Однако OpenCL имеет намного более сложную модель управления устройством по причине способности поддержки широкого разнообразия аппаратных средств. С другой стороны, OpenCL разработан для того чтобы получать переносимость между продуктами различных производителей.

Благодаря большей зрелости и узкой специализации аппаратных средств, CUDA предлагает более простое управление устройством и API более высокого уровня, которые делают его более предпочтительным, но только когда вы имеете дело с конкретными архитектурами (то есть графическими картами nVidia).

В своих последующих разделах мы поясняем за и против библиотек CUDA и OpenCL, а также PyCUDA и PyOpenCL.

За OpenCL и PyOpenCL

Аргументы за таковы:

Против OpenCL и PyOpenCL

Аргументы против таковы:

За CUDA и PyCUDA

Аргументы за такие:

Против CUDA и PyCUDA

Аргументы против такие:

Анлреас Клёкнер сделал ряд лекций по программированию GPU пр помощи PyCuda и PyOpenCL, доступные по ссылкам в ​www.​bu.​edu и www.​youtube.​com.

Numba является компилятором Python, который предоставляет основанный на CUDA API. Он разработан в первую очередь для задания численных вычислений, точно также как и библиотека NumPy. В частности, библиотека numba управляет типы массивов данных, предоставляемых NumPy и обрабатывает их.

Действительно, такая эксплуатация параллелизма данных, которая является присущей численным вычислениям с привлечением массивов, является естественным выбором для ускорителей GPU.

Компилятор работает с особыми типами сигнатур (или декораторов) для функций Python и делает возможной компиляцию времени исполнения (такой тип компиляции также имеет название Как раз вовремя, JiT - Just In Time).

Наиболее важными декораторами являются следующие:

Numba (выпуск 0.45) совместим с Python 2.7 и 3.5 или более поздними версиями, а также с версиями NumPy с 1.7 до 1.16.

Для установки numba рекомендуется, как и для pyopencl, применять инфраструктуру Anaconda, а потому в приглашении Anaconda просто наберите следующее:

(base) C:\> conda install numba
		

Кроме того, для применения всего потенциала numba следует установить библиотеку cudatoolkit:

(base) C:\> conda install cudatoolkit
		

После этого можно проверить будут ли определяться как положено библиотека CUDA и GPU.

Из приглашения Anaconda откройте интерпретатор Python:

(base) C:\> python
Python 3.7.3 (default, Apr 24 2019, 15:29:51) [MSC v.1915 64 bit (AMD64)] :: Anaconda, Inc. on win32
Type "help", "copyright", "credits" or "license" for more information.
>> 
		

Самая первая проверка влечёт за собой проверку того установлена ли как положено библиотека CUDA (cudatoolkit):

>>> import numba.cuda.api
>>> import numba.cuda.cudadrv.libs
>>> numba.cuda.cudadrv.libs.test()
		

Последующий вывод показывает такое качество нашей установки, при котором все проверки возвращают положительный результат:

Finding cublas from Conda environment
 located at C:\Users\Giancarlo\Anaconda3\Library\bin\cublas64_10.dll
 trying to open library... ok
Finding cusparse from Conda environment
 located at C:\Users\Giancarlo\Anaconda3\Library\bin\cusparse64_10.dll
 trying to open library... ok
Finding cufft from Conda environment
 located at C:\Users\Giancarlo\Anaconda3\Library\bin\cufft64_10.dll
 trying to open library... ok
Finding curand from Conda environment
 located at C:\Users\Giancarlo\Anaconda3\Library\bin\curand64_10.dll
 trying to open library... ok
Finding nvvm from Conda environment
 located at C:\Users\Giancarlo\Anaconda3\Library\bin\nvvm64_33_0.dll
 trying to open library... ok
Finding libdevice from Conda environment
 searching for compute_20... ok
 searching for compute_30... ok
 searching for compute_35... ok
 searching for compute_50... ok
True
		

В своей второй проверке мы удостоверяем присутствие графической карты:

>>> numba.cuda.api.detect()
		

Полученный вывод показывает обнаружена ли графическая карта и поддерживается ли она:

Found 1 CUDA devices
id 0 b'GeForce 840M' [SUPPORTED]
                      compute capability: 5.0
                           pci device id: 0
                              pci bus id: 8
Summary:
        1/1 devices are supported
True
		

В данном примере мы предоставляем демонстрацию компилятора Numba с применением аннотации @guvectorize.

Наша задача состоит в умножении матриц:

Наш декоратор @guvectorize обрабатывает аргументы массивов, получая четыре аргумента для определения значения сигнатуры gufunc:

Затем определяется операция матричного умножения, где A и B выступают в роли входных матриц, а C это выходная матрица: A(m,n)* B(n,p) = C(m,p), где m, n и p являются размерностями матриц.

Произведение матриц выполняется посредством трёх циклов for совместно со значениями индексов матриц:

for i in range(m): 
            for j in range(p): 
                C[i, j] = 0 
                for k in range(n): 
                      C[i, j] += A[i, k] * B[k, j]
	   

Для построения входных матриц с размерностью 10 × 10 применяется функция NumPy randint:

dim = 10
A = np.random.randint(dim,size=(dim, dim))
B = np.random.randint(dim,size=(dim, dim))
	   

Наконец, для этих матриц в качестве аргументов вызывается наша функция matmul и выводится на печать получаемая в результате матрица C:

C = matmul(A, B)
print("RESULT MATRIX C = A*B")
print(":\n%s" % C)
	   

Для выполнения этого примера наберите следующее:

(base) C:\> python matMulNumba.py
		

Приводятся результаты заданных двух матриц и полученную в результате их умножения матрицу:

INPUT MATRIX A
:
[[8 7 1 3 1 0 4 9 2 2]
 [3 6 2 7 7 9 8 4 4 9]
 [8 9 9 9 1 1 1 1 8 0]
 [0 5 0 7 1 3 2 0 7 3]
 [4 2 6 4 1 2 9 1 0 5]
 [3 0 6 5 1 0 4 3 7 4]
 [0 9 7 2 1 4 3 3 7 3]
 [1 7 2 7 1 8 0 3 4 1]
 [5 1 5 0 7 7 2 3 0 9]
 [4 6 3 6 0 3 3 4 1 2]]
INPUT MATRIX B
:
[[2 1 4 6 6 4 9 9 5 2]
 [8 6 7 6 5 9 2 1 0 9]
 [4 1 2 4 8 2 9 5 1 4]
 [9 9 1 5 0 5 1 1 7 1]
 [8 7 8 3 9 1 4 3 1 5]
 [7 2 5 8 3 5 8 5 6 2]
 [5 3 1 4 3 7 2 9 9 5]
 [8 7 9 3 4 1 7 8 0 4]
 [3 0 4 2 3 8 8 8 6 2]
 [8 6 7 1 8 3 0 8 8 9]]
RESULT MATRIX C = A*B
:
[[225 172 201 161 170 172 189 230 127 169]
 [400 277 289 251 278 276 240 324 295 273]
 [257 171 177 217 208 254 265 224 176 174]
 [187 130 116 117 94 175 105 128 152 114]
 [199 133 117 143 168 156 143 214 188 157]
 [180 118 124 113 152 149 175 213 167 122]
 [238 142 186 165 188 215 202 200 139 192]
 [237 158 162 176 122 185 169 140 137 130]
 [249 160 220 159 249 125 201 241 169 191]
 [209 152 142 154 131 160 147 161 132 137]]
		

Написание алгоритма для операции снижения ранга при помощи PyCUDA может быть достаточно сложным. Для этой цели Numba предоставляет декоратор @reduce для преобразования простых двоичных операций в понижающие ядра (reduction kernels).

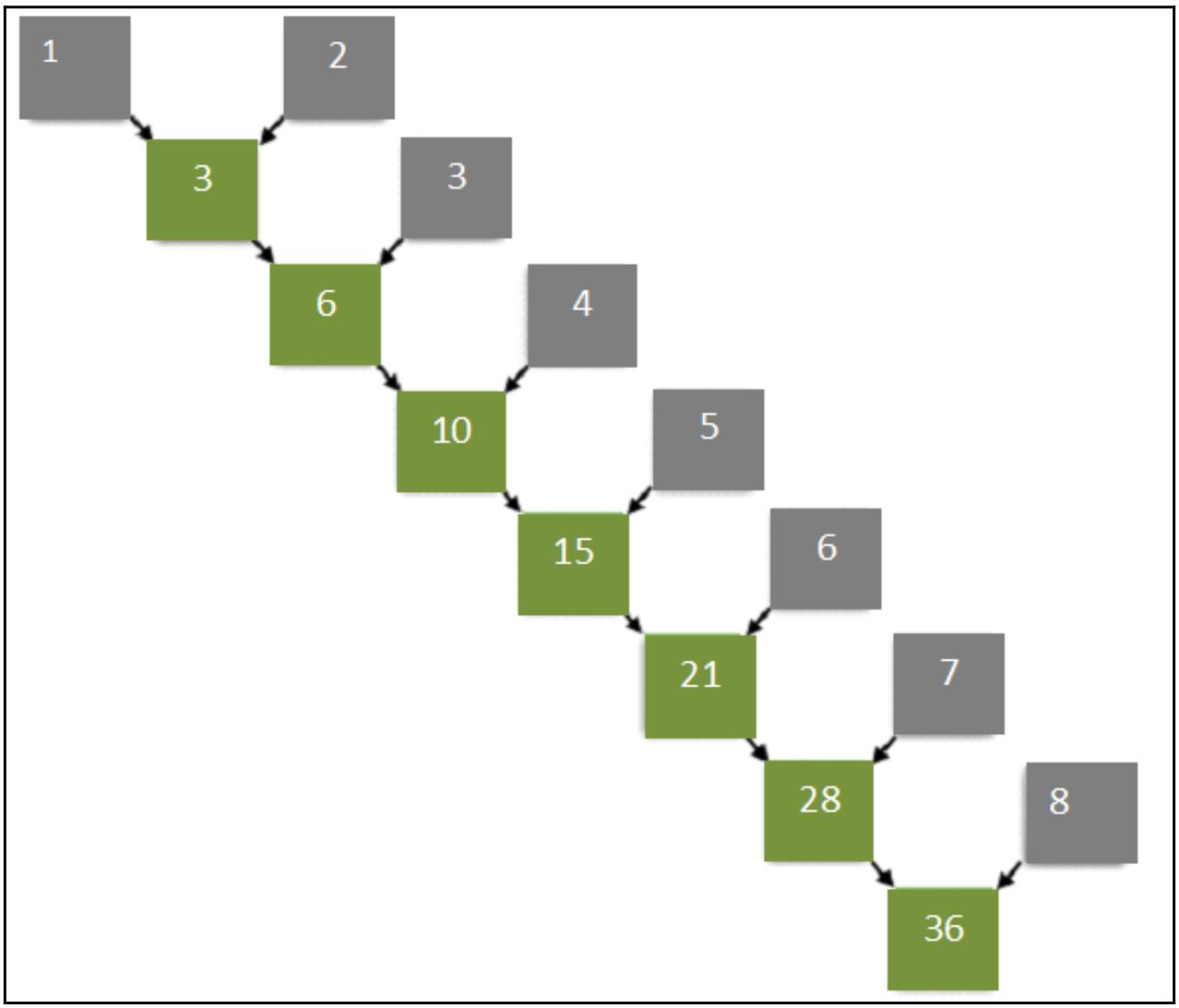
Операции снижения ранга сводят набор значений к отдельному значению. Типичным примером понижающей операции является вычисление суммы всех элементов массива. в качестве примера рассмотрим следующий массив элементов: 1, 2, 3, 4, 5, 6, 7, 8.

Последовательный алгоритм работает так, как это показано на следующей схеме, то есть добавляя элементы данного массива один за другим:

Параллельный же алгоритм работает по следующей схеме:

Становится ясно, что последний имеет определённое преимущество в сокращении времени исполнения.

С помощью Numba и установленного декоратора @reduce мы способны написать некий алгоритм в несколько строк кода для значения параллельного суммирования некого массива целых в диапазоне от 1 до 10 000:

import numpy 
from numba import cuda 
 
@cuda.reduce 
def sum_reduce(a, b): 
    return a + b 
 
A = (numpy.arange(10000, dtype=numpy.int64)) + 1
print(A) 
got = sum_reduce(A)
print(got)
	   

Наш предыдущий пример может быть выполнен после набора такой команды:

(base) C:\> python reduceNumba.py
		

Будет представлен такой результат:

vector to reduce = [ 1 2 3 ... 9998 9999 10000]
result = 50005000
	   

В этом репозитории вы можете обнаружить множество примеров Numba. Интересное введение в программирование Numba и CUDA можно найти по следующей ссылке.