Глава 3. Начальные сведения из математики
Содержание
Чтобы разобраться с тем как функционирует файловая система, прежде всего, необходимо понимать как в вычислительной системе представляется информация. Компьютеры и, естественно, все электронные цифровые устройства по своей природе являются двоичными, что означает, что они обладают способностью обрабатывать только 0 и 1. Надлежащая интерпретация длинных последовательностей 0 и 1 влечёт за собой все те сведения, которые пребывают в вычислительных системах: числам, тексту, изображениям, потокам аудио, электронным таблицам, базам данных и так далее.
Для проведения цифрового криминалистического анализа и, что более важно, для понимания результатов цифрового криминалистического анализа, сначала необходимо разбираться в лежащей в основе системе хранения, которая применяется для всех типов данных.
Данная глава изучает как в вычислительных системах представляются числа, тексты и время. Она изучает системы счисления, показывая как десятичная соотносится с двоичной и шестнадцатеричной, а также как выполнять преобразования между этими системами счисления. Приводится введение в различные применяемые для представления текста системы кодирования, в особенности в те, которые наиболее часто встречаются, такие как ASCII, ISO-8859, UTF-8 и UTF-16. В расследовании время играет жизненно важное значение и, как правило, вычислительные системы предоставляют большой объём сведений о времени. А раз так, данная глава обсуждает как представляется время в различных операционных и файловых системах. Наконец, данная глава покажет как в действительности информация хранится на жёстком диске либо в обратном, либо в прямом (big-endian или little-endian) форматах. При прямом порядке (little-endian) последовательность байт изменяется, что означает, что перед началом интерпретации данные прямой последовательности должны преобразовываться в формат обратной последовательности. Окончательная цель этой главы состоит в том, чтобы снабдит читателя навыками интерпретации вручную сырых данных, с которыми он сталкивается в ходе расследования.
Чтобы поддерживать действенное общение о представлении информации в вычислительных системах, для начала требуется разобраться с определённой терминологией. Когда речь заходит о ёмкости/ размере хранения, наиболее фундаментальной единицей выступает бит, одна единственная двоичная цифра. Следовательно, бит обладает значением 0 или 1.
Компьютеры собирают биты в более крупные и более сложные структуры. Таблица 3.1 суммирует такие структурные единицы. Сколько значений способна хранить каждая из таких структур? Метод расчёта числа возможных представляемых определённым числом бит значений довольно прост. Всего навсего возведите 2 в значение числа бит. Это суммирует Таблица 3.2.
| Число бит | Термин |
|---|---|
|
Бит |
|
Полубайт (Nibble) |
|
Байт (Byte) |
|
Слово (Word) |
|
Целое двойной длины или Длинное слово(Long или Double Word) |
|
Плавающее двойной длины или 64- битное целое (Very Long) |
| Число бит | Количество значений |
|---|---|
|
21 = 2d |
|
24 = 16d |
|
28 = 256d |
|
216 = 65 536d |
|
232 = 4 294 967 296d |
|
264 = 18 446 744 073 709 551 616d |
Эти знания служат подсказкой о том, как именно информация хранится в компьютерах, а также почему существуют определённые ограничения! Рассмотрим адреса протокола Интернета версии 4 (IPv4). Знания о сетях сообщают нам, что эти адреса состоят из четырёх разделённых точками десятичных чисел от 0 до 255. Например, 192.168.1.12 — допустимый IP-адрес. Но многие спрашивают, почему такое странное максимальное число, почему не 999?
Основная причина данного ограничения кроется в Таблице 3.2. Когда возможные значения для каждого числа в пределах от 0 до 255, тогда в общей сложности имеется 256 значений. Единственный байт (восемь бит) также допускает 256 значений. IP адреса ограничены числами от 0 до 255, поскольку для представления этих чисел они пользуются четырьмя индивидуальными байтами. Вы также могли слышать, что всего имеется только около 4 миллионов IPv4 адресов. Придерживаясь той теории, что IP адрес состоит из четырёх байт, мы получаем, что IP адрес целиком это структура из 32 бит. Следовательно, её ограничение составляет только около четырёх миллионов адресов. Таблица 3.2 показывает, что 32 бита способны представлять 4 294 967 296d возможных значений, что в точности совпадает с количеством возможных IP адресов!
Но как насчёт больших значений? Одной из самых больших проблем в компьютерной криминалистике является огромный требующий обработки объем информации. Мы не говорим, что диск обладает ёмкостью 1 099 511 627 776d байт: вместо этого мы говорим 1 терабайт (хотя это и неверно, как будет показано через одно мгновение!).
Прежде чем приступать к рассмотрению более крупных групп байтов, необходимо определить, будут ли они измеряться в десятичной или в двоичной системе счисления. Традиционно, более крупные единицы хранения могут измеряться как 1000x байтов или как 1024x байтов. Первый случай — это десятичная (по основанию 10) система счисления, также называемая системой СИ (Международная система единиц), тогда как второй случай — это двоичная система счисления. Когда люди ссылаются на большие наборы байтов, зачастую возникает путаница относительно того, что именно имеется в виду. Таблица 3.3 суммирует более крупные наборы байтов и названия/обозначения, которые будут применяться в данной книге.
| Десятичные | Двоичные | ||||
|---|---|---|---|---|---|
| Символ | Префикс | Значение | Символ | Префикс | Значение |
|
Kilo |
103 = 10001 |
|
Kibi |
210 = 10241 |
|
Mega |
106 = 10002 |
|
Mibi |
220 = 10242 |
|
Giga |
109 = 10003 |
|
Gibi |
230 = 10243 |
|
Tera |
1012 = 10004 |
|
Tebi |
240 = 10244 |
|
Peta |
1015 = 10005 |
|
Pebi |
250 = 10245 |
|
Exa |
1018 = 10006 |
|
Exbi |
260 = 10246 |
|
Zetta |
1021 = 10007 |
|
Zebi |
270 = 10247 |
|
Yotta |
1024 = 10008 |
|
Yobi |
280 = 10248 |
Таблица 3.3 показывает, что килобайт означает 1000 байт, в то время как кибибайт представляет 1024 байта. Эти значения в повседневной речи часто неверно применяются в качестве как синонимов, а порой и поставщиками дисков!
Рассматриваемые до сих пор структуры основаны на кратных байту, но что насчёт структур меньшего размера? Байты можно разбивать на меньшие структуры, в которых группы отдельных битов представляют определённые фрагменты информации. Они носят название полей бит (bit fields). Для демонстрации полей бит мы приводим классический пример - значение даты и времени FAT.
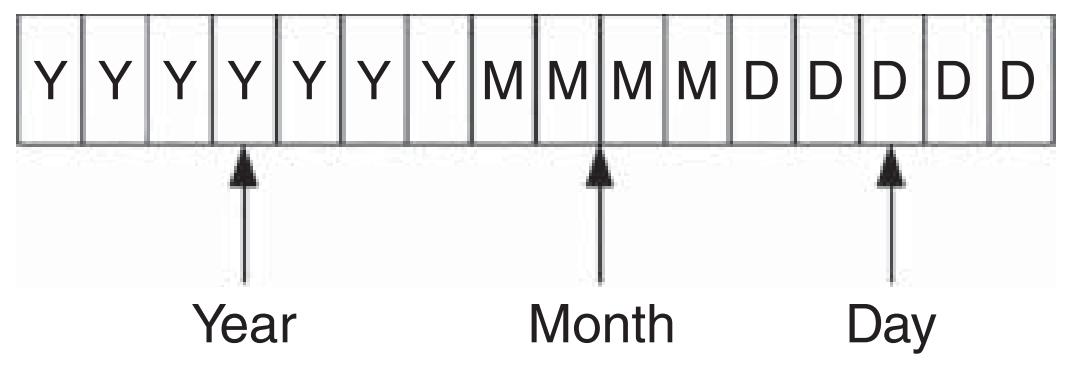
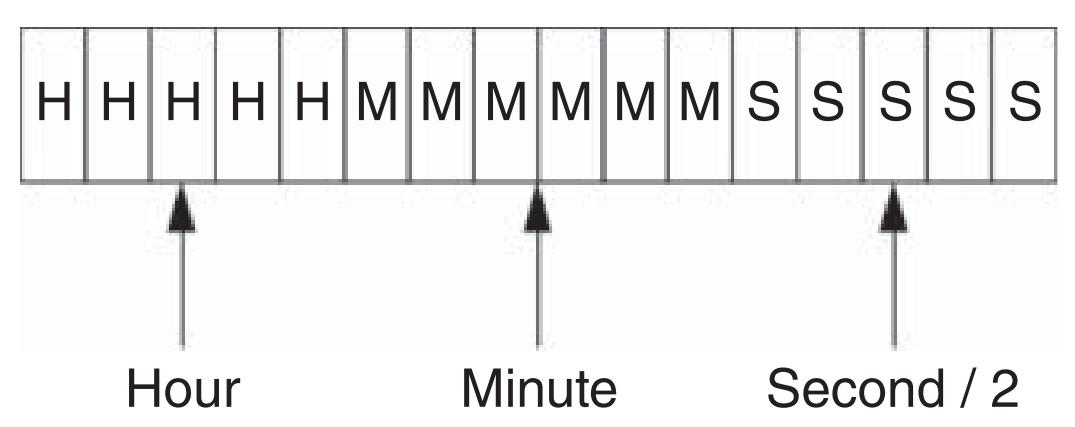
Дата и время FAT встречаются в файловых системах FAT для хранения метаданных. Файловая система записывает даты Изменения, Доступа и Создания (Modified, Accessed и Created), наряду временами Изменения и Создания (Modified и Created). Все эти значения хранятся как значения Даты/ Времени FAT, которое является двумя байтами, составленными из полей бит. Рисунки 3.1 и 3.2 отражают структуры Даты и Времени FAT, соответственно.
В значении даты FAT пять наименее значимых бит представляют значение дня. Пять бит допускают 25 (32d) возможных значений, достаточных для хранения значений от 1 до 31, чтобы представлять все допустимые дни месяца. Следующие четыре бита представляют значение месяца, четыре бита допускают 24 (16d) значений. Это оставляет семь бит для представления значения года. Семь бит допускают 27 (128d) возможных значений, или года 0 - 127 нашей эры. Очевидно, что компьютеры были не столь широко распространены в 127 году после рождества Христова, а потому для верного представления года дата FAT начинается с 1980 года. Следовательно, когда мы в этом поле обнаруживаем 41d, это представляет нам 2021 год.
Время FAT хранит сведения аналогичным образом. Пять наиболее значимых бит представляют значение часа. Пять бит предоставляют 32d значений, достаточно для отображения чисел 0-23d. Последующие шесть бит представляют значения минут, шесть бит достаточно для 64d. Это оставляет пять бит для представления секунд. Однако, пять бит допускают лишь 32d возможных значения (0-31d), что означает невозможность представления всех значений. Вместо этого время FAT представляет значение секунд, делённое на два, а не реально число секунд. Это подразумевает, что файловая система FAT различает лишь действия которые происходят в интервале двух секунд.
Поля бит (более ранняя форма технологии хранения) в современных системах применяются редко. Они были обусловлены стоимостью пространства хранения на ранней стадии. Значение имел каждый байт, а потому пространство никогда не тратилось зазря. В последние годы стоимость хранения снизилась настолько сильно, что это ограничение более не значимо. Таким образом, маловероятно применение полей бит современными системами, хотя мы порой всё ещё сталкиваемся с ними.
Одной из самых первых вещей, необходимых для представления (и интерпретации) являются численные данные. Для хранения численных данных компьютеры применяют двоичную систему счисления. Данный раздел изучает численные системы счисления в целом, прежде чем перейти к рассмотрению наиболее часто встречающихся численных систем при вычислениях, а именно, десятичной (той, которую воспринимают люди), двоичной (поскольку компьютеры пользуются только нулями и единицами) и шестнадцатеричной (так как шестнадцатеричное является самым простым методом представления двоичных данных). Основным отличием между численными системами счисления выступает их основание, то количество уникальных цифр, которое содержит эта система счисления. Двоичным основанием выступает 2 (цифрами являются 0 и 1), десятичное основание это 10 (цифры 0-9) и шестнадцатеричное основание равно 16 (цифры 0-9 совместно с A-F).
После того как системы счисления были описаны, этот раздел продолжит показывать как выполнять преобразование между системами счисления. Базовые системы счисления допускают для представления лишь натуральные числа (то есть, неотрицательные целые: 0, 1, 2, 3, ...). Компьютерам требуется представлять нечто большее чем это; таким образом, окончательные темы этого раздела изучат как компьютеры представляют также отрицательные числа и числа с плавающей запятой. Тем не менее, прежде чем продолжать, необходимо ввести соглашения об обозначениях, которые будут применяться на протяжении всего остатка данной книги.
Когда люди видят такое число как 100, основное их предположение состоит в том, что это именно десятичное число со значением ста. Для аналитика криптографии это число может быть представлено в любой из систем счисления (скорее всего, в двоичной, десятичной и шестнадцатеричной). Таким образом, для верной интерпретации данного значения применяется соглашение об обозначениях, которое наряду с числом указывает систему счисления. Достичь этого можно множеством способов. Например, для записи 100 в виде десятичного числа можно использовать любое из следующих обозначений:
-
0d100
-
100d
-
10010
Во всяком конкретном случае становится ясно, что число 100d пребывает в десятичной системе счисления, что делает возможным для аналитиков верно интерпретировать его значение. Как правило, для представления основы счисления применяется буква, d для десятичной (decimal), b для двоичной (binary), x (или h) для шестнадцатеричной (hex) и o для восьмеричной (octal). Также может применяться реальная основа системы счисления, как это видно в последнем примере, 10010. Это в особенности полезно при использовании некой не стандартной системы счисления. Например, некое значение по основанию системы счисления 5 может быть записано как 1235. На протяжении этой книги приведённые выше соглашения будут применяться для представления всех чисел!
Десятичная система счисления фактически стандарт в повседневной жизни. Большая часть нашего мира пользуется десятичными в качестве стандарта. Исторически существовали некоторые важные исключения из этого. Например, Шумерская и Вавилонская цивилизации пользовались системой счисления по основанию 60, в то время как многие Южноамериканские культуры (к примеру, Ацтеки и Майя) применяли систему счисления по основанию 20. И в самом деле, множество представителей народов в Северной Америке применяют в наши дни систему счисления по основанию 20 (цифры Кактовик).
Десятичная система счисления является примером системы счисления с привязкой к местоположению. В системе счисления с привязкой к местоположению значение цифры представляет собой сочетание самой цифры и того места, которое она занимает в общем числе. Рассмотрим десятичное число 333d. Это число состоит из нескольких цифр, каждая из которых имеет разное значение в зависимости от её расположения. Если вы помните, что изучали в начальной школе, то, скорее всего, изучали, что 333d - это три сотни, три десятка и три единицы (также называемые единицами измерения). Это основа системы счисления с привязкой по местоположению. Все современные системы счисления (независимо от их основы) работают подобным образом.
Если быть более точным, при использовании системы счисления с привязкой к местоположению, всякому местоположению присваивается некий показатель степени. Начиная с наименее значимого местоположения (то есть с самой правой позиции) с показателем ноли и с возрастанием на единицу для каждого следующего местоположения по мере продвижения влево. Для получения значения цифры в определённом месте, величина основания возводится в степень значения экспоненты, а затем умножается на эту цифру. Ниже это показано для числа 333d. Поскольку это десятичное число, основание равно 10.
333d
Digits 3 | 3 | 3
Exponents 2 | 1 | 0
Values 3 * 102 | 3 * 101 | 3 * 100
= 3 * 100 | 3 * 10 | 3 * 1
= 300d | 30d | 3d
Total 300 + 30 + 3 = 333d
Приведённый выше результат кажется тривиальным, он просто показывает, что 333d = 333d. Однако он гораздо более фундаментален, чем может показаться на первый взгляд. Все современные системы счисления пользуются системой местоположений, что означает, что приведённая выше система остаётся верной в каждом конкретном случае. Как только известно основание числа, соответствующее десятичное значение может быть запросто вычислено с помощью приведённой выше системы счисления.
Двоичная система счисления пользуется основанием 2, что подразумевает, что существует лишь две допустимых цифры (обычно именуемых битом), которыми выступают 0 и 1. Двоичное исчисление жизненно важно для нашего понимания об информации, поскольку в электронном устройстве хранения именно так представляются сведения. И снова двоичное представление пользуется системой значения по местоположению, при котором основанием выступает 2. Рассмотрим число 1011b. Для преобразования его в десятичное представление применяется система значений по местоположению. Это показывается ниже.
1011d
Digits 1 | 0 | 1 | 1
Exponents 3 | 2 | 1 | 0
Values 1 * 23 | 0 * 22 | 1 * 21 | 1 * 20
= 3 * 8 | 0 * 4 | 1 * 2 | 1* 1
= 8d | 0d | 2d | 1d
Total 8 + 0 + 2 +1 = 11d
Следовательно, значению двоичного 1011b эквивалентно 11d.
Шестнадцатеричные это обычно встречающаяся при цифровой криминалистике система счисления по основанию 16. Шестнадцатеричные применяют цифры 0 - 9 наряду с буквами A - F, где A равно 10, B равно 11 и C равно 12 и так далее. И вновь шестнадцатеричные пользуются системой значения по местоположению, что подразумевает, что преобразование этих значений в десятичное тривиально. Рассмотрим число 1AEx. Преобразование этого числа в десятичное представление даёт:
1AEx
Digits 1 | A | E
Exponents 2 | 1 | 0
Values 1 * 162 | A * 161 | E * 160
= 1 * 256 | 10 * 16 | 14 * 1
= 256d | 160d | 14d
Total 256 + 160 + 14 = 430d
Шестнадцатеричные зачастую применяются в цифровой криминалистике для более простого представления сырых данных. Хотя, как уже неоднократно подчёркивалось, что сырые данные в электронной системе хранения запоминаются только в двоичном формате, это не обязательно самый лучший способ просмотра сырых данных. Основной причиной этого является сложность. Рассмотрим данные, показанные на Рисунках 3.3 и 3.4. Рисунок 3.3 показывает двоичное представление сырых данных, в то время как Рисунок 3.4 отображает те же самые данные в шестнадцатеричной форме. Хотя вы, возможно, ещё и не до конца разбираетесь в двоичной или шестнадцатеричной системе счисления, я уверен, вы согласитесь, что шестнадцатеричные данные выглядят для понимания немного проще (хотя бы из-за меньшего объёма данных).
Основная причина, по которой так часто применяется шестнадцатеричная система счисления, состоит в соотношении между двоичными и шестнадцатеричными. Двоичная система счисления - это система счисления по основанию 2, в то время как шестнадцатеричная система счисления - это система счисления по основанию 16 или 24. Это соотношение означает, что четыре бита могут быть представлены одной шестнадцатеричной цифрой, а байт может быть представлен двумя шестнадцатеричными цифрами. Для преобразования между двумя системами счисления необходимо всего лишь найти значения в Таблице 3.4.
| Binary | Hex | Binary | Hex | Binary | Hex | Binary | Hex |
|---|---|---|---|---|---|---|---|
|
0 |
|
4 |
|
8 |
|
C |
|
1 |
|
5 |
|
9 |
|
D |
|
2 |
|
6 |
|
A |
|
E |
|
3 |
|
7 |
|
B |
|
F |
Рассмотрим шестнадцатеричное число 1AEx. Его можно преобразовать в двоичное при помощи Таблицы 3.4. Каждая индивидуальная шестнадцатеричная цифра преобразуется в своё соответствующее двоичное значение чтобы получить: 0b0001 1010 1110. Идущие впереди нули можно удалить, что приводит в результате к: 0b1 1010 1110.
Обратный процесс достаточно прост. Двоичные цифры можно сочетать по четыре и замещать соответствующими шестнадцатеричными значениями. Наш процесс группирования начинается с правой стороны преобразуемого двоичного числа. Рассмотрим двоичное число 0b1111000110. Его группирование справа в результате приводит к трём индивидуальным числам: 11, 1100 and 0110. Преобразуем их согласно Таблице 3.4 и получим в результате шестнадцатеричное значение 0x3C6.
При помощи системы значения по местоположению число по любому основанию может быть преобразовано в десятичное представление. Самый последний вопрос, который надлежит задать, это как десятичное число преобразовать в число по другому основанию? Самый простой способ для этого заключается в повторяемом делении. При повторяемом делении значение преобразуемого числа циклически делится на значение желаемого основания. Остаток от этого деления записывается и затем в результате получается искомое значение. Рассмотрим число 100d. Каково его значение в двоичном представлении? Применение повторяемого деления приводит в результате к:
100∕2 == 50 R.0 ↑
50∕2 == 25 R.0 ↑
25∕2 == 12 R.1 ↑
12∕2 == 6 R.0 ↑
6∕2 == 3 R.0 ↑
3∕2 == 1 R.1 ↑
1∕2 == 0 R.1 ↑
Процесс деления в цикле останавливается по достижению 0 в результате. Затем для выдачи ответа полученные остатки (Remainders) считываются снизу вверх, в данном случае: 1100100b. Получаемый результат любого цифрового преобразования всегда можно проверить обратным процессом. Преобразование 1100100b в десятичное представление должно иметь результатом 100d.
Тот же самый процесс используется для преобразования десятичного в шестнадцатеричное. Преобразуемое значение циклически делится на величину основания, к которому мы желаем выполнить преобразование (16d) и записываются остатки. Вот результат данного процесса:
100∕16 == 6 R.4 ↑
6∕16 == 0 R.6 ↑
Считываем остатки снизу вверх и получаем 0x64. И снова этот результат может быть подтверждён обратным процессом!
Для преобразования чисел можно пользоваться целым рядом способов терминалом Bash. Одним из простейших средств преобразования любого числа в десятичное представление состоит в арифметическом операторе подстановки $((…)). Листинг 3.1 отображает два метода преобразования числа 1AC16 в десятичный вид.
Листинг 3.1. Применение арифметической подстановки для преобразования в Bash чисел в десятичные
$ echo $((16#1AC))
428
$ echo $((0x1AC))
428
Текущее основание определяется как 16# (или 0x), за которым непосредственно следует подлежащее преобразованию число. Результатом является представление десятичного значения для этого шестнадцатеричного числа. То же самое можно выполнить для любого иного значения основания для преобразования в десятичное представление. К примеру, Листинг 3.2 показывает преобразование 10101100b в десятичное представление.
Листинг 3.2. Преобразование двоичных чисел в десятичные при помощи арифметической подстановки
$ echo $((2#10101100))
172
Для преобразования десятичного в иную систему счисления требуется внешняя программа с названием bc. Применение bc отражено в Листинге 3.3.
Листинг 3.3. Применение bc для преобразования в иные системы счисления
$ echo "obase=16; ibase=10; 428" | bc
1AC
В Листинге 3.3 заранее определяются основания счисления на входе ibase и на выходе obase. Наконец, предоставляется значение числа по основанию на входе. Всё это конвейером отправляется в bc, которая выполняет необходимое преобразование. Обратите внимание на то, что значением основания для входа и выхода по умолчанию выступает 10, а потому команда echo "obase=16; 428" | bc производит то же самое действие, что и в Листинге 3.3. Тем не менее, для преобразования любых пар систем счисления можно пользоваться форматом в общем виде (то есть определяя основу и на входе, и на выходе). Листинг 3.4 показывает преобразование двоичного в шестнадцатеричное, а Листинг 3.5 отображает преобразование шестнадцатеричного в представление по основанию 5.
Листинг 3.4. Применение bc для преобразования двоичного в шестнадцатеричное
$ echo "obase=16; ibase=2; 101010" | bc
2A
Листинг 3.5. Применение bc для преобразования шестнадцатеричного в представление по основанию 5
$ echo "obase=5; ibase=16; C" | bc
22
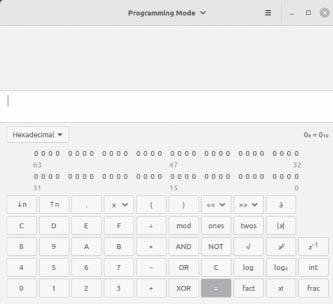
Естественно, если требуется ещё более простой способ преобразования между стандартными системами счисления, можно применять встроенный калькулятор с графическим интерфейсом, как это показано на Рисунке 3.5. Встроенный калькулятор в Linux Mint (показан на Рисунке 3.5) позволяет выбрать режим программирования. В этом режиме пользователь может выбрать основание для ввода (на Рисунке 3.5 выбрана десятичная система). Любое введённое значение будет отображаться в трёх иных системах счисления (калькулятор поддерживает четыре системы счисления: 2 (двоичная), 8 (восьмеричная), 10 (десятичная) и 16 (шестнадцатеричная)).
До данного момента мы изучали только натуральные (то есть неотрицательные целые) числа и их представление. А что относительно отрицательных целых чисел? В этом разделе рассматривается дополнительный код числа, один из наиболее распространённых методов представления отрицательных целых чисел.
Таблица 3.2 показывает показывает, что число из 8 бит может представлять 256d (28) отличающихся значений без знака (положительных). В 8- битном дополнительном коде числа наиболее значимый (самый левый) бит представляет знак. Когда наиболее значимый бит равен нулю, число положительное, но если бит знака равен единице, тогда число отрицательное. В случае положительного числа значение просто вычисляется так же, как и для числа без знака; однако в случае отрицательного числа необходимо выполнить дополнительные шаги. Учитывая, что число 0xA7 является 8-битным дополнительным кодом числа, необходимо вычислить его значение. Для этого сначала преобразуем число в двоичную форму, что даёт 0b1010 0111.
Отсюда наиболее значимый бит равен единице, что означает, что это отрицательное число. Затем получается инверсия всех бит и к результату добавляется единица. Такое значение носит название дополнения. Далее это дополнение преобразуется в десятичное представление для получения абсолютного значения числа. Это процесс показан ниже:
Number: 0b10100111
Inverse: 0b01011000
Complement: 0b01011001
Absolute Value: 89d
Decimal: -89d
При использовании дополняющего кода необходимо знать количество бит для представления этого числа, чтобы определять какой именно бит является наиболее значимым и представляет знак числа.
Существуют альтернативные способы представления в вычислительных системах отрицательных чисел, такие как дополнение до единицы, знак с величиной, а также двоичное смещение . Тем не менее, хотя это и не самая простая форма, дополнительный код является наиболее часто встречающемся. Это обусловлено той простотой, с которой математические операции могут выполняться при использовании чисел в дополнительном коде на уровне ЦПУ.
Вещественные числа это другой вид данных, который порой требуется при вычислениях. Наиболее распространённой формой хранения являются числа с плавающей запятой. В них десятичная точка {Прим. пер.: запятая в русскоязычной литературе, но мы будем придерживаться терминологии десятичной точки} может плавать; иными словами, её позиция не установлена раз и навсегда, а вместо этого может перемещаться чтобы допускать большие числа с потерей точности или представлять меньшие числа с гораздо большей точностью. Чтобы продемонстрировать это понятие, давайте вкратце рассмотрим десятичную систему счисления.
Когда для представления числа допускаются 10 цифр, необходимо делать выбор. Если десятичная точка помещается после восьми цифр в числах от 0 до 99 999 999, может быть представлен весьма значительный диапазон, однако точность числа ограничена двумя десятичными знаками (10-2). Когда, с другой стороны, наша десятичная точка помещается после второй цифры, может быть представлен намного меньший диапазон, все число от 0 до 99, однако для большей точности после точки доступно больше места, восемь знаков (10-8). Именно такой компромисс присутствует при использовании числе с плавающей точкой: либо число обладает очень большим диапазоном при ограниченной точности, или большая точность с меньшим диапазоном.
Прежде чем представлять двоичные числа с плавающей точкой, необходимо познакомиться с двоичными числами с фиксированной точкой. Предположим, что вещественное число представляется при помощи единственного байта, в котором четыре наиболее значимых бита представляют целую часть числа, а четыре наименее значимых бита представляют дробную часть числа. Рассмотрим байт, содержащий 01101010b, на самом деле это 0110.1010b, поскольку это число с фиксированной точкой. Для вычисления его значения можно воспользоваться Таблицей 3.5. Обратите внимание на то, насколько этот процесс для числа с фиксированной точкой схож с тем, который мы применяли для целого. Всё ещё применяется система местоположений, однако используются иные значения местоположений (некоторые степени теперь отрицательные!).
| 23 | 22 | 23 | 20 | 2-1 | 2-2 | 2-3 | 2-4 |
|---|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
Как и в случае со стандартным двоичным целым, десятичное значение получается путём умножения двух последних строк в Таблице 3.5 и сложения результата, чтобы получить:
(1 * 4) + (1 * 2) + (1 * 1∕2) + (1 * 1∕8)
=
4 + 2 + 0.5 + 0.125
=
6.625d
Следовательно двоичное число с фиксированной точкой 0110.1010b обладает десятичным значением 6.625d.
Как мы уже упоминали ранее, числа с фиксированной точкой обладают ограничениями. Например, в показанной выше схеме с единственным байтом можно представлять только 24 целых чисел (0-15d), причём совместно с 24 дробных частей. Если же мы пожелаем представлять такие числа, как 24d или 1.234d, это невозможно сделать при таком подходе. При схеме чисел с плавающей точкой можно представить оба эти значения.
В математике числа часто представляются в научной нотации, например 3.1 * 10d-3. Оно имеет значение 0.0031d. При данном научном выражении такое число делится на две части, первая, 3.1, носит название мантиссы (m), в то время как второе, 10-3, это его основание (10d), возведённое в показатель степени (e, экспонента). Обычно все десятичные числа могут представляться в показанном в Выражении 3.1 виде:
m * 10e (3.1)
Такой же в точности подход применяется и для двоичных чисел. Вещественное двоичное число может быть представлено при помощи представленного в Выражении 3.2 виде:
m * 2e (3.2)
при котором для вычислительных целей изменяется лишь значение основания исчисления. Таким образом, числа с плавающей точкой составляются сочетанием мантиссы и экспоненты (степени показателя). Рассмотрим пример, в котором значение 1.1101b * 23 должно храниться в формате с плавающей точкой из 12 бит, при котором один бит резервируется под знак, семь бит резервируются под мантиссу, а четыре применяются для степени показателя (экспоненты). Сохраняется собственно дробная часть мантиссы сама по себе, в то время как значение экспоненты хранится как второе сопутствующее число. Всё это представляется как 0110 1000 0011.
Представленное выше двоичное число с плавающей точкой может быть преобразовано в десятичное с применением системы местоположений со значением, как это показано в Таблице 3.6. Самый значимый бит равен нулю, что означает, что это число положительное.
| Знак | Мантисса | Экспонента | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Значение |
|
|
|
|
|
|
|
|
|
|
|
|
Цифра |
0(+) |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
Согласно Таблице 3.6 дробная часть мантиссы определяется равной 1.1101b (с учётом пропущенной части целого числа), что имеет десятичное значение 1 + 0.5 + 0.25 + 0.0625 = 1.8125d. Десятичное значение показателя степени (экспоненты) равно 3d. Таким образом, десятичным значением числа с плавающей точкой задаётся так:
1.8125 * 23 = 14.5d
Приведённая выше схема чисел с плавающей точкой не встречается на практике. Её размер (12 бит) был выбран произвольным образом. Наиболее распространённый из применяемых в вычислительных системах формат для хранения чисел с десятичной точкой основывается на стандарте IEEE 754 (его последняя версия была выпущена в 2019 году, IEEE 754-2019), который {в частности} определяет два стандарта для чисел с плавающей точкой, формат из 32-бит с одинарной точностью и формат из 64-бит с двойной точностью. Каждый из этих форматов делится на три различные части, значение знака, величина мантиссы и степень показателя. И 32-, и 64- битный форматы применяют наиболее значимый бит для представления знака. 32- битный формат использует следующие 8 бит для представления значения смещённого показателя степени, а остающиеся 23 бита для дробной части величины мантиссы. Формат 64-бит для значения смещённого показателя степени применяет 11 бит и 52 бита для дробной части величины мантиссы. Вместо значения экспоненты хранится значение смещённого показателя степени. Это подразумевает, что для получения реального значения показателя степени (экспоненты) из величины смещённого показателя степени надлежит вычесть 127d. Это делает возможным отрицательных чисел даже для значений показателя степени без знака. Что отличается от более простой схемы, которую мы представляли, при которой применялось значение со знаком. Аналогично, значение мантиссы обычно исключает первую 1, которая подразумевается по умолчанию. Иными словами, сохраняется именно дробная составляющая значения мантиссы. Это демонстрируется ниже. Оба формата для хранения данных используют в точности один и тот же метод.
Для упрощения в этом разделе применяется 32-битный формат.
Вот пример 32-битного числа с плавающей запятой:
0100 0001 0101 1010 0000 0000 0000 0000b
В этом примере различающиеся поля выделены подчёркиванием. Отсюда ясно, что бит знака равен нулю, то есть это положительное число. Значение показателя степени представлено как 10000010b, что равно 130d; однако это смещённое значение, следовательно надлежит вычесть 127d, что в результате приводит к величине степени показателя 3d. Значение мантиссы определяется как .101101b; тем не менее, опущена первая 1, что означает, что величина мантиссы равна 1.101101b. Полученное значение мантиссы затем сдвигается на основании величины показателя степени (3d), что приводит к окончательному результату 1101.101b, которое далее можно преобразовать в 13.625d.
Оба формата IEEE 754 работают аналогичным образом. Тем не менее, существуют ограничения при представлении в вычислительных системах вещественных чисел. Точно могут быть представлены в двоичном виде лишь "круглые" двоичные числа (то есть те, что составляются суммой 1/2, 1/4, 1/8, ... и так далее, в общем виде 1/2x). К примеру, рассмотрим число 0.2d, его невозможно представить в точном виде в формате IEEE 754. Его ближайшими представлениями (для 32-битного формата) являются 0.19999998d и 0.200000002d. Тем самым, хотя компьютеры считаются прекрасными инструментами для выполнения математических задач, они страдают от определённых ограничений. Эти ограничения часто основаны на том, как представлена лежащая в основе информация.
{Прим. пер.: В последние годы в интересах вычислений для целей Искусственного Интеллекта большую популярность приобретают иные аппаратно реализуемые в ядрах GPU форматы представления чисел с плавающей точкой, как правило, с увеличением числа бит в поле экспоненты за счёт уменьшения числа бит в поле мантиссы, см., например, Bfloat16 или FP32, FP16, BF16 и FP8 — разбираемся в основных типах чисел с плавающей запятой.}
При расследованиях зачастую представляет интерес основная текстовая информация. Для обеспечения верной интерпретации текстовых данных исследователю может оказаться важным её представление. Текст представляется при помощи кодировок символов. При вычислении этих кодировок каждому символу обычно присваивается некий номер. Для представления соответствующего символа затем применяется это число. Самые ранние примеры кодирования символов существовали до появления цифровых вычислительных устройств. Одним из наиболее известных из них является азбука Морзе, в которой для представления символов применяются комбинации коротких и длинных сигналов. Эти кодировки до компьютеров часто не делали различия между прописными и строчными буквами, предоставляя только одну кодировку для каждой буквы. Компьютерные схемы кодирования содержат гораздо больше символов, чем такие ранние кодировки. В данном разделе рассматриваются некоторые из наиболее часто встречающихся кодировок, включая ASCII, ISO-8859 и Unicode.
American Standard Code for Information Interchange (ASCII) изначально был разработан в 1960е. ASCII это схема кодирования с семью битами, что допускает возможность представления максимально 128 (27) символов. Схема ASCII представляет английские буквенные символы, числа и символы пунктуации. В ASCII присутствует итого 95 выводимых на печать символов (52 из которых это буквы в верхнем и нижнем регистрах, что требует дополнительного кодирования). Остающиеся 33 символа носят название управляющих символов. Это не выводимые на печать символы, имеющих происхождение из древних машин телетайпов. Значение многих из этих символов ныне устарело и лишь небольшое их число используется постоянно, например, возврат каретки (carriage return), перевод строки (line feed) и табуляция (tab).
Каждому символу назначен уникальный код. Скажем, буква "b" это 0b1100010 = 0d98 = 0x62. Вся таблица ASCII показана полностью в Таблице 3.7.
| 0_ | 1_ | 2_ | 3_ | 4_ | 5_ | 6_ | 7_ | |
|---|---|---|---|---|---|---|---|---|
|
NUL |
DLE |
sp. |
0 |
@ |
P |
‘ |
p |
|
SOH |
DC1 |
! |
1 |
A |
Q |
a |
q |
|
STX |
DC2 |
" |
2 |
B |
R |
b |
r |
|
ETX |
D3 |
# |
3 |
C |
S |
c |
s |
|
EOT |
D4 |
$ |
4 |
D |
T |
d |
t |
|
ENQ |
NAK |
% |
5 |
E |
U |
e |
u |
|
ACK |
SYN |
& |
6 |
F |
V |
f |
v |
|
BEL |
ETB |
' |
7 |
G |
W |
g |
w |
|
BS |
CAN |
( |
8 |
H |
X |
h |
x |
|
HT |
EM |
) |
9 |
I |
Y |
i |
y |
|
LF |
SUB |
* |
: |
J |
Z |
j |
z |
|
VT |
ESC |
+ |
; |
K |
[ |
k |
{ |
|
FF |
FS |
, |
< |
L |
\ |
l |
| |
|
CR |
GS |
- |
= |
M |
] |
m |
} |
|
SO |
RS |
. |
> |
N |
^ |
n |
~ |
|
SI |
US |
/ |
? |
O |
_ |
o |
DEL |
Чтобы воспользоваться показанной в Таблице 3.7 ASCII таблицей просто следует взглянуть на перекрестие шестнадцатеричного значения в этой таблице. Рассмотрим значение ASCII 0x5D. Отыщем ячейку на пересечении начинающегося с 5_ столбца с заканчивающейся на _D строкой. Значение в этой ячейке это необходимый символ, в данном случае 0x5D "]".
Листинг 3.6 показывает пример кодированного ASCII текста. Его можно обработать при помощи Таблицы 3.7 и получить текст "ASCII Encoding.\n" Данный текст содержит два специальных символа. Первым является 0x20, представляющий пробел, а второй 0x0A представляет конец строки. (Для тех, кто ещё помнит старые пишущие машинки, по достижению конца строки, барабан возвращался в самое левое положение. Это вызывало два действия: возврат каретки в самое левое положение страницы, а бумага передвигалась на одну линию. При использовании машин телетайпа оба этих символа содержались в ASCII как 0x0D - carriage return - и 0x0A -line feed. В электронном тексте теперь могут быть представлены как оба эти символа - или один из них.)
Листинг 3.6. Пример кодированного в ASCII текста. При его декодировании читаем: "ASCII Encoding.\n"
4153 4349 4920 456e 636f 6469 6e67 2e0a
Каждый байт Листинга 3.6 считывается индивидуально и декодируется (то есть 0x41 это "A", 0x53 это "S" и т.д.). Обратите внимание на заключительный 0x0A, просмотр в Таблице 3.7 приводит к управляющему символу LF. Это символ перехода на новую строку Line Feed). Отметим, что системы Linux по умолчанию для представления новой строки пользуются только 0xOA. Системы на основе Windows/ DOS для представления новой строки обычно применяют два байта, возврат каретки и новая строка (Carriage Return и Line Feed), 0x0D0A.
ASCII ограничена лишь английским языком. В действительности, кое- кто утверждают, что ASCII применяется только в странах, где английский является основным языком, а валютой - доллар! Анализ Таблицы 3.7 показывает, что в ASCII присутствует только один символ валюты - доллар ($). А символы фунта стерлингов (£) или евро (€) отсутствуют, что означает, что ASCII не может применяться в англоязычных странах, использующих такие валюты.
Далее рассмотрим не англоязычные языки. Например, в Ирландии фраза "tá Linux go hiontach" означает, что Linux велик, однако, эту фразу нет возможности представить в ASCII (символ á отсутствует). Более того, ирландский язык содержит символы é, ó, í и ú, помимо соответствующих символов в верхнем регистре, Á, É, Ó, Í и Ú и, естественно, это не единственный дополнительный язык. Необходимо рассматривать все языки.
Следовательно, ASCII не может применяться для Западно- европейских языков. И в самом деле, ситуация становится ещё хуже при дальнейшем движении на Восток, поскольку мы сталкиваемся с различными алфавитами, такими как Кириллица, Греческий, Арабский.
Одним из решений является применение восьми бит для предоставления большего числа символов (если быть точным, ещё 128), чем то, что предоставляет ASCII. Изначально это было именно тем, что именовалось Расширенным ASCII, где первые 128 кодовых позиций идентичны имевшимся в ASCII, а дополнительные 128 можно применять для прочих символов. Было разработано большое число различных расширенных кодировок ASCII для различных стран, задач и т.п. Наконец, International Standards Organisation определила свой собственный стандарт расширения ASCII, в результате приведший к ISO 8859.
Существует ряд вариантов ISO 8859. Самый первый носил название ISO 8859-1 и он содержал необходимые для языков Западной Европы символы. Также он носит название ISO Latin 1. В итоге существует 15 вариантов ISO 8859, от ISO 8859-1 до ISO 8859-16 (ISO 8859-12 был отброшен на этапе разработки и никогда не был выпущен, однако обозначение ISO 8859-12 никогда больше не применялось). Таблица 3.8 подводит итог вариантов ISO 8859. Обратите внимание на то, что для всех вариантов ISO 8859 самые первые 128 символов идентичны имеющимся в базовом ACSII.
| Номер | Название | Описание |
|---|---|---|
|
Latin-1 Western Europe |
Западноевропейские языки, включая Английский, Ирландский, Норвежский, Немецкий, Итальянский, Португальский и Испанский |
|
Latin-2 Central Europe |
Центрально- и Восточно- Европейские языки, пользующиеся латиницей, то есть, Боснийский, Польский, Хорватский, Чешский и Словацкий |
|
Latin-3 South Europe |
Турецкий, Мальтийский и Эсперанто (в целом, заменён 8859-5) |
|
Latin-4 North Europe |
Эстонский, Латвийский, Литовский, Гренландский и Саамский |
|
Latin/ Кириллица |
Языки с алфавитом кириллицы, то есть, Белорусский, Болгарский и Русский {Прим. пер.: практически не применялся для русского, где вместо этого применялись кодировки Win-1251 (или CP1251, базовая в семействах Windows), CP866 (наиболее популярная кодировка на начальных этапах, по причине нетронутости символов псевдографики, в этой кодировке записываются имена файлов в FAT и короткие имена в VFAT), KOI8-R (определена в качестве стандартной для различных ГОСТ, частично для образования подобного текста, получаемого транслитерацией)} |
|
Latin/ Арабский |
Арабские символы |
|
Latin/ Греческий |
Современный греческий алфавит |
|
Latin/ Еврейский |
Современный еврейский алфавит |
|
Latin-5 Turkish |
То же самое, что и Latin-1, но с некоторыми редко используемыми символами, замещёнными на Турецкие |
|
Latin-6 Nordic |
Latin-4 с изменённым порядком для Североевропейских языков. Балтийские языки продолжают применять Latin-4 |
|
Latin-Thai |
Символы Тайского алфавита |
|
Latin/ Devanagari |
Работа прервана |
|
Latin-7 Basic Rim |
Дополнительные символы для Балтийских языков, которые отсутствуют в Latin 4/6 |
|
Latin-8 Celtic |
Гальский и Бретонский языки |
|
Latin-9 |
Предоставляет полную поддержку для Французского, Финского и Эстонского |
|
Latin-10 Юго-восточная Европа |
Полная поддержка для юго-восточных латиниц |
Большое число вариантов ISO 8859 подразумевает, что необходима гарантия верного декодирования перед тем как предпринимать попытку декодирования любого текста. Рассмотрим Ирландское сообщение, "tá Linux go hiontach" , в особенности, остановимся на самом первом слове "tá". Невозможно представить это слово в ASCII, поскольку там отсутствует символ á. Следовательно, необходимо применять один из вариантов ISO 8859 (например, ISO 8859-1). Кодом для в á ISO 8859-1 выступает 0xE1. Таблица 3.9 суммирует значения 0xE1. для всех схем кодирования ISO 8859.
ISO-8859-1 |
|
ISO-8859-9 |
|
ISO-8859-2 |
|
ISO-8859-10 |
|
ISO-8859-3 |
|
ISO-8859-11 |
|
ISO-8859-4 |
|
ISO-8859-13 |
|
ISO-8859-5 |
|
ISO-8859-14 |
|
ISO-8859-6 |
|
ISO-8859-15 |
|
ISO-8859-7 |
|
ISO-8859-16 |
|
ISO-8859-8 |
|
|
|
Таким образом, слово "tá" может быть декодировано целым рядом различных способов в зависимости от применяемого варианта ISO 8859. Именно по этой причине исследователи должны убедиться, что они для начала определили правильную кодировку, прежде чем пытаться расшифровать текст; в противном случае результат может сильно отличаться от первоначального предполагаемого значения.
Стандарт ISO 8859 был введён для преодоления ограничения ASCII в 128 символов, но этого оказалось недостаточно. В предыдущем разделе было показано, как стандарт ISO 8859 можно применять для представления европейских языков (и слегка более восточных). Однако восточные языки создают дополнительные трудности. Рассмотрим китайский язык, таблица наиболее часто используемых иероглифов современного Китайского языка содержит 7000 символов, в то время как Большой свод китайских иероглифов содержит 54 678 символов. Даже наименьшее из этих двух значений существенно превышает доступные в любой из кодировок ISO-8859 256 символов. Восточным языкам для представления своих языков недостаточно системы ISO-8859. Требуется нечто более масштабное. И именно это появилось в виде unicode.
Основная цель unicode - объединить все предыдущие кодировки и добавить поддержку всех языков, математических символов, эмодзи и т.д. На момент написания этих строк было определено почти 150 000 кодовых пунктов unicode. Максимальное количество возможных кодовых пунктов в unicode равно 0x10FFFF (1 114 111d). Первоначальная, выпущенная в октябре 1991 года, версия unicode содержала чуть более 7000 версия unicode символов. Кодовые пункты unicode предоставляют уникальный числовой идентификатор для каждого из определённых им символов. Независимо от операционной системы, языка и т.д., уникальный идентификатор (также называемый кодовым пунктом) будет постоянным. Это должно было решить все проблемы с кодированием сообщений, но, к сожалению, привело к возникновению ещё одной проблемы.
Листинг 3.7 отражает возможное кодирование слова Hello в unicode.
Листинг 3.7. Возможное кодирование Hello в unicode с применением трёх байт для каждого символа
0000: 0000 4800 0065 0000 6C00 006C 0000 6F ..H..e..l..l..o
В Листинге 3.7 мы немедленно выявляем непосредственную проблему в такой схеме кодирования unicode, ибо для множества символов (всех символов английского алфавита, части символов европейских алфавитов, всех знаков препинания, цифр и т.п.) требуется лишь один байт, но при этом запоминаются три байта. В примере Листинга 3.7 необходимо 15d байт дискового пространства, из которых лишь 5 не равны нулю. Хотя объём дискового пространства не столь ценен как на заре вычислительной техники, это всё же не очень действенное применение пространства. Для решения такой задачи были введены функции преобразования unicode. Они получают пункт кодирования unicode и преобразовывают его таким образом, что он (как правило) занимает в памяти меньше места, нежели при простом применении кодового пункта. Две наиболее часто встречающиеся функции преобразования это UTF-8 (наиболее распространён в Интернете) и UTF-16 (наиболее распространён в продуктах Microsoft). В последующих двух разделах мы более подробно рассмотрим эти функции. Прочие функции преобразования содержат UTF-32, в котором всякий символ представлен четырьмя байтами! Именно такая неэффективность служит той причиной, по которой UTF-32 встречается крайне редко. Ещё одна функция преобразования носит название UCS-2 (Universal Coded Character Set), которая представляет собой двухбайтовую кодировку, способную представлять первые 65 535d кодовых пунктов unicode. И снова, невозможность представления всего диапазона кодовых пунктов является основной причиной того, что UCS-2 более не применяется.
UTF-8 это схема кодирования символа с переменной длиной, которая преобразовывает пункты кода unicode в значения с размером от одного до четырёх байтю Она способна представлять все 0x10FFFF возможные кодовые пункты (CP) unicode и фактически превратилась в стандарт кодирования в Интернете. Одним из основных преимуществ UTF-8 является то, что все основные символы ASCII представлены ровно так же в UTF-8, как они расположены в ASCII - это основная причина того, что так много содержимого Интернета кодируется в UTF-8, поскольку она к тому же содержит также и страницы ASCII.
Таблица 3.10 показывает как кодовые пункты unicode кодируются при помощи UTF-8. Соответствующие x представляют значимые биты реального кодового пункта unicode. Один байт способен представлять самые первые 128d символов (то есть, символы ASCII). Следующие 1920d символов могут быть представлены двумя байтами и так долее. Вероятно, проще всего пояснить Таблицу 3.10 на неком примере. Рассмотрим кодовый пункт unicode 0xE1 (символ á), приводимые ниже шаги демонстрируют как это представляется в UTF-8.
-
Преобразовываем 0xE1 в двоичное представление: 0b1110 0001.
-
Получаемое в результате двоичное представление обладает 8d битами, а следовательно требуется строка 2 Таблицы 3.10(максимальная длина кодового пункта составляет 11d бит, в то время как в первой строке лишь 7d бит).
-
Заполняем своё двоичное значение так, чтобы оно содержало максимально допустимую длину бит (в данном случае 11d бит), получаем: 0b000 1110 0001.
-
Вставляем в окончательную последовательность байт полученное двоичное значение с указанными в Таблице 3.10 шаблонами. Эта последовательность байт 110x xxxx 10xx xxxx. Крестики замещаются полученными на Шаге 3 значениями, что даёт: 1100 0011 1010 0001.
-
Выполняем преобразование кодированного двоичного значения UTF-8 в шестнадцатеричное представление, получаем: 0xC3A1.
| Макс. длина CP | Число байт | Байт 1 | Байт 2 | Байт 3 | Байт 4 |
|---|---|---|---|---|---|
7 бит |
1 |
0xxx xxxx |
|
|
|
11 бит |
2 |
110x xxxx |
10xx xxxx |
|
|
16 бит |
3 |
1110 xxxx |
10xx xxxx |
10xx xxxx |
|
21 бит |
4 |
1111 0 xxx |
10xx xxxx |
10xx xxxx |
10xx xxxx |
Для получения из кодированного UTF-8 значения кодового пункта Unicode обращаем приведённый выше процесс. Например, если кодированное UTF-8 значение было 0xC3B8, тогда кодовый пункт unicode можно найти воспользовавшись таким методом:
-
Преобразуем заданное значение UTF-8 в двоичное представление: 0b1100 0011 1011 1000.
-
Из таблицы 3.10 находим, что это двоичное значение удовлетворяет шаблону строки 2: 1100 0011 1011 1000.
-
Удаление бит найденного шаблона приводит к 0b000 1111 1000.
-
Удаляем первые нулевые биты и получаем: 0b1111 1000.
-
Преобразовываем в шестнадцатеричное (0xF8) и отыскиваем его в таблице кодовых пунктов, что даёт символ: ø.
В то время как знание кодирования данных в UTF-8 жизненно важно при работе в Интернете, оно также выступает стандартом кодирования, применяемом в большинстве версий Linux (и множества файловых систем), а следовательно жизненно необходимо для криминалистического анализа Linux.
UTF-16 это другая функция преобразования, которая, как и UTF-8, способна представлять все допустимые кодовые пункты unicode. Для представления всякого кодируемого символа она пользуется одним или двумя 16 битными (два байта) кодовыми элементами. Самые первые 65 536d символа тривиальны для представления, это всего лишь два байта представления их значения кодового пункта unicode. (Значения кодовых пунктов из диапазона 0xD800–0xDFFF не представлены в UTF-16, так как они применяются в представлении кодовых пунктов, требующих более двух байт. Тем не менее, значения кодовых пунктов 0xD800–0xDFFF не применяются как кодовые пункты unicode - и никогда не будут применяться таковыми - по причине их применения в самой схеме кодирования UTF-16.) Рассмотрим два показанных в предыдущем разделе символа, á и ø с кодовыми пунктами 0xE1 и 0xF8, соответственно, их представлениями UTF-16 будут, соответственно, 0x00E1 и 0x00F8. Помните, что UTF-16 должен применять для представления символа два или четыре байта.
Но что произойдёт в случае, когда размер кодового пункта символа больше двух байт в длину (то есть, больше 0xFFFF)? В таком случае используются два элемента кодирования по 16 бит, которые совместно носят название заменяющей пары (surrogate pair), такой как 0x1F5A5 (иконка настольного компьютера), используется такой метод:
-
Вычитаем из значения кодового пункта нашего unicode (0x1F5A5) значение 0x10000, 0xF5A5.
-
Преобразовываем его в двоичное представление, 0b1111 0101 1010 0101, и, в случае необходимости, дополняем его до 20 бит: 0b0000 1111 0101 1010 0101.
-
Берём самые первые 10 значащих бит (0b00 0011 1101) и преобразовываем из в шестнадцатеричное представление (0x3D), а также добавляем это к 0xD800, получая 0xD83D. Это наш первый кодовый элемент, также имеющий название верхнего заместителя (high surrogate, W1), который всегда находится в диапазоне 0xD800–0xDBFF.
-
Получаем последние 10 значащих бит (0b01 1010 0101) и преобразовываем их в шестнадцатеричное представление (0x1A5), а также добавляем к этому 0xDC00, получая 0xDDA5. Это наш второй кодовый элемент, также называемый нижним заместителем (W2), который всегда пребывает в таком диапазоне (0xDC00–0xDFFF).
-
Для получения окончательного результата сочетаем верхний и нижний заместители (W1 и W2): 0xD83D DDA5.
Как и в случае с UTF-8, когда встречается кодированное в UTF-16 значение, приведённый выше процесс просто обращается. Рассмотрим UTF-16, кодирующий 0xD83C DFC9, для определения значения кодового пункта применяется приводимый ниже метод:
-
Расщепляем на верхний и нижний заместители, получаем 0xD83C (верхний) и 0xDFC9 (нижний).
-
Из нижнего заместителя вычитаем 0xDC00, что приводит к 0x3C9 и преобразуем это к двоичному виду (10 бит), что даёт: 0b11 1100 1001.
-
Из верхнего заместителя вычитанием 0xD800 получаем 0x3C, а преобразование в 10 битное двоичное представление приводит к 0b00 0011 1100.
-
Сочетание этих значений получает 0b0000 1111 0011 1100 1001, а последующее преобразование к шестнадцатеричному имеет результатом 0xF3C9.
-
Добавляя к 0xF3C9 0x10000, чтобы получить 0x1F3C9, что и является значением кодового пункта unicode для знака мяча регби.
Хотя UTF-16 не имеет прямого отношения ко всем ситуациям (точно так же, как популярность UTF-8 основана на его проникновении в тексты Интернета), он часто встречается в семействе продуктов Microsoft (и, в частности, по причине распространённости документов Office, его можно встретить в любой операционной системе), а в качестве кодировки по умолчанию применяется в некоторых языках программирования, например, в Python (определённые версии) и Java. Следовательно, данные в формате UTF-16 могут встречаться в любой анализируемой системе.
Время это фундаментальное понятие при любых расследованиях. По телевизору показывают, как детективы пытаются установить время смерти жертвы убийства. Они спрашивают подозреваемых: "Где вы были в полночь?" Традиционно информация о времени получалась при помощи часов, интерпретировалась людьми и предоставлялась правоохранительным органам как часть свидетельских показаний.
Вычислительная система располагает доступным исследователю обширным массивом данных о времени. Для верной обработки этих сведений требуется целиком разбираться в том, как именно время представлено в вычислительной системе, а также наличие навыков интерпретации данной информации.
Когда мы представляли понятие полей бит, мы ознакомили вас с датой и временем в FAT. Это наиболее старая концепция представления времени и она больше не применяется в современных системах. (Это вовсе не означает, что более не требуется знание даты и времени в FAT. Хотя большинство современных систем больше и не применяют такой способ представления времени, файловая система FAT по- прежнему часто встречается в расследованиях. Многие съёмные устройства по- прежнему пользуются данной системой для хранения сведений о времени. Самая последняя версия для съёмных носителей, ExFAT, также применяет эту систему, хотя она и включает в себя компоненты миллисекунд и часовых поясов.) Обычно современные системы используют значения времени, основанные на эпохах.
Основанные на эпохах системы это всего- навсего счётчики. Они ведут отсчёт через определённые промежутки времени, начиная с конкретно выбранного момента времени. Для их интерпретации необходимо знать эпоху, с которой был начат отсчёт (то есть, нулевое время), а также частоту отсчётов (порой носящей название степени детализации). В Таблице 3.11 приведены некоторые из наиболее распространённых систем временных меток на основании эпох, которые применяются в современных вычислительных системах.
| Время | Эпоха | Степень разбиения | Замечания |
|---|---|---|---|
Windows/NTFS |
|
|
Применяется в ОС Windows и в файловой системе NTFS. Это один из наиболее часто встречающихся в цифровых расследованиях форматов времени. |
Время Unix |
|
|
Применяется во всех системах/ файловых системах Unix. Попадается в ряде артефактов браузеров и прочих приложений. |
Web-kit/Chrome |
|
|
Используется в браузере Google Chrome. |
Время Mac/HFS+ |
|
|
Применяется в файловой системе HFS+ Apple. |
Обычно время Unix часто встречается в системах Unix/ Linux (включая файловые системы), а также и во всём компьютерном мире, и в ряде файловых систем Apple, и в ряде приложений прочих операционных систем. Поэтому в нашем следующем разделе будет подробно рассмотрен формат времени Unix.
Как указано в Таблице 3.11, время Unix основывается на эпохе с 1 января 1970, начавшейся в 00:00:00 UTC. Это нулевое время для времяисчисления Unix. Счётчик увеличивается каждую секунду. Следовательно, в действительности, время Unix измеряет число секунд, истекших с 1 января 1970. Время Unix это время UTC, значение времени UTC всегда хранится как UTC. ОС впоследствии применяет локальные настройки для отражения времени UTC во временной зоне системы.
С точки зрения исследования, важна величина детализации базовой метки времени Unix. Счётчик обновляется раз в секунду. Это означает, что две выполняющиеся в одну и ту же секунду операции будут иметь одинаковую временную метку. Хотя для файлов, к которым пользователь обращается напрямую (люди могут способны за 1 секунду открыть лишь небольшое число файлов), это и не является серьёзной проблемой, автоматизированные процессы за одну секунду могут получать доступ к большому числу файлов. Эти действия нельзя упорядочить. Обратите внимание, что большинство современных реализаций Unix Time включают в себя подчинённый компонент nano-second, позволяющий повышать степень детализации. Это можно увидеть в Листинге 3.8.
Листинг 3.8. Вывод команды istat для EXT2 и EXT4
EXT 2
Inode Times:
Accessed: 2021-01-12 10:19:52 (GMT)
File Modified: 2021-01-12 09:48:43 (GMT)
Inode Modified: 2021-01-12 09:53:03 (GMT)
EXT 4
Inode Times:
Accessed: 2021-06-06 08:17:02.191048178 (IST)
File Modified: 2021-05-21 06:29:30.037357544 (IST)
Inode Modified: 2021-05-21 06:29:30.037357544 (IST)
File Created: 2021-05-21 06:23:31.291162553 (IST)
Листинг 3.8 отражает разницу в величине детализации временных меток при сопоставлении более старой файловой системы Linux (ext2) с более новой файловой системой (ext4). В ext2 применяются значения традиционного времени Unix, что подразумевает степень детализации в одну секунду. В ext4 присутствует добавленный компонент наносекунды, который также обрабатывают инструменты криминалистики. Это означает, что в такой файловой системе можно лучше определять порядок операций. (Вы также могли обратить внимание на то, что имеется отличие в приводимых записанных временных метках. Ext2 записывает времена Изменения файла и inode, а также Доступа. Ext4 записывает эти три временные метки, а также временную метку Создания. Обе файловые системы к тому же записывают временную метку Удаления, но она устанавливается только когда данный файл удалён.)
Время Unix традиционно хранится как 32- битное число без знака. Это подразумевает, что самое большое время, которое можно представить, это 231 - 1. Эта величина, 2 147 483 647d, представляет 2038-01-19 03:14:07 UTC. Именно это значение являет собой самое последнее время, которое может быть представлено традиционной меткой времени Unix. Когда ваш компьютер попытается увеличить значение счётчика на единицу, он "провернётся обратно", что в результате приведёт к времени 1901-12-13 20:45:52 UTC. Данную проблему обычно именуют проблемой Y2038 (а иногда Epochalypse! - коллапсом эпохи). В последние годы многие системы начали пользоваться для представления значения времени Unix 64- битным целым без знака. Это означает, что самое большое возможное значение времени 263 - 1, то есть 9 223 372 036 854 775 807d. Оно не истечёт вплоть до 11 апреля 2262 в 23:47:16 (UTC). Можно с уверенностью сказать, что я здесь точно буду отсутствовать, когда закончится срок действия 64-разрядной версии Unix!
Чтобы мы имели возможность обрабатывать значения времени эпохи Unix, оболочка Linux снабжает нас командой date. Листинг 3.9 показывает нам эту команду для определения текущего значения времени эпохи Unix.
Листинг 3.9. Применение команды date для отображения текущего значения времени Unix.
$ date '+%s'
1623060055
Листинг 3.10 как воспользоваться командой dateдля преобразования временной метки Unix в воспринимаемый людьми формат.
Листинг 3.10. Применение команды date для преобразования времени Unix в воспринимаемый людьми формат.
$ date -d @1623060055
Mon 07 Jun 2021 11:00:55 IST
Обратите внимание на то, что в Листинге 3.10 значение времени приводится в IST (Irish Summer Time). Оно применяется нашей ОС, пользующейся текущими локальными настройками той машины, на которой мы выполнили свою команду. Листинг 3.11 отображает команду date , применяемую для отображения значения времени в UTC (выступающем точной хранимой в вашей файловой системе датой).
Листинг 3.11. Применение date для отображения времени Unix в UTC.
$ date -ud @1623060055
Mon 07 Jun 2021 10:00:55 UTC
В процессе расследования зачастую требуется отображать времена для прочих временных зон. Этого можно достичь воспользовавшись TZ=, как это показано в Листинге 3.12, где предшествующая команде date директива TZ=US/Eastern изменяет отображаемый часовой пояс.
Эта глава изучала как в вычислительных системах представляются данные, однако самая основная цель данной главы состоит в том, чтобы предоставить возможность интерпретации сырых данных. В то время как жизненно важно понимать как информация представляется нулями и единицами, также необходимо разбираться в том как она хранится в вычислительных системах, прежде чем она будет точно интерпретирована.
В целом, существует два применяемых компьютерами метода для хранения информации: либо формат обратного (big-endian) следования байт, либо формат прямого (little-endian) следования байт. Эти порядки следования байт описывают как следует считывать всю информацию. Рассмотрим естественные языки, английский и арабский, в английском мы читаем слева направо, в то время как в арабском чтение происходит справа налево. Эти языки можно считать как обладающие разным порядком следования.
При формате обратного порядка (big-endian) следования наиболее значимый байт хранится первым, затем идёт следующий менее значимый байт и так далее, пока не будет достигнут наименее значимый байт. При схеме с прямым порядком следования (little-endian) первым хранится наименее значимый байт, за ним следует второй менее значимый байт и так далее, все вплоть до заключительного байта, которым выступает наиболее значимый байт. В этой главе, вплоть до данного момента, все встречавшиеся нам данные были представлены в формате обратной последовательности.
Рассмотрим число 56 000d. После его преобразования в шестнадцатеричный вид это 0xDAC0. Что автоматически выступает значением с обратным порядком следования. Байт 0xDA это наиболее значимый байт и он хранится первым, а байт 0xC0 это наименее значимый и хранится последним. Если бы применяемый метод хранения был бы с прямой последовательностью, порядок следовало бы изменить, что означает, что в сырых данных мы бы встретили значение 0xC0DA. Теперь рассмотрим значение 400 000 000d. В шестнадцатеричном представлении это 0x17D78400. Это значение с обратным порядком следования. Его преобразование в значение с прямым порядком следования выполняется следующим образом (отметим, что для ясности добавлены пробелы):
Big-Endian (обратный порядок) 17 D7 84 00
Little-Endian (прямой порядок) 00 84 D7 17
Именно это является заключительным из необходимых для интерпретации информации фрагментом. Рассмотрим шестнадцатеричный дамп, показанный в Листинге 3.13. Здесь отражена таблица разделов главной загрузочной записи (MBR, Master Boot Record) для физического диска и применяемая для её извлечения команда Linux. Данная таблица разделов состоит из четырёх 16- байтовых записей, причём каждая из них отражается по одной строчке вниз.
Листинг 3.13. Отображение содержимого таблицы разделов первичного диска (/dev/sda.)
# xxd -s 446 -l 64 /dev/sda
001be: 8020 2100 07df 130c 0008 0000 0020 0300 . !.......... ..
001ce: 00df 140c 07fe ffff 0028 0300 c296 ce22 .........(....."
001de: 00fe ffff 27fe ffff 00c0 d122 0098 1100 ....’......"....
001ee: 00fe ffff 05fe ffff fe67 e322 0200 8d51 .........g."...Q
Тем не менее, как и для всех сырых данных, без знания лежащих в их основе структур, практически невозможно интерпретировать такие данные. Структура для таблицы разделов приведена в Таблице 3.12. Обратите внимание, что все значения со множеством байт хранятся в прямом порядке последовательности!
| Смещение | Размер | Описание |
|---|---|---|
|
|
Состояние возможности загрузки - 0x00 для раздела без возможности загрузки, 0x80 для загружаемого раздела. |
|
|
CHS (Cylinder-head-sector, цилиндр-головка-сектор) для самого первого сектора в данном разделе. Это старая форма адресации, которая была заменена значениями логического адреса и размера. |
|
|
Идентификатор типа раздела - 0x07 это NTFS; 0x0B это FAT 32; 0x83 это Linux, и т.д. Полный перечень этих кодов можно найти в Интернете, например. |
|
|
CHS (Cylinder-head-sector, цилиндр-головка-сектор) для самого последнего сектора в данном разделе. Это старая форма адресации, которая была заменена значениями логического адреса и размера. |
|
|
LBA (Logical block address, адрес логического блока) для самый первый абсолютный сектор в данном разделе. Это современная форма адресации, которую следует применять вместо адресов CHS. |
|
|
Число секторов в разделе. |
Листинг 3.14 показывает самую первую запись таблицы разделов с выделенными подчёркиванием альтернативными полями. Эти поля основываются на комбинации смещение/ размер из Таблицы 3.12. Например, значение LBA для данного раздела начинается со смещения 0x08 и имеет размер 0x04 байт. Это означает, что соответствующие хранимые в этом месте сырые данные это: 0x0008 0000.
Листинг 3.14. Самая первая запись таблицы разделов из Листинга 3.13 с выделенными альтернативными полями.
# xxd -s 446 -l 64 /dev/sda
001be: 8020 2100 07df 130c 0008 0000 0020 0300 . !.......... ..
Из листинга 3.14 ясно, что данный раздел загружаемый (0x01 байт со смещением 0x00) и его тип 0x07 (0x01 байт со смещением 0x04), иначе говоря, файловая система NTFS. (Обратите внимание, что при криминалистическом анализе указанное для типа файловой системы в таблице разделов значение не является надёжным. Для определения точного типа файловой системы необходимо изучить содержимое самого раздела.) Стартовый адрес LBA задаётся 0x04 байтами по смещению 0x08, и это значение 0x0008 0000; однако это прямой порядок следования, что подразумевает, что первым хранится наименее значимый байт. Перед проведением процедуры преобразования в десятичное значение его необходимо конвертировать в обратный порядок следования.
Big-Endian (обратный порядок) 00 08 00 00
Little-Endian (прямой порядок) 00 00 08 00
Это означает, что реальным значением LBA выступает 0x800 или 2048d. Аналогичный процесс выполняется для величины размера этого раздела. Он находится в четырёх байтах по смещению 0x0C, которые обладают значением прямого порядка следования 0x00 20 03 00. Преобразование этого в обратный порядок следования даёт нам 0x00 03 20 00, что равно размеру в 204 800d секторов. Тем самым мы вручную интерпретировали эту запись таблицы разделов, обнаружив, что данный раздел начинается с сектора 2048d и обладает размером в 204 800d секторов. Это именно тот метод, который применяется инструментами криминалистики при считывании имеющейся таблицы разделов. Рассмотрим вывод из криминалистического инструмента файловой системы с названием mmls (который мы рассматриваем в Главе 4), что отражено в Листинге 3.15. Данный инструмент выдаёт сведения, идентичные полученным нами вручную выше.
Листинг 3.15. Применение mmls для подтверждения полученных при ручной интерпретации первой записи таблицы разделов из Листинга 3.14. Отражены лишь относящиеся к делу моменты, остальной вывод mmls опущен.
# mmls /dev/sda
Slot Start End Length Description
...[snip]...
002: 000:000 00002048 00206847 00204800 NTFS / exFAT (0x07)
...[snip]...
В данной главе приведены необходимые для цифровой криминалистики предварительные математические сведения. Предполагается, что читатель знаком с этими понятиями, и они лишь служат напоминанием. Основным типом данных в компьютере и в электронных системах хранения/передачи является бит. Единственная двоичная цифра способна принимать значения ноль или единица, из которых состоят все сложные типы, с которыми мы сталкиваемся в вычислительной системе.
С точки зрения интерпретации исходных данных, как правило, наиболее важно, чтобы числовые, текстовые и данные времени можно было интерпретировать точно. Особое значение это имеет в файловых системах Linux, где не обязательно имеются инструменты для их обработки. Следовательно, иногда требуется выполнить анализ вручную, как это показано на примере записей таблицы разделов главной загрузочной записи (MBR) (раздел 3.5). Например, любыми инструментами судебной экспертизы поддерживается лишь файловая система ext Linux, но в системах Linux порой встречаются и иные файловые системы, такие как XFS, BtrFS и ReiserFS. На момент написания этой статьи не существовало инструментов криминалистики, которые поддерживали бы эти файловые системы полностью.
-
Преобразуйте следующие числа в десятичные:
-
0x4A
-
0x1CD
-
0b101101
-
0b11001001
-
-
Преобразуйте приводимые далее числа в двоичные:
-
0x3D1
-
0xBAD
-
0d123
-
0d42
-
-
Конвертируйте числа ниже в шестнадцатеричные:
-
0b01011010
-
0b1100011
-
0d193
-
0d72
-
-
Каковы десятичные значения следующих 8- битных чисел в дополнительном коде?
-
0b01101100
-
0b11100100
-
0b11001111
-
0b10011000
-
-
Приводимые далее шестнадцатеричные последовательности представляют текст ASCII. Что они означают?
-
4865 6C6C 6F20 576F 726C 64
-
4C69 6E75 7820 466F 7265 6E73 6963 730A
-
-
Декодируйте идущие следом Кодовые пункты inicode как (i) UTF-8; (ii) UTF-16
-
Кодовый пункт: 0x0398 – Заглавная греческая буква тетта
-
Кодовый пункт: 0x1F3A7 – Эмодзи наушников
-
Кодовый пункт: 0x1F415 – Эмодзи собаки
-
-
Какие символы представлены следующими кодированными обратной последовательностью значениями UTF-8?
-
0xCE94
-
0xE29A99
-
0xF09FA68D
-
-
Какие символы представлены следующими кодированными обратной последовательностью значениями UTF-16?
-
0x03A3
-
0xD83CDF40
-
0xD83CDF69
-
-
В Разделе 3.5 проведена интерпретация первой из четырёх записей таблицы разделов. Сделайте разбор оставшихся трёх записей таблицы разделов.
File System Forensic Analysis. Carrier, B. (2005). Boston, MA, London: Addison-Wesley {github}
Computer Organisation and Architecture, Chalk, B.S., Carter, A., and Hind, R. (2017). Bloomsbury Publishing.
What every computer scientist should know about floating-point arithmetic. Goldberg, D. (1991). ACM Computing Surveys (CSUR) 23 (1): 5–48.
Digital Design and Computer Architecture. Harris, S.L. and Harris, D.M. (2016). Amsterdam, Paris: Elsevier, Cop.
The IEEE Standard 754: one for the history books. Hough, D.G. (2019). Computer 52 (12): 109–112/ IEEE STD 754-2019 (2019). The IEEE Standard 754: one for the history books. IEEE Standard for Floating-Point Arithmetic. IEEE Computer Society, pp. 1–84.
Disclosure in criminal cases. Citizensinformation.ie (2024). по состоянию на 29.03.2025.
ISO/IEC 646:1991 Information Technology - ISO 7-Bit Coded Character Set for Information Interchange, International Standards Organization (1991). Geneva, Switzerland: International Standards Organization.
ISO/IEC 8859-1 Information Technology - 8-Bit Single Byte Coded Graphic Character Sets International Standards Organization (1998). Geneva, Switzerland: International Standards Organization.
ISO/IEC 10646:2020 Information Technology - Universal Coded Character Sets. International Standards Organization (2020). 6e. Geneva, Switzerland: International Standards Organization.
Lecture Notes on the Status of IEEE Standard 754 for Binary Floating-Point Arithmetic. Kahan, W. (1996).
What is Copyleft?. gnu.org (2024). по состоянию на 29.03.2025
Art of Computer Programming, vol. 2. Knuth, D.E. (2014). Addison-Wesley Professional, pdf, Вильямс.
Handbook of Floating-Point Arithmetic. Muller, J.M. (2018). Boston, MA: Birkhäuser.
Linux Bible Negus, C. (2020). Wiley & Sons Canada, Limited, John.
Unicode® 15.0.0. The Unicode Consortium (2023). www.unicode.org. [по состоянию на 13.04.2025].