Глава 3. Форматы файлов
Содержание
Обсудив основы семантики B- деревьев, мы теперь готовы к изучению того как именно реализовать на диске B- деревья и прочие структуры. Мы получаем доступ к диску другим способом по сравнению с тем как мы выполняем доступ в основной памяти: с точки зрения разработчика приложения, доступ в памяти в целом прозрачен. Благодаря виртуальной памяти [BHATTACHARJEE17], нам не требуется управлять вручную смещениями. Доступ к дискам выполняется при помощи системных вызовов (см. https://databass.dev/links/54). Обычно нам приходится определять значение смещения внутри своего целевого файла, а затем интерпретировать представление на диске в некий вид, подходящий для основной памяти.
Это означает, что действенные дисковые структуры необходимо разрабатывать с таким отличием в уме. Для этого нам приходится обращаться к форматам файлов, которые просто конструировать, изменять и интерпретировать. В данной главе мы обсудим общие принципы и практические приёмы, которые помогут нам проектировать все виды дисковых структур, причём не только B- деревья.
Для реализации B- деревьев существует множество возможностей и здесь я обсуждаю несколько полезных технологий. Поробности могут варьироваться между реализациями, однако общие принципы остаются теми же. Понимание базовой механики B- деревьев, такой как расщепления и слияния является необходимым, однако этого недостаточно для реальной реализации. Имеется множество моментов, которым следует вступать в игру сообща для того чтобы окончательный результат был полезным.
Сама семантика управления указателями в дисковых структурах нечто совершенно иное по сравнению с указателями в памяти. Полезно представлять себе дисковые B- деревья как некий механизм управления страницами: алгоритмам приходится составлять страницы и выполнять по ним навигацию. Страницы и указатели на них должны вычисляться и размещаться надлежащим образом.
Поскольку основная сложность B- деревьев проистекает из изменчивости, мы обсудим подробности выкладки страниц, их расщепления, перемещения и прочие понятия, применяемые к изменяемым структурам данных. Позднее, при обсуждении Деревьев LSM (см. раздел Деревья LSM), мы сосредоточимся на сортировке и сопровождении, так как именно отсюда проистекает основная сложность LSM.
Создание некого формата файла во многом аналогично тому как мы создаём структуры данных в языках программирования при некой неуправляемой модели памяти. Мы выделяем некий блок данных и нарезаем его любым способом, которым пожелаем, применяя примитивы и структуры фиксированного размера. Когда мы желаем ссылаться на больший фрагмент памяти или на некую структуру переменной длины, мы пользуемся указателями.
Языки программирования с неуправляемой моделью памяти позволяют нам выделять дополнительную память в любой момент времени, когда она нам потребуется (в рамках разумных ограничений) без того чтобы задумываться или беспокоиться относительно того будет или нет доступен непрерывный сегмент памяти, будет ли он фрагментирован или нет, или что произойдёт после того как мы освободим его. На диске нам приходится заботиться о сборке мусора и фрагментации самостоятельно.
Планирование данных в памяти намного менее важно нежели на диске. Для эффективности обитающей на диске структуры данных нам требуется располагать данные на диск таким образом, чтобы делать к ним возможным быстрый доступ и принимать во внимание сами особенности носителя постоянного хранения доходить до двоичных форматов данных и находить действенные средства сериализации и обратного разбора данных.
Всякий кто когда- либо пользовался языками нижнего уровня, такими как C без дополнительных библиотек знаком с имеющимися ограничениями. Структуры имеют некий предварительно заданный размер и выделяются и высвобождаются в явном виде. Выделение и отслеживание памяти, реализуемое вручную, даже ещё больший вызов, так как позволяет работать исключительно с сегментами памяти предварительно заданного размера и необходимо отслеживать какие сегменты уже высвобождены, а какие всё ещё используются.
При хранении данных в основной памяти большинства проблем со схемой памяти не существует, их проще решать или они могут быть решены при помощи библиотек сторонних производителей. Например, обработка полей переменной длины и имеющих большой размер данных намного более непосредственная, так как мы можем применять выделение в памяти и указатели и нам не требуется выкладывать их неким особым образом. Всё ещё имеются ситуации, при которых разработчики проектируют особые схемы данных основной памяти для получения преимущества линий кэширования ЦПУ, предварительной выборки и прочих относящихся к оборудованию особенностей, но в целом это делается для целей оптимизации [FOWLER11].
Даже хотя имеющиеся операционная система и файловая система принимают на себя часть ответственности, реализация дисковых структур требует внимания к дополнительным подробностям и имеет гораздо больше ловушек.
Для действенного сохранения данных на диск их необходимо кодировать при помощи некого формата, который является компактным и прост для сериализации и обратной процедуры. При обсуждении двоичных форматов вы достаточно слышите слова схема размещения (layout). Поскольку у нас нет подобных malloc и free примитивов, а лишь read и write, нам приходится думать о доступе иначе и готовить данные соответствующим образом.
Здесь мы обсудим самые основные принципы, применяемые для создания эффективных схем размещения страниц. Эти принципы применимы к любому двоичному формату: вы можете использовать аналогичное руководство для создания файла и форматов сериализации или протоколов взаимодействия.
Прежде чем мы сможем организовать записи на страницах, нам требуется осознать как представлять ключи и записи данных в двоичном виде, как комбинировать множество значений в более сложные структуры и как реализовывать типы и массивы переменной длины.
Ключи и значения обладают неким типом, таким как
integer, date или
string, и могут быть представлены в(последовательно или параллельно) в виде
своих сырых двоичных значений.
Большинство численных типов данных представляются в виде значений фиксированной длины. При работе с численными данными со множеством байт важно применять один и то же порядок байт (endianness), причём как для кодирования, так и для декодирования. Порядок следования байт определяет саму последовательность байт:
- Big-endian
Этот порядок начинается с наиболее значимого байта (MSB, most-significant byte), за которым следуют байты в порядке убывания значимости. Иными словами, MSB имеет наинизший адрес.
- Little-endian
Данный порядок стартует с наименее значимого байта (LSB, least-significant byte), за которым байты в возрастающем порядке значимости.
Рисунок 3-1 иллюстрирует это. Наше шестнадцатеричное 32- битное целое 0xAABBCCDD,
где AA это SB, показано как с применением порядка байт big-, так и с
little- endian.
Рисунок 3-1

Big- и little- endian порядки байт. Наиболее значимый байт показан серым. Адресация, обозначаемая
a, растёт слева направо.
Например, для реконструкции некого 64- битного целого в соответствующем порядке байт RocksDB имеет специфичное для
платформы определение, которое помогает указывать цель порядка байт платформы (В зависимости от выбранной платформы - macOS, Solaris, AIX или одно из предпочтений
BSD, либо Windows - значение переменной kLittleEndian) устанавливается в
зависимости от того будет или нет эта платформа поддерживать little-endian. Когда данная целевая платформа не
соответствует значению порядка следования байт (EncodeFixed64WithEndian просматривает значение kLittleEndian и
сравнивает его с порядком следования байт), он меняет местами порядок байт при помощи
EndianTransform, который способен считывать
байтовые значения и изменять на обратный их порядок, добавляя их в конец получаемого результата.
Записи состоят из таких примитивов как числа, строки, булевы значения и их сочетания. Однако, при передаче данных через сетевую среду или при сохранении на диск, мы можем применять только последовательности байт. Это означает, что для отправки или сохранения записи нам приходится выполнять её сериализацию (преобразование в некую непрерывную последовательность байт) и, прежде чем мы сможем использовать её после получения и считывания, нам придётся выполнить обратную процедуру (deserialize) с ней (перевести в последовательность байт, обратно в первоначальный порядок записи).
В двоичных форматах данных мы всегда начинаем с примитивов, которые служат в качестве строительных блоков для
более сложных структур. Различные типы могут меняться по размеру. Значение byte
состоит из 8 бит, short из 2 байт (16 бит), int
из 4 байт (32 бит), а long из 8 байт (64 бит).
Числа с плавающей запятой (например, float и double)
представлены своими знаком, Italic
и дробной частью и показателем степени.
Стандарт IEEE Standard for Binary
Floating-Point Arithmetic (IEEE 754) описывает широко распространённые представления чисел с плавающей запятой.
Некое 32- битное float представляет значение с одинарной точностью. Например,
число с плавающей запятой 0.15652 обладает двоичным представлением, показанном
на Рисунке 3-2. Самые первые 23 бита представляют дробную часть, последующие 8 бит представляют показатель степени, а
1 бит представляет знак (является или нет это число отрицательным).
Так как значение с плавающей запятой вычисляется при помощи дробной части, это число даёт представление лишь некого приближения. Обсуждение полного алгоритма преобразования выходит за рамки данной книги и мы лишь рассматриваем основы его представления.
Величина double представляет значение с плавающей запятой двойной
точности [SAVARD05]. Большинство языков программирования
обладают средствами для кодирования и декодирования значений с плавающей запятой в их двоичное представление и
обратно в своих стандартных библиотеках.
Все типы числовых примитивов имеют некий фиксированный размер. Составление более сложных значений воедино во многом
схоже со struct в C (Будет не лишним отметить, что компиляторы могут добавлять
в структуры заполнение. Это может нарушать наше предположение о точных значениях смещений байт и их места. Вы можете
ознакомиться со структурами упаковки дополнительно здесь). Вы можете сочетать значения примитивов в структуры и применять массивы фиксированного
размера или указатели на прочие области в памяти.
Строки и прочие типы данных переменной длины (такие как массивы данных с фиксированным размером) могут подвергаться
сериализации как некие числа, представляя значение длины такого массива или строки с последующим
size байт: реальными данными. Для строк такое представление часто именуется как
Строки UCSD или Строки Pascal, носящие название в честь популярной реализации языка программирования Pascal.
Мы можем выразить это в псевдокоде следующим образом:
String
{
size uint_16
data byte[size]
}
Некой альтернативой для строк Pascal являются завершающиеся нулём строки, в
которых считывание потребляет такую строку байт пока не будет достигнут символ конца строки. Подход строк Pascal
обладает определёнными преимуществами: он позволяет определять длину строки за постоянное время вместо выполнения
итераций по содержимому строки, а некая особая для языка программирования строка может составляться разделением
size байт в памяти и пересылкой полученного массива байт в некий построитель
строки.
Булевы значения могут представляться либо при помощи отдельного байта, либо кодированием true
и false как значений 1 и
0. Поскольку булевы имеют лишь два значения, применение целого байта для его
представления расточительно и разработчики часто собирают булевы значения вместе в группы по восемь, причём каждое булево
занимает всего лишь один бит. Мы говорим что каждый бит 1 это
установка (set), а каждый бит 0
это сброс (unset) или пусто (empty).
Enums, сокращение от enumerated types (перечислимых типов), могут представляться как целые и часто применяются в двоичных форматах и протоколах взаимодействия. Enums используются для представления часто повторяющихся значений с низкой кардинальностью (мощностью). Например, мы можем закодировать тип некого узла B- дерева при помощи enum:
enum NodeType {
ROOT, // 0x00h
INTERNAL, // 0x01h
LEAF // 0x02h
};
Другим тесно связанным понятием являются флаги, некий вид сочетания упакованных булевых и enums. Флаги могут представлять неизменные исключительные именованные булевы параметры. Например, мы можем применять флаги для обозначения того будет или нет данная страница содержать значения ячеек, будут ди такие значения иметь фиксированных размер или переменный размер и будут ли иметься или нет страницы переполнения, связанные с этим узлом. Так как каждый бит представляет некое значение флага, мы можем применять для масок лишь степень двух (так как степень двух в двоичном всегда имеет отдельный бит установки; например, 23 == 8 == 1000b, 24 == 16 == 0001 0000b и т.п.):
int IS_LEAF_MASK = 0x01h; // bit #1
int VARIABLE_SIZE_VALUES = 0x02h; // bit #2
int HAS_OVERFLOW_PAGES = 0x04h; // bit #3
Также как и булевы, значения флагов могут считываться из своего упакованного значения при помощи
битовых масок и побитовых операторов. Например, для установки бита для одного
определённого флага мы можем воспользоваться побитовым OR
(|) и некой битовой маской. Вместо битовой маски мы можем применить
битовый сдвиг (<<) и некий
индекс бита. Для сброса значения бита мы можем воспользоваться побитовым AND
(& и побитовым оператором отрицания (~).
Для проверки того установлено или нет значение бита n, мы можем сравнить
результат побитового AND с 0:
// Установка значения бита
flags |= HAS_OVERFLOW_PAGES;
flags |= (1 << 2);
// Сброс значения бита
flags &= ~HAS_OVERFLOW_PAGES;
flags &= ~(1 << 2);
// Проверка того установлен или нет бит
is_set = (flags & HAS_OVERFLOW_PAGES) != 0;
is_set = (flags & (1 << 2)) != 0;
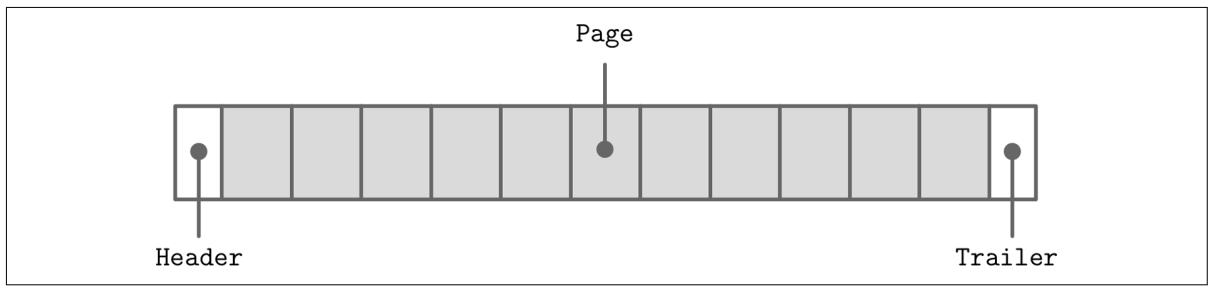
Обычно вы приступаете к проектированию формата файла принимая решение о том как собираетесь осуществлять его адресацию: будет ли этот файл подвергнут расщеплению на страницы того же размера, который представляет отдельный блок или множество непрерывных блоков. Большинство обновляемых по месту содержания данных структур хранения применяют страницы того же размера, так как это значительно упрощает доступ на чтение и запись. Структуры хранения с добавлением только в конец также часто пользуются записью страниц даных: записи добавляются в конец одна за другой, сразу по заполнению страниц в памяти они сбрасываются на диск.
Такой файл обычно начинается с некого заголовка фиксированного размера и может завершаться концевиком (trailer) фиксированного размера, которые содержат вспомогательные сведения, доступ к которым должен осуществляться быстро или же необходим для декодирования оставшейся части данного файла. Весь остаток файла делится на страницы. Рисунок 3-3 схематически отображает организацию такого файла.
Многие хранилища данных обладают некой фиксированной схемой, определяющей общее число, порядок и тип полей, которые способна содержать данная таблица. Обладание некой фиксированной схемой способствует снижению хранимых на диске данных: вместо повторения записи названий полей мы можем применять их позиционные идентификаторы.
Когда вы желаете спроектировать некий формат для каталога своей компании, хранимых имён, дат рождения, налоговых номеров и пола для каждого сотрудника, мы можем применять различные подходы. Мы можем хранить все поля фиксированного размера (такие как дата рождения и налоговый номер) в самом заголовке данной структуры, за которым следуют поля с изменяемым размером:
Fixed-size fields:
| (4 bytes) employee_id |
| (4 bytes) tax_number |
| (3 bytes) date |
| (1 byte) gender |
| (2 bytes) first_name_length |
| (2 bytes) last_name_length |
Variable-size fields:
| (first_name_length bytes) first_name |
| (last_name_length bytes) last_name |
Теперь, для доступа к first_name мы можем отрезать first_name_length
байт после его области физического размера. Для доступа к last_name мы
можем определить его начальное положение проверив значение размера предшествующих ему полей переменного размера.
Во избежание вычислений, включающих в себя множество полей, мы можем закодировать и
смещение и длину, оба значения, на область
фиксированного размера. В таком случае мы можем определять местоположение любого поля переменной длины по отдельности.
Построение более сложных структур обычно вовлекает построение иерархий: поля составляются из примитивов, ячейки составляются из полей, страницы составляются из ячеек, разделы составляются из страниц, области составляются из разделов и так далее. Не существует строгих правил, которым вам тут надлежит следовать, причём все они зависят от того вида данных, для которого вам следует создавать формат.
Файлы баз данных часто состоят из множества частей, причём некая таблица поиска имеет целью навигацию и указание на начало смещений на эти части, записанные либо в заголовке, концевике такого файла, или же в обособленном файле.
Системы баз данных хранят записи данных в файлах данных и индексации. Эти файлы разделяются на элементы фиксированного размера, имеющие название страниц, которые часто имеют размер произведения блоков файловой системы. Обычно страницы находятся в диапазоне от 4 до 16 кБ.
Давайте взглянем на соответствующий образец размещаемого на диске узла B- дерева. С точки зрения некой структуры, в B- деревьях мы имеем отличия между терминальными узлами, которые содержат ключи и записи данных и нетерминальными узлами, которые содержат ключи и указатели на прочие узлы. Каждый узел B- дерева занимает одну страницу или множество связанных воедино страниц, поэтому в контексте B- деревьев сами термины узел и страница (а порой даже блок) часто взаимозаменяемы.
Первоначальная статья B- дерева [BAYER72] описывает
простую организацию страниц для записей данных фиксированного размера, в которых каждая страница это всего лишь
конкатенация триплетов, как это показано на рисунке 3-4: ключи обозначаются как k,
связанные с ними значения как v, а указатели на дочерние страницы
обозначаются как p.
Такой подход прост для его реализации, однако он обладает рядом тёмных сторон:
-
Добавление некого ключа в конец куда угодно, но при этом с правой стороны требует переразмещения элементов.
-
Он не допускает управления или действенного доступа к записям переменного размера и работает лишь с записями фиксированного размера.
При хранении записей переменной длины основная проблема состоит в управлении свободным пространством:
восстановлении того пространства, которое занято удаляемыми записями. Если мы попытаемся поместить запись
с размером n в некое пространство, которое изначально было занято
записью с размером m, пока не выполняется
m == n, или мы не можем отыскать другую запись, которая в точности имеет размер
m - n, это пространство остаётся незанятым. Аналогично, некий сегмент с размером
m не может применяться для хранения записей с размером
k, когда k больше чем
m, поэтому последняя будет вставляться без возврата имеющегося неиспользуемым
пространства.
Для упрощения управления пространством под записи переменного размера мы можем расщеплять свою страницу на сегменты
с фиксированным размером. Однако мы в конце концов когда мы следуем этим путём, мы также получаем трату пространства
впустую. Например, когда мы применяем размер сегмента в 64 байта, пока размер соответствующей записи не является произведением
с 64, мы теряем 64 - (n modulo 64) байт, где n
является размером вставляемой записи. Иными словами, пока запись не кратна 64, один из её блоков будет заполнен лишь
частично.
Возврат пространства можно выполнять путём простой перезаписи данной страницы с перемещением соответствующих записей, но нам потребуется сберегать смещения записи, так как эти смещения могут применять выходящие за страницу указатели. К тому же, желательно это делать с минимальными бесполезными потерями пространства.
Чтобы суммировать, нам необходим некий формат страницы, который позволит нам:
-
Сохранять записи переменного размера с минимальными накладными расходами.
-
Возвращать занимаемое удаляемыми записями пространство.
-
Ссылаться на записи из этой страницы без необходимости заботы о их точном местоположении.
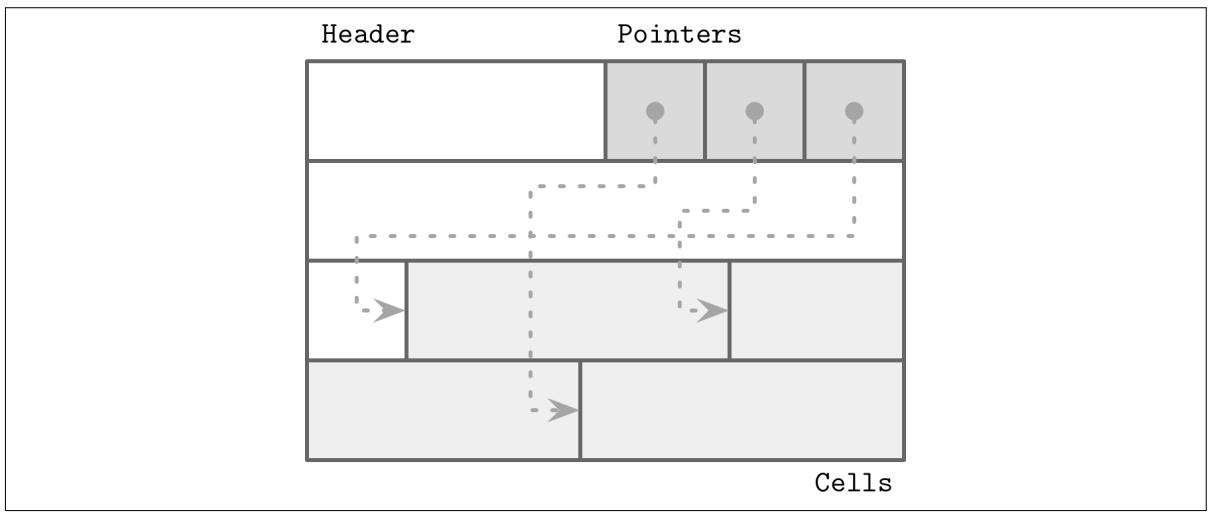
Для эффективного хранения записей переменной длины, таких как строки, BLOB (binary large objects) и т.п., мы можем применять технологию организации с названием Перекидных страниц (то есть страниц с прорезями, slotted page) [SILBERSCHATZ10] или Перекидного каталога [RAMAKRISHNAN03]. Такой подход используется многими базами данных, например, PostgreSQL.
Мы организовываем такую страница как коллекцию раскладушек (slots) или ячеек (cells) и расщепляем указатели и ячейки на две независимые области памяти, располагающиеся на различных сторонах этой страницы. Это означает, что нам лишь требуется повторно организовать адресацию указателей на ячейки для предохранения их порядка, а удаление некой записи может быть выполнено либо обнулением её указателей или их удалением.
Некая перекидная страница обладает заголовком фиксированного размера, который содержит важные сведения относительно самой страницы и её ячеек (см. Заголовок страницы). Ячейки могут отличаться в размере и способны содержать произвольные данные: ключи, указатели, записи данных и т.п.. Рисунок 3-5 отображает организацию Перекидных страниц, при которой каждая страница имеет некую область сопровождения (заголовок), ячейки и указатели на них.
Давайте рассмотрим как этот подход решает обозначенные нами в предыдущем разделе задачи:
-
Минимальные накладные расходы: единственными накладными расходами, вносимыми Перекидными страницами являются связанные с массивом указателей для хранения смещений для точного позиционирования мест нахождения хранимых записей.
-
Возврат пространства: пространство может возвращаться путём деврагментации и перезаписи такой страницы.
-
Динамическая схема: извне данной страницы на такие раскладушки можно ссылаться лишь по их идентификаторам, поэтому знание точного места является внутренним для такой страницы.
Применяя флаги, перечислимые (enums) и примитивные значения, мы можем начинать проектирование схемы ячейки, затем сочетать ячейки в страницу и составлять из таких страниц некое дерево. На уровне некой ячейки у нас имеется разница между ячейками ключей и ключ- значение. Ячейки с ключом содержат некий разделительный ключ и указатель на страницу между двумя соседними указателями. Ячейки ключ- значение содержат ключи и связанные с ними записи данных.
Мы предполагаем, что все ячейки внутри таких страниц единообразные (к примеру, все ячейки могут содержать либо только ключи, либо как ключи, так и значения, но без их перемешивания). Это означает, что мы можем сохранять за один раз описывающие ячейку метаданные вместо того, чтобы дублировать их в каждой ячейке.
Для составления некой ячейки ключей нам требуется знать:
-
Тип ячейки (может подразумеваться по самой странице метаданных)
-
Размер ключа
-
Идентификатор соответствующей дочерней страницы, на которую указывает эта ячейка
-
Байты ключа
Схема ячейки ключа переменной длины может выглядеть подобно этому (ячейка фиксированного размера не будет иметь описателя размера на самом уровне ячейки):
0 4 8
+----------------+---------------+-------------+
| [int] key_size | [int] page_id | [bytes] key |
+----------------+---------------+-------------+
Мы сгруппировали данные с фиксированным размером вместе вслед за байтами key_size.
Строго говоря, это не является обязательным, но может упростить вычисление смещения, так как ко всем полям фиксированного
размера можно получать доступ применяя статические, заранее вычисленные смещения, и нам потребуется вычислять значение
смещений только для имеющихся данных переменной длины.
Ячейки ключ- значение содержат записи данных вместо значений идентификаторов дочерних страниц. Во всём остальном их структура аналогична:
-
Тип ячейки (может подразумеваться по самой странице метаданных)
-
Размер ключа
-
Размер значения
-
Байты ключа
-
Байты записи данных
0 1 5 ...
+--------------+----------------+
| [byte] flags | [int] key_size |
+--------------+----------------+
5 9 .. + key_size
+------------------+--------------------+----------------------+
| [int] value_size | [bytes] key | [bytes] data_record |
+------------------+--------------------+----------------------+
Здесь вы могли заметить основное отличие между значениями смещения и идентификатора страницы. Поскольку страницы обладают неким фиксированным размером и управляются имеющимся кэшем страниц (см. Управление буфером), нам требуется хранить лишь значение идентификатора страницы, который позднее транслируется в реальное смещение в самом файле при помощи таблицы поиска. Смещения ячейки локальны для страницы и отсчитываются относительно начального смещения самой страницы: таким образом мы можем применять меньшую кардинальность целого для удержания представления в более компактном виде.
![[Замечание]](/common/images/admon/note.png) | Данные переменного размера |
|---|---|
|
Для ключа и значения нет необходимости в фиксированном размере. Как ключ, так и значие могут обладать переменной длиной. Их местоположение может вычисляться по заголовку ячейки постоянного размера с применением смещений. Для определения местоположения ключа мы пропускаем установленный заголовок и считываем байты
Существуют различные способы выполнения одного и того же; например, сохраняя общий размер и вычисляя величину размера значения вычитанием. Всё сводится к тому чтобы иметь достаточно сведений для нарезки самой ячейки на составные части и восстановления её закодированных данных. |
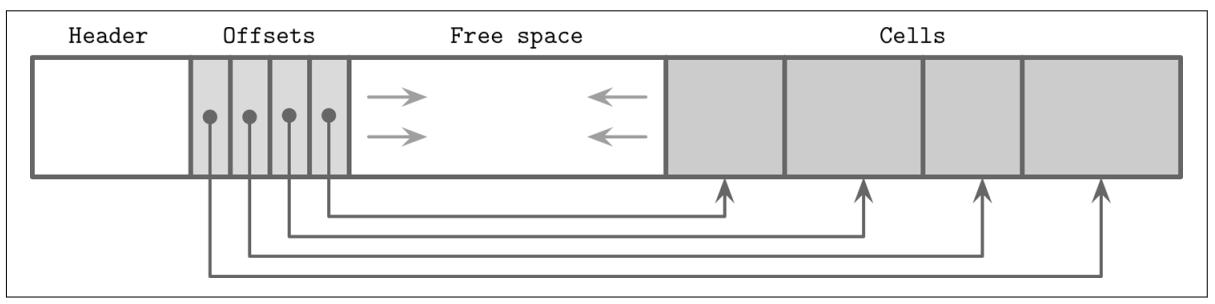
Для организации ячеек в страницы, мы можем пользоваться той техникой Перекидных страниц, которую мы обсудили в разделе Перекидные страницы. Мы добавляем ячейки в правую сторону такой страницы (со стороны её конца) и сохраняем смещения/ указатели в левой стороне данной страницы, как это показано на Рисунке 3-6.
Ключи можно вставлять в не упорядоченно, а порядок их логической сортировки удерживается через сортировку указателей смещений ячеек в следовании ключей. Такое решение позволяет добавлять ячейки в конец данной страницы с минимальными усилиями, в то время как ячейки не приходится перемещать в процессе операций вставки, обновления или удаления.
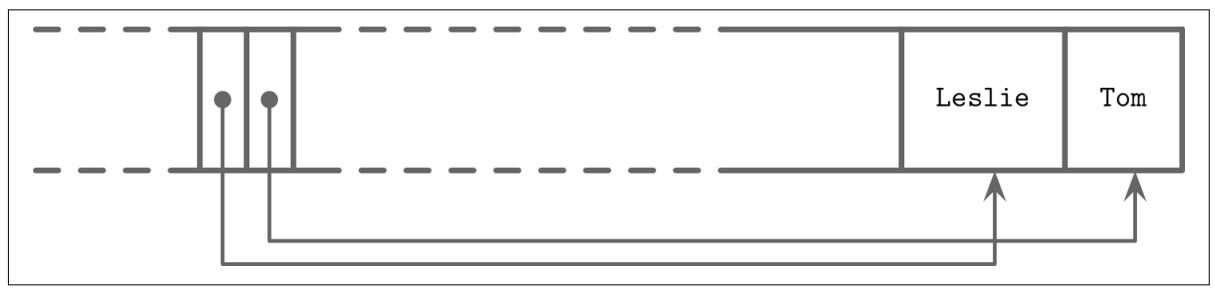
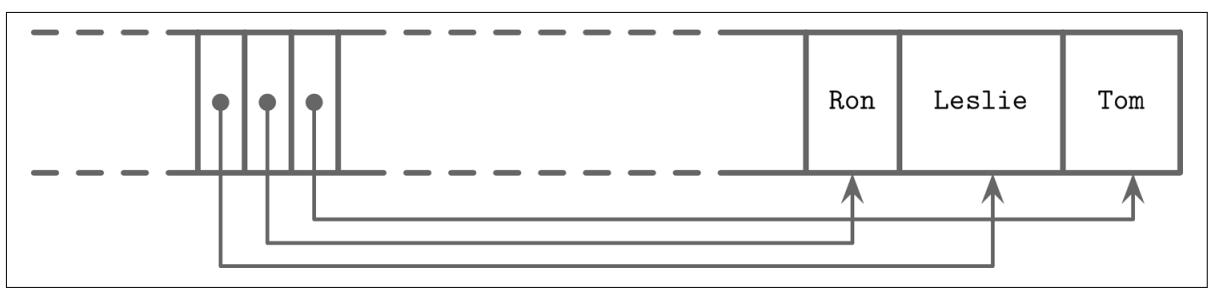
Давайте рассмотрим некий пример страницы, содержащей имена. В данную страницу добавляются два имени, причём порядок их вставки таков: Tom и Leslie. Как вы можете видеть на Рисунке 3-7, их логический порядок (в данном случае алфавитный), не соответствует порядку вставки (тому порядку, в котором они вставлялись в конец этой страницы). Ячейки располагаются в порядке вставки, но смещения сортируются повторно делая для наз возможным двоичный поиск.
Теперь мы бы хотели добавить в эту страницу ещё одно имя: Ron. Новые данные добавляются к верхней границе свободного пространства этой страницы, однако смещениям ячеек приходится предохранять установленный лексикографический порядок ключей: Leslie, Ron, Tom. Для этого нам приходится повторно упорядочить смещения ячеек: указатели после такой точки вставки сдвигаются вправо для предоставления пространства под ячейку Ron, как это можно видеть на Рисунке 3-8.
Удаление некого элемента из определённой страницы не удаляет реальную ячейку и не сдвигает прочие ячейки для перераспределения высвобождающегося свободного пространства. Вместо этого ячейка может быть помечена как удалённая, а расположенный в памяти список доступности может быть обновлён этим значением освобождаемой памяти с освобождением данного значения указателя. Такой список доступности хранит смещения освобождённых сегментов и их размеров. При вставке новой ячейки мы вначале проверяем список доступности для обнаружения того имеется ли некий сегмент, в котором она могла бы уместиться. На Рисунке 3-9 вы можете видеть некий образец фрагментированной памяти с доступными сегментами.
Рисунок 3-9
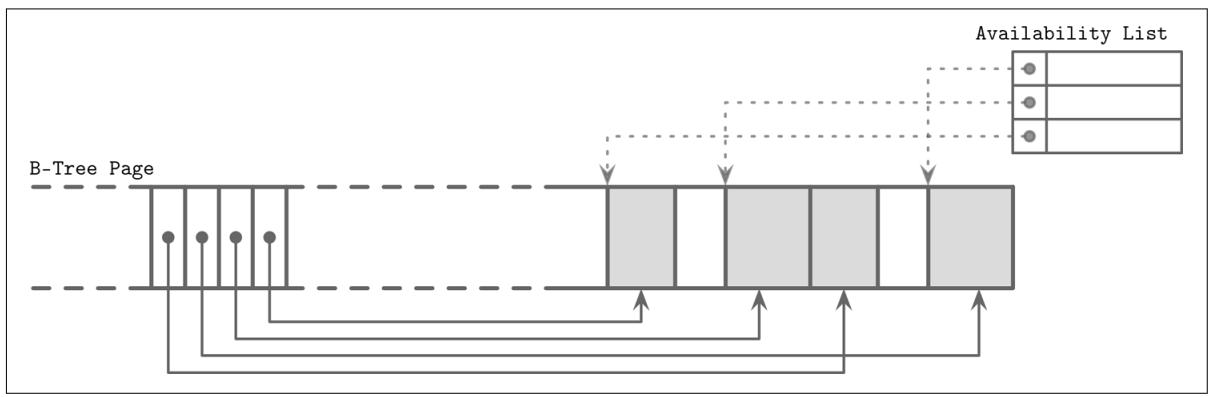
Фрагментированная страница и список доступности. Занятые страницы показаны серым. Линии с точуой представляют собой указатели на незанятые области из имеющегося списка доступности.
SQLite именует не занятые сегменты свободными блоками (freeblocks) и хранит некий указатель на самый первый свободный блок в заголовке самой страницы. Кроме того, он хранит общее число доступных байт внутри самой страницы для быстрой проверки будем ли мы иметь возможность размещать некий новый элемент в этой странице после её дефрагментации.
Подгонка вычисляется на основании определённой стратегии:
- Подгоняется первый
Это может вызывать несколько большие накладные расходы, так как остающееся после повторного использования пространство применения самого первого подходящего сегмента может оказываться слишком маленьким чтобы подходить под какие бы то ни было прочие ячейки, а потому они будут на практике тратиться впустую.
- Укладывается лучше всего подходящий
Для подходящего наилучшим образом мы пытаемся отыскать некий сегмент, для которого вставка оставляет наименьший остаток.
Когда мы не можем найти некого сегмента с последовательно идущими байтами для размещения своей новой ячейки, но имеется достаточно доступных байт, живые ячейки считываются и перезаписываются, выполняя дефрагментацию имеющейся страницы и возвращённого пространства под новые записи. Когда остающегося свободным пространства недостаточно даже после его дефрагментации, нам приходится создавать некую страницу переполнения (см. раздел Страницы переполнения).
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Для улучшения локальности (в особенности когда ключи имеют малый размер), некоторые реализации хранят ключи и значения по отдельности на имеющемся терминальном уровне. Совместное удержание ключей способно улучшать имеющуюся локальность в процессе выполняемого поиска. После того как искомый ключ найден, его значение может быть обнаружено в ячейке значения с соответствующим индексом. Для ключей с переменной длиной это потребует от нас вычисления и сохранения некого дополнительного указателя на значение ячейки. |
Чтобы суммировать, для упрощения схемы B- дерева мы предполагаем что каждый узел занимает некую отдельную страницу. Страница состоит из заголовка с фиксированным размером, блок указателей ячеек и ячейки. Ячейки содержат ключи и указатели на те страницы, которые отвечают за дочерние узлы или связанные записи данных. B- деревья используют простую иерархию указателей: указатели страниц задают место своих дочерних узлов в имеющемся файле дерева, а смещения ячеек на расположение ячеек внутри такой страницы.
Системы баз данных непрерывно эволюционируют и разработчики работают над добавлением функциональных возможностей, а также исправлением ошибок и проблем с производительностью. В результате этого может изменяться и двоичный формат файла. В большинстве случаев любой версии механизма хранения приходится поддерживать более одного формата сериализации (то есть текущий и один или более унаследованных форматов для обратной совместимости). Для такого сопровождения нам приходится иметь возможность определять с какой именно версией файла мы имеем дело.
Это можно выполнять различными способами. Например, Apache Cassandra применяет в названиях файлов префиксы
используемых версий. Таким образом, вы можете сказать какая версия у данного файла даже не открывая его. Когда
версия 4.0, некое название файла имеет префикс названия файла na, скажем,
na-1-big-Data.db. Более старые файлы имеют иные префиксы: записанные с версией
3.0 файлы имеют префикс ma.
В качестве альтернативы, номер версии может храниться в неком отдельном файле. Например, PostgreSQL хранит номера версий в своём файле PG_VERSION.
Номер версии также может храниться непосредственно в самом заголовке файла индексов. В таком случае часть такого заголовка (или даже заголовок целиком) приходится кодировать в неком формате, который не меняется между версиями. После отыскания того с какой версией кодируется данный файл, мы можем создать некий особый для версии считыватель чтобы интерпретировать его содержимое. Некие форматы идентифицируют номер версии при помощи магических чисел, которые мы обсуждаем подробнее в разделе Магические числа.
Файлы на диске могут разрушаться или искажаться за счёт ошибок программного обеспечения и отказов оборудования. Для предварительного выявления таких проблем и чтобы избегать распространения нарушенных данных в прочие системы или даже узлы мы можем применять контрольные суммы и циклические проверки избыточности (CRC, cyclic redundancy checks).
Некоторые источники делают различие между криптографическими и не криптографическими хэширующими функциями, CRC и контрольными суммами. То что в них во всех выступает общим местом, так это то, что они сокращают большой кусок данных до некого небольшого числа, однако их варианты применения, цели и предоставляемые гарантии различны.
Контрольные суммы предоставляют самый слабый вид гарантии и не способны выявлять нарушения во множестве бит. Обычно
они вычисляются при помощи XOR с частичными проверками или суммированиями
[KOOPMAN15].
CRC способны способствовать выявлению ошибок разрушений (например, когда получены нарушения во множестве) [STONE98]. Критически важно выявлять ошибки во множестве бит, так как значительное процентное соотношение отказов в сетевых средах взаимодействия и устройствах хранения выявляется именно так.
![[Предостережение]](/common/images/admon/warning.png) | Предостережение |
|---|---|
|
Для проверки того были подделаны данные или нет не должны использоваться нельзя применять не криптографические хэш- значения и CRC. Для такой цели вы всегда обязаны применять надёжные криптографические хэши, разработанные именно для обеспечения безопасности. Основная цель CRC состоит в том, чтобы убедиться что в данных отсутствуют непреднамеренные и случайные изменения. Эти алгоритмы не предназначены для противодействия атакам и умышленным изменениям данных. |
Перед записью своих данных на диск, мы вычисляем их контрольные суммы и записываем их вместе с этими данными. При обратном считывании мы вычисляем их контрольную сумму снова и сопоставляем её с записанным значением. Если имеется некое расхождение в контрольных суммах, мы знаем что произошло разрушение и нам не следует пользоваться считанными данными.
Поскольку вычисления некой контрольной суммы всего файла часто не является практичным, и скорее всего придётся считывать его содержимое целиком при каждом к нему обращений, обычно вычисляются контрольные суммы страниц и помещаются в заголовок самой страницы. Тем самым контрольные суммы могут быть более прочными (ибо выполняются для некого небольшого подмножества данных), а файл целиком не будет разрушен когда нарушение содержится в единственной странице.
В этой главе мы изучили двоичную организацию данных: как выполнять сериализацию примитивных типов данных, составлять их в ячейки, строить перекидные страницы ячеек и выполнять навигацию в этих структурах.
Мы изучили как обрабатывать типы данных переменной длины, такие как строки, последовательности байт и массивы, а также составлять особые ячейки, которые поддерживают некий размер содержащихся в них данных.
Мы обсудили формат перекидных страниц, который позволяет нам ссылаться на индивидуальные ячейки внутри рассматриваемой страницы по идентификатору ячейки, сохранять данные в порядке их вставки и поддерживать необходимый порядок ключей сортировкой смещений ячеек.
Эти принципы могут применяться для составления двоичных форматов дисковых структур и сетевых протоколов.
![[Замечание]](/common/images/admon/note.png) | Последующее чтение |
|---|---|
|
Если вы желаете узнать больше относительно упоминавшихся в этой главе понятий, вы можете ссылаться на следующие источники:
|