Глава 7. Хранилище структурированного журнала
Содержание
"Бухгалтеры не пользуются ластиком, либо кончают свои дни за решёткой"
- Пэт Хелланд
Когда бухгалтерам приходится изменять имеющуюся запись, вместо того чтобы стирать ластиком уже имеющееся значение, они создают некую новую запись с исправлением. При публикации соответствующего квартального отчёта он может содержать незначительные изменения, исправления и корректировку результатов их предыдущего квартала. Для вывода самой нижней строки вам придётся пройти по всем записям и вычислять подитоги [HELLAND15].
Аналогично, неизменные структуры хранения не допускают изменений в своих имеющихся файлах: таблицы записываются один раз и никогда не изменяются снова. Вместо этого в конец соответствующего нового файла добавляются новые записи, а чтобы обнаружить окончательный результат (или заключить об его отсутствии), записи приходится восстанавливать из множества файлов. В противоположность этому, изменяемые структуры хранения модифицируют записи на диски по месту хранения.
Неизменные структуры данных часто используются в функциональных языках программирования и становятся всё более распространёнными благодаря их свойствам безопасности: будучи когда- то созданной, некая неизменная структура не изменяется, ко всем ссылкам на неё можно получать одновременный доступ, а её целостность обеспечивается тем фактом, что она не может подвергаться изменениям.
На неком верхнем уровне существует строгое отличие между тем как данные трактуются внутри некого хранилища и вне его. Внутренне, неизменные файлы могут удерживать множество копий, причём более поздние переписывают старые, в то время как изменяемые файлы обычно вместо этого хранят лишь самую позднюю. При доступе к ним, неизменные файлы обрабатываются, причём согласовываются избыточные копии и самая последняя возвращается запрашивающему её клиенту.
Как это делают и прочие книги и статьи по данному предмету, мы применяем B- деревья в качестве обычного примера изменяемой структуры и Деревья слияния структурированного журнала (Log-Structured Merge Trees, LSM- деревья) как некий образец неизменной структуры. Неизменные LSM- деревья применяют хранилище с добавлением исколючительно в конец и согласование слияний, а B- деревья размещают записи данных на диске и обновляют страницы по их первоначальным смещениям в своём файле.
Структуры хранения с обновлением по месту размещения оптимальны для производительности чтения [GRAEFE04]: после определения их места на диске, данная запись может быть возвращена запросившему её клиенту. Это достигается за счёт затрат в производительности записи: для обновления имеющейся записи данных по её месту, вначале требуется её найти. С другой стороны, хранилище с исключительной записью в конец оптимизировано под производительность записи. Операциям записи не приходится отыскивать место на диске для его перезаписи. Тем не менее, это делается за счёт затрат на чтения, которым приходится выполнять выборку множества версий записей данных и согласовывать их.
До сих пор мы в основном обсуждали изменяемые структуры хранения. Мы затронули такую тему неизменности при обсуждении B- деревьев копирования- записью (см. раздел Копирование записью), FD- деревья (см. раздел FD- деревья) и Bw- деревья (см. раздел Bw- деревья). Однако имеются и прочие способы реализации неизменных структур.
По причине своей структуры и подхода к построению, принятого в изменяемых B- деревьях, большинство операций ввода/ вывода в процессе чтения, записи и сопровождения являются случайными. Всякой операции записи вначале требуется определить некую страницу, которая содержит запись данных и лишь затем может изменять её. B- деревья требуют расщепления и слияния узлов, которые перемещают уже сохранённые записи. По истечению некоторого промежутка времени, страницы B- дерева могут потребовать работ по сопровождению. Страницы фиксированы в размере и некоторое пространство зарезервировано под последующие записи. Другая проблема состоит в том, что даже когда изменяется лишь одна ячейка в определённой странице, приходится переписывать всю страницу целиком.
Существуют альтернативные подходы, которые могут помочь в снижении этих проблем, делая некоторые из необходимых операций ввода/ вывода последовательными и избегая перезаписывания страниц в процессе их изменения. Один из таких подходов состоит в применении неизменных структур. В данной главе мы сосредоточимся на LSM деревьях: как они строятся, какими свойствами обладают и чем они отличаются от B- деревьев.
При обсуждении B- деревьев мы заключили что накладные расходы пространства и прирост записей могут улучшаться за счёт буферизации. В целом существуют два способа буферизации, которые можно применять к различным структурам хранения: затягивание записи на расположенные на диске страницы (что мы наблюдали для FD- деревьев и для WiredTiger) или превращать операции записи в последовательные.
Одно из наиболее популярных не изменяемых дисковых структур хранения, LSM дерео, для достижения последовательных записей пользуется буферизацией и хранилищем с исключительным добавлением в конец. Такое LSM дерево выступает неким вариантом располагающейся на диске структуры, аналогичной B- дереву, в которой узлы заняты целиком, являясь оптимизированными для последовательного дискового доступа. Это понятие впервые было ведено в статье Патрика О'Нийла и Эварда Ченга [ONEIL96]. Деревья слияния структурированных журналов (Log-structured merge trees) получили своё название от файлсистем со структурированными журналами, которые записывают на диск все изменения в неком подобном журналу файле[ROSENBLUM92].
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
LSM деревья записывают неизменяемые файлы и сливают их со временем воедино. Эти файлы обычно содержат некую собственную индексацию для содействия читателям в эффективном определении местоположения данных. Даже хотя LSM деревья часто представляются в виде некой альтернативы B- дервьям, распространённым является использование B- деревьев в качестве собственной внутренней структуры индексации неких неизменяемых файлов LSM деревьев. |
Слово "слияние" (merge) в LSM дереве указывает, что по причине своей неизменности, содержимое деревьев сливается при помощи некого подхода, аналогичного сортировке слиянием. Это происходит в процессе сопровождения для высвобождения пространства, занимаемого имеющимися избыточными копиями, а также в процессе считываний перед тес как содержимое может быть возвращено своему пользователю.
LSM деревья откладывают записи файла данных и буферируют изменения в расположенной в памяти таблице. Эти изменения затем распространяются записью их содержимого прочь в неизменяемые дисковые файлы. Все записи данных остаются доступными в памяти пока такие файлы не окажутся целиком сохранёнными.
Сохранение файлов данных неизменными способствует последовательным записям: данные записываются на диск единым проходом и файлы являются дописываемыми исключительно в конец. Изменяемые структуры могут предварительно выделять блоки в неком отдельном проходе (например, индексно- последовательный метод доступа - ISAM, indexed sequential access method [RAMAKRISHNAN03] [LARSON81]), однако последовательным доступам всё ещё требуются произвольные чтения и записи. неизменные структуры позволяют нам располагать записи данных последовательно во избежание фрагментации. Кроме того, неизменные файлы обладают более высокой плотностью: мы не резервируем никакое дополнительное пространство для записей данных, которые мы намерены записывать в последствии, либо для ситуаций, при которых обновления записей потребуют большего пространства нежели изначально записанные.
Так как файлы неизменяемые, операции вставки, обновления и удаления не требуют определения места записей данных на диске, что значительно улучшает производительность записи и пропускную способность. Вместо этого допускается дублирование содержимого, а конфликты разрешаются в процессе самого времени считывания. LSM деревья в особенности полезны для приложений, в которых записи гораздо более распространены чем считывания, что часто имеет место в современных системах с интенсивными данными, предоставляя постоянно увеличивающиеся объёмы данных и скорости их получения.
В соответствии с архитектурой, чтения и записи не пересекаются, поэтому данные на диске могут считываться и записываться без блокирования сегментов,то значительно упрощает одновременный доступ. В противоположность этому, изменяемые структуры пользуются иерархическими блокировками и защёлками (дополнительные сведения о блокировках и защёлках вы можете найти в разделе Управление одновременностью) для обеспечения целостности дисковых структур данных и допуска множество одновременных читателей, но требуя исключительного обладания поддеревом для писателей. Механизмы хранения на основе LSM применяют линеаризуемые в памяти представления данных и индексных файлов и им приходится лишь ограждать одновременные доступ к своим структурам для управления ими.
И B- деревья и LSM деревья для оптимизации производительности требуют некого ухода, однако по различным причинам. Так как общее число выделяемых файлов неуклонно растёт, LSM деревьям приходится сливать и перезаписывать файлы чтобы быть уверенным что в процессе чтения доступ осуществляется к наименьшему возможному числу файлов, ибо запрашиваемые записи данных могут быть разбросаны по множеству файлов. С другой стороны, изменяемые файлы могут частично или целиком перезаписываться для снижения фрагментирования и возврата пространства, занимаемого обновлениями или удалёнными записями. Конечно, точный объём выполняемых процессом уборки работ в сильной степени зависит от особенностей конкретной реализации.
Мы начинаем с упорядоченных LSM деревьев [ONEIL96], в которых поля хранят сортированные записи данных. Позднее, в разделе Неупорядоченное хранилище LSM, мы также обсудим структуры, которые позволяют хранить данные в порядке их вставки, что имеет некие очевидные преимущества по пути их записи.
Как мы только что обсуждали, LSM деревья состоят из компонентов меньшего размера, располагающихся в памяти и на диске. Для записи неизменного содержимого н диск, вначале необходимо их буферировать в памяти и сортировать их содержимое.
Расположенный в памяти компонент (часто именуемый memtable, таблицей в памяти) изменяемый: он буферирует записи данных и служат целью операций чтения и записи. Содержимое таблицы в памяти сохраняется на диск пр достижении его размером настроенного порогового значения. Обновления таблицы в памяти не влечёт за собой дискового доступа и не требует связанных с вводом/ выводом затрат. Для обеспечения долговечности записей данных отдельного файла журнала упреждающей записи, аналогичного обсуждавшемуся нами в разделе Восстановление. Записи данных добавляются в конец этого журнала и фиксируются в памяти перед отправкой подтверждения своему клиенту.
Буферизация выполняется в памяти: все операции чтения и записи применяются к расположенной в памяти таблице, которая поддерживает некую сортированную структуру данных, делая возможным одновременный доступ, как правило, в виде расположенного в памяти сортированного дерева, либо любой структуры данных, которая способна выдавать подобные показатели производительности.
Располагающиеся на диске компоненты строятся путём сброса (flushing) буферированного в памяти содержимого на диск. Расположенные на диске компоненты используются исключительно для чтения: буферированное содержимое сохраняется и файлы никогда не изменяются. Это позволяет нам мыслить в терминах простых операций: записей в некую таблицу в памяти и чтения с диска и из таблицы в памяти, слияний и удалений файлов.
На протяжении данной главы мы будем применять слово таблица в качестве сокращения для располагаемой на диске таблицы. Поскольку мы обсуждаем семантику механизма хранения, этот термин не имеет двоякого толкования с понятием таблицы в более широком смысле систем управления базами данных.
Двухкомпонентные LSM деревья
Мы различаем двухкомпонентные и многокомпонентные LSM деревья. Двухкомпонентные LSM деревья имеют лишь один дисковый компонент, составляемый из неизменяемых сегментов. Дисковый компонент организован как B- дерево со 100% занятостью узлов и доступными только для чтения страницами.
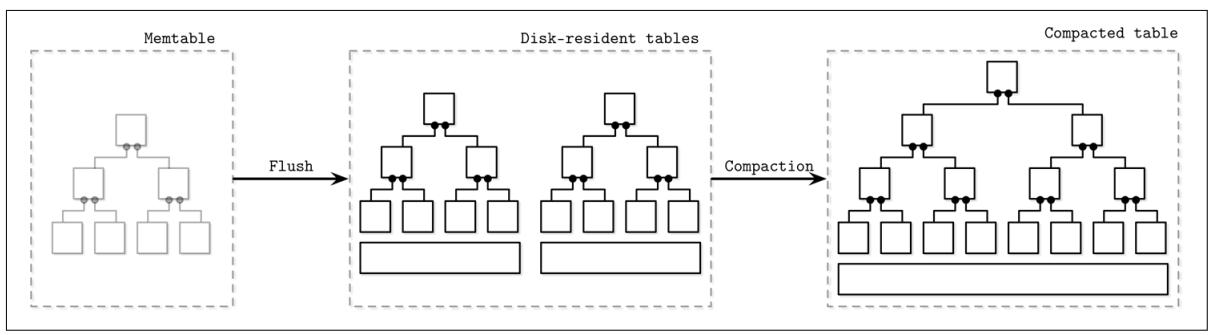
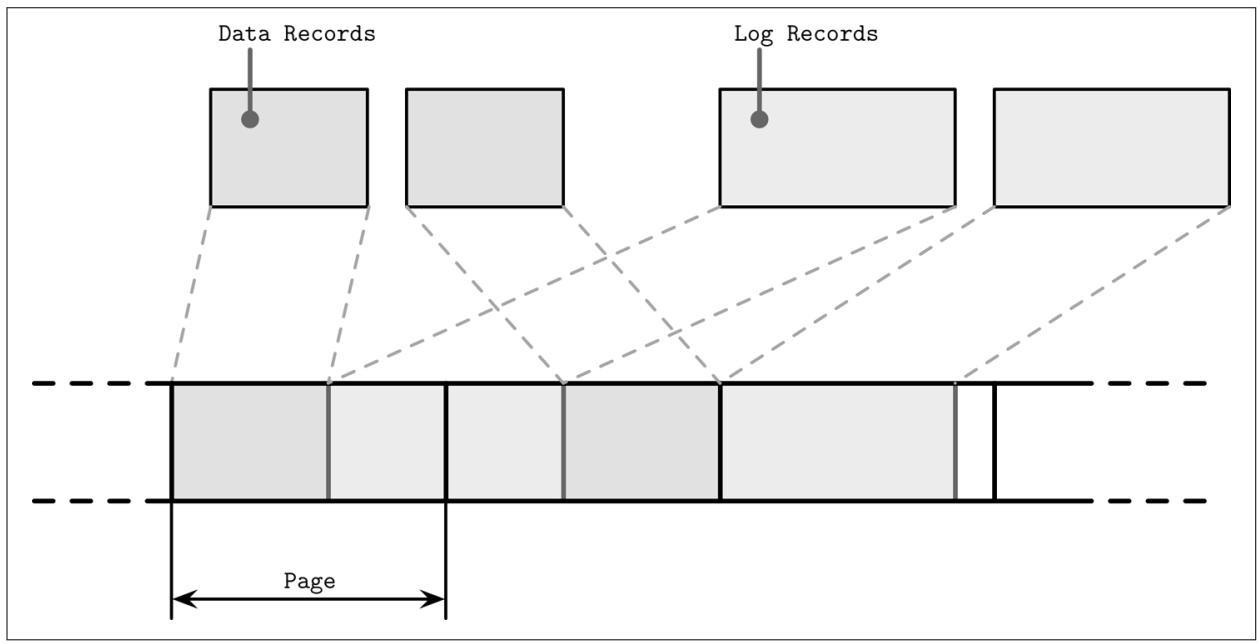
Расположенное в памяти содержимое дерева сбрасывается на диск частями. В процессе сброса, для каждого сбрасываемого поддерева из памяти мы определяем соответствующее поддерево на диске и записываем содержимое слияния располагаемого в памяти сегмента с дисковым поддеревом в некий новый сегмент на диске Рисунок 7-1 отображает деревья в памяти и на диске перед слиянием.
Рисунок 7-1
Двухкомпонентное LSM дерево перед сбросом. Сбрасываемые сегменты, расположенные в памяти и на диске показаны серым.
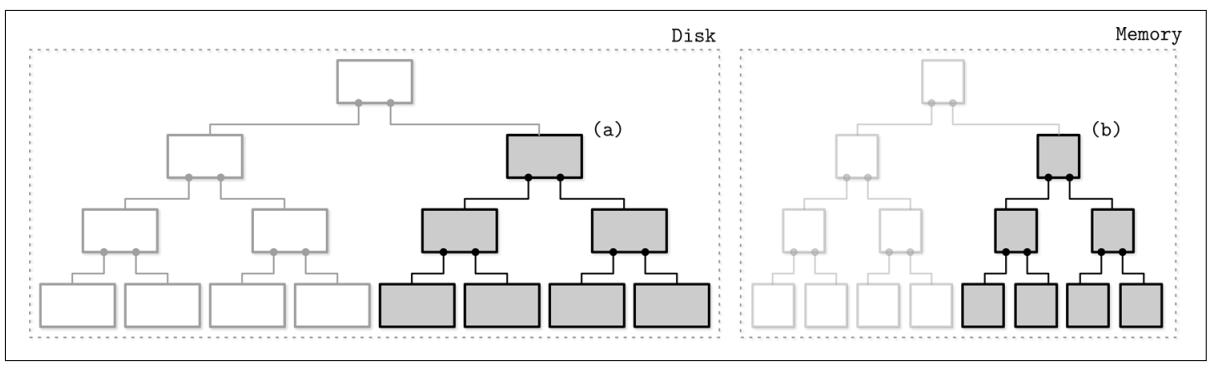
После сброса этого поддерева, заменяемые поддеревья из памяти и с диска отбрасываются и заменяются результатом их слияния, которые получают адреса из предшествующих разделов своего расположенного на диске дерева. Рисунок 7-2 отображает результат процесса слияния, который уже записан в новом месте на диске и присоединён к остальному дереву.
Рисунок 7-2
Двухкомпонентное LSM дерево после сброса. Слитое содержимое показано серым. Показанные пунтиром блоки отображают отброшенные дисковые сегменты.
Слияние может быть реализовано продвижением в строгом соответствии итераторов чтения соответствующих располагающихся на диске терминальных узлов содержимого имеющегося в памяти дерева. Поскольку оба источника отсортированы, для того чтобы произвести некий сортированный результат слияния вам требуется знать сами текущие значения обоих итераторов в процессе каждого шага данного процесса слияния.
Такой подход является логичным расширением и продолжением нашего обсуждения неизменяемых B- деревьев. Деревья копирования записью (см. раздел Копирование записью) применяют структуру B- дерева, но их узлы не полностью заняты и они требуют копирования страниц по всему пути от корня к листьям и создания некой параллельной структуры. В данном случае мы делаем нечто аналогичное, но поскольку мы буферируем записи в памяти, мы возмещаем основную стоимость обновления своего расположенного на диске дерева.
При реализации слияний и сброса поддеревьев, нам приходится гарантировать три момента:
-
Каак только стартует процес сброса, всем новым записям приходится переходить в новую таблицу в памяти.
-
На протяжении сброса данного поддерева и расположенное на диске и сбрасываемое из памяти поддеревья должны оставаться доступными на чтение.
-
После выполнения сброса, публикация слитого содержимого и отбрасывания не подвергшегося слиянию располагаемого на диске и в памяти содержимого должны выполняться атомарно.
Даже несмотря на то, что двухкомпонентные LSM деревья могут быть полезными для поддержки индексных файлов, на момент написания книги автору не известно ни об одной реализации. Это можно объяснить свойствами прироста записей для такого подхода: слияния относительно частые, поскольку они включаются сбросами таблиц в памяти.
Многокомпонентные LSM деревья
Давайте рассмотрим некую альтернативную архитектуру, многокомпонентные LSM деревья, которые имеют более одной расположенной на диске структуры. В этом случае всё содержимое таблицы в памяти сбрасывается за один прогон.
Быстро становится очевидным, что после множества сбросов мы в конечном итоге приходим к множеству расположенных на диске таблиц и со временем их общее число будет только расти. Так как нам не всегда известно какие таблицы содержат требуемые записи данных, нам может потребоваться доступ ко множеству файлов для выявления искомых данных.
Наличие потребности чтения множества источников вместо всего одного может быть достаточно затратным. Для смягчения этой проблемы и удержания числа таблиц минимальным, периодически включается процесс слияния, носящий название упаковки (compaction, см. раздел Сопровождение в деревьях LSM). Упаковка выхватывает некоторые таблицы, считывает их содержимое, сливает его и записывает результаты слияния в новый комбинированный файл. Одновременно с появлением таких новых таблиц слияния отвергаются старые таблицы.
Рисунок 7-3 отображает жизненный цикл данных многокомпонентного LSM дерева. Когда оно становится слишком большим,его содержимое сбрасывается на диск для создания располагающихся на диске таблиц. Затем множество таблиц сливаются воедино для создания таблиц большего размера.
Остальная часть данной главы посвящена многокомпонентным LSM деревьям, болкам построения и процессу их сопровождения.
Таблицы в памяти
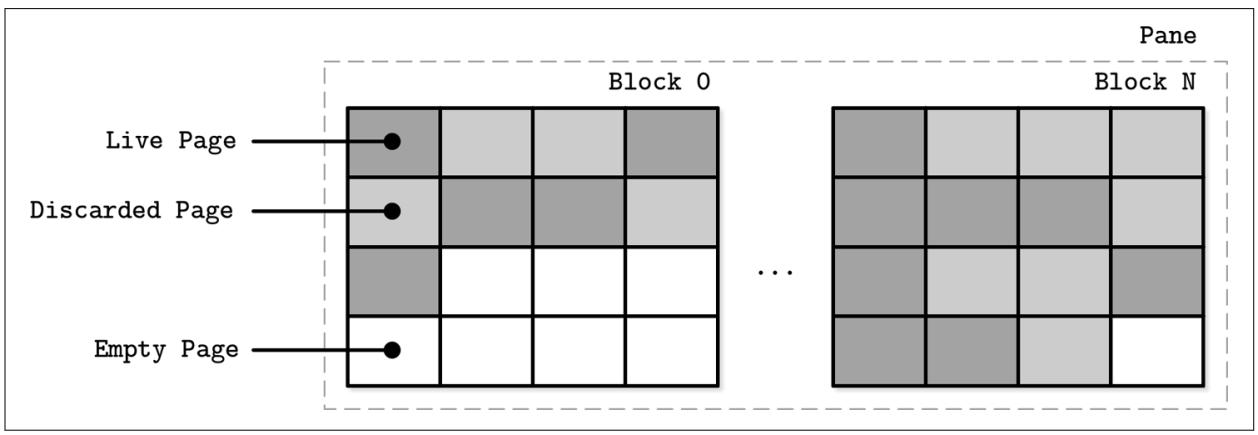
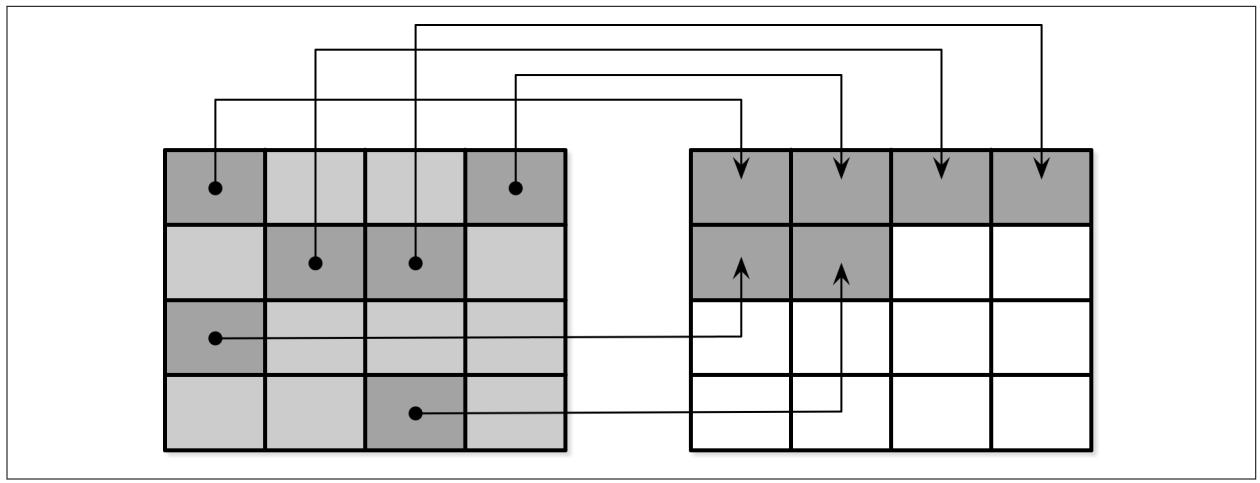
Сбросы таблиц в памяти (memtables) могут включаться периодически, либо применять некий размер порогового значения. Перед тем как сбросить их, такая таблица в памяти должна быть переключена: выделяется некая новая таблица в памяти, и именно она становится целью для новых записей, в то время как старая перемещается в состояние сбрасываемой. Эти два шага должны выполняться атомарно. Наша сбрасываемая таблица остаётся доступной для чтений пока её содержимое не будет полностью сброшено. После этого наша старая таблица в памяти отвергается в пользу новой записанной на диск таблицы, которая и становится доступной для чтения.
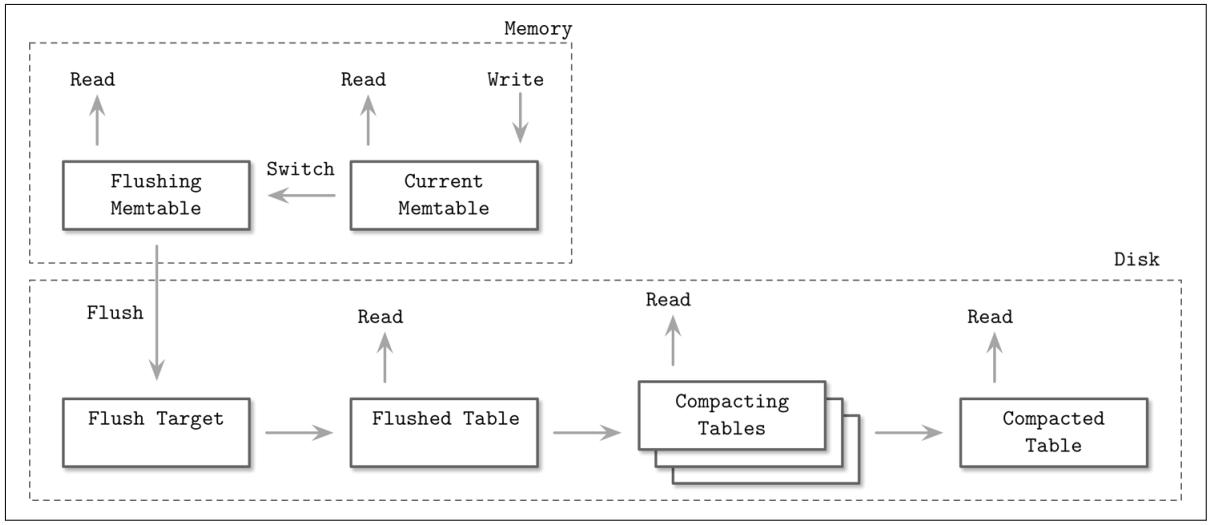
На Рисунке 7-4 вы можете видеть компоненты определённого LSM дерева, взаимосвязи между ними и операции, которые совершают переход между ними:
- Текущая таблица в памяти (Current memtable)
Получает записи и обслуживает чтения.
- Сбрасываемая таблица в памяти (Flushing memtable)
Доступна для чтения.
- Цель сброса на диске (On-disk flush target)
Не принимает участия в операциях чтения, ибо её содержимое не завершено.
- Сброшенные таблицы (Flushed tables)
Доступны для чтения как только отвергнута соответствующая сбрасываемая таблица в памяти.
- Упаковываемые таблицы (Compacting tables)
Сливаемые в данный момент и располагаемые на диске таблицы.
- Упакованные таблицы (Compacted tables)
Созданные из сброшенных проих упаковываемых таблицы.
Данные уже отсортированы в памяти, поэтому располагаемые на диске таблицы могут создаваться последовательной записью на диск расположенного в памяти содержимого.
До тех пор пока соответствующая таблица в памяти не сброшена целиком, в соответствующем журнале упреждающей записи хранится только располагающаяся на диске версия её содержимого. После того как содержимое таблицы в памяти окончательно сброшено на диск, этот журнал может быть усечён (trimmed) и могут быть отброшены соответствующий раздел журнала, содержащий все операции, применявшиеся к его сбрасываемой таблице.
В LSM деревьях операции вставки, обновления и удаления не требуют определения места записей данных на диске. Вместо этого избыточные записи возвращаются в процессе считывания.
Удаление записей данных из таблицы в памяти не достаточен, так как прочие располагающиеся на диске или в памяти таблицы могут содержать записи данных для того же самого ключа. Если бы мы реализовали удаления всего лишь удалением элементов из соответствующей таблицы в памяти, мы бы в конечном счёте пришли бы к той ситуации, что удаления не оказывают воздействия или были бы воскрешаемы своими предыдущими значениями.
Давайте рассмотрим некий пример. Сброшенная на диск таблица содержит запись данных v1?
связанную с ключом k1, а соответствующая таблица в памяти содержит значение
v2:
Disk Table Memtable
| k1 | v1 | | k1 | v2 |
Если мы только удалим v2 из таблицы в памяти и сбросим её, мы в действительности
воскресим v1, так как это будет единственное значение, связанное с данным ключом:
Disk Table Memtable
| k1 | v1 | ∅
По этой причине удаления необходимо записывать в явном виде. Это можно осуществлять некой специальной удаляющей записью (порой носящей название надгробия - tombstone - или некого дремлющего сертификата - dormant certificate), указывающего удаление этой записи данных со связанным с ней определённым ключом:
Disk Table Memtable
| k1 | v1 | | k1 | <tombstone> |
Наш процесс урегулирования прихватывает надгробия и отфильтровывает теневые значения.
Порой может быть полезным удаление некого последовательного диапазона ключей вместо того чтобы делать это с единственным ключом. Это может быть выполнено при помощи удалений предикатом, которое работает при помощи добавления в конец элемента удаления некого предиката, который выполняет сортировку при помощи обычных правил сортировки записей. В процессу согласования, соответствующие значению предиката записи данных пропускаются и не возвращаются своему клиенту.
Предикаты могут иметь форму DELETE FROM table WHERE key ≥ "k2" AND key <
"k4" и могут получать некий диапазон соответствия. Apache Cassandra реализует этот подход и
именует его диапазоном надгробий (range tombstones). Некий диапазон надгробий
охватывает какой- то диапазон ключей вместо единственного ключа.
При применении диапазона надгробий, по причине перекрывающихся диапазонов и границ располагаемых на диске таблиц,
разрешающие правила надлежит рассматривать аккуратно. Например, наша следующая комбинация скроет свзанные с
k2 и k3 записи данных из нашего окончательного
результата:
Disk Table 1 Disk Table 2
| k1 | v1 | | k2 | <start_tombstone_inclusive> |
| k2 | v2 | | k4 | <end_tombstone_exclusive> |
| k3 | v3 |
| k4 | v4 |
Деревья LSM состоит из множества компонентов. В процессе поиска доступ обычно осуществляется более чем к одному комоненту, а потому их содержимое должно сливаться и согласовываться прежде чем оно будет отправлено своему клиенту. Для лучшего понимания самого процесса слияния давайте рассмотрим как выполняются итерации по таблицам в процессе такого слияния и как сочетаются конфликтующие записи.
Поскольку содержимое располагаемых на диске таблиц отсортировано, мы можем применять многоканальный алгоритм слияния сортировкой. Например, у нас имеются три источника: две располагаемых на диске таблицы и одна таблица в памяти. Обычно механизм хранения применяет некий курсор или итератор для навигации по содержимому файла. Такой содержащий значение смещения самой последней потреблённой записи данных курсор может проверяться на предмет того, завершены ли итерации, и может применяться для выборки следующей записи данных.
Некая многоканальная сортировка слиянием применяет очереди с приоритетами, например,
min-heap [SEDGEWICK11],
которые содержат до N элементов (где N выступает
общим числом итераторов), которые сортируют своё содержимое и подготавливают свой следующий в строке подлежащий возврату
наименьший элемент. Головное значение каждого итератора помещается в соответствующую очередь. Некий элемент из такой головы
данной очереди устанавливается далее как минимальный из всех итераторов.
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Очередь с приоритетом является некой структурой данных, применяемой для сопровождения упорядоченной очереди элементов. В то время как обычная очередь хранит элементы в порядке их вставки (FIFO, пришедший первым, первым уходит), очередь с приоритетом выполняет повторную сортировку и тот элемент, у которого приоритет выше(или ниже) вставляется в голову данной очереди. Это в особенности полезно для итераций слияния, так как нам приходится выдавать элементы в сортированном порядке. |
Когда наименьший элемент удаляется из своей очереди, связанный с ним итератор проверяется на наличие следующего значения, которое затем помещается в эту очередь, а она повторяет сортировку для сохранения своего порядка.
Так как содержимое всех итераторов отсортировано, повторная вставка некого значения определённого итератора, который содержал предыдущее наименьшее значение из голов всех заголовков также хранит и некий инвариант, который для данной очереди, содержащий значение наименьшего элемента для всех итераторов. Всякий раз, огда некий итератор исчерпан, данный алгоритм продолжается без повторной вставки следующего головного значения этого итератора. Данный алгоритм продолжается до тех пор, пока не удовлетворятся условия запроса, либо не будут исчерпаны все итераторы.
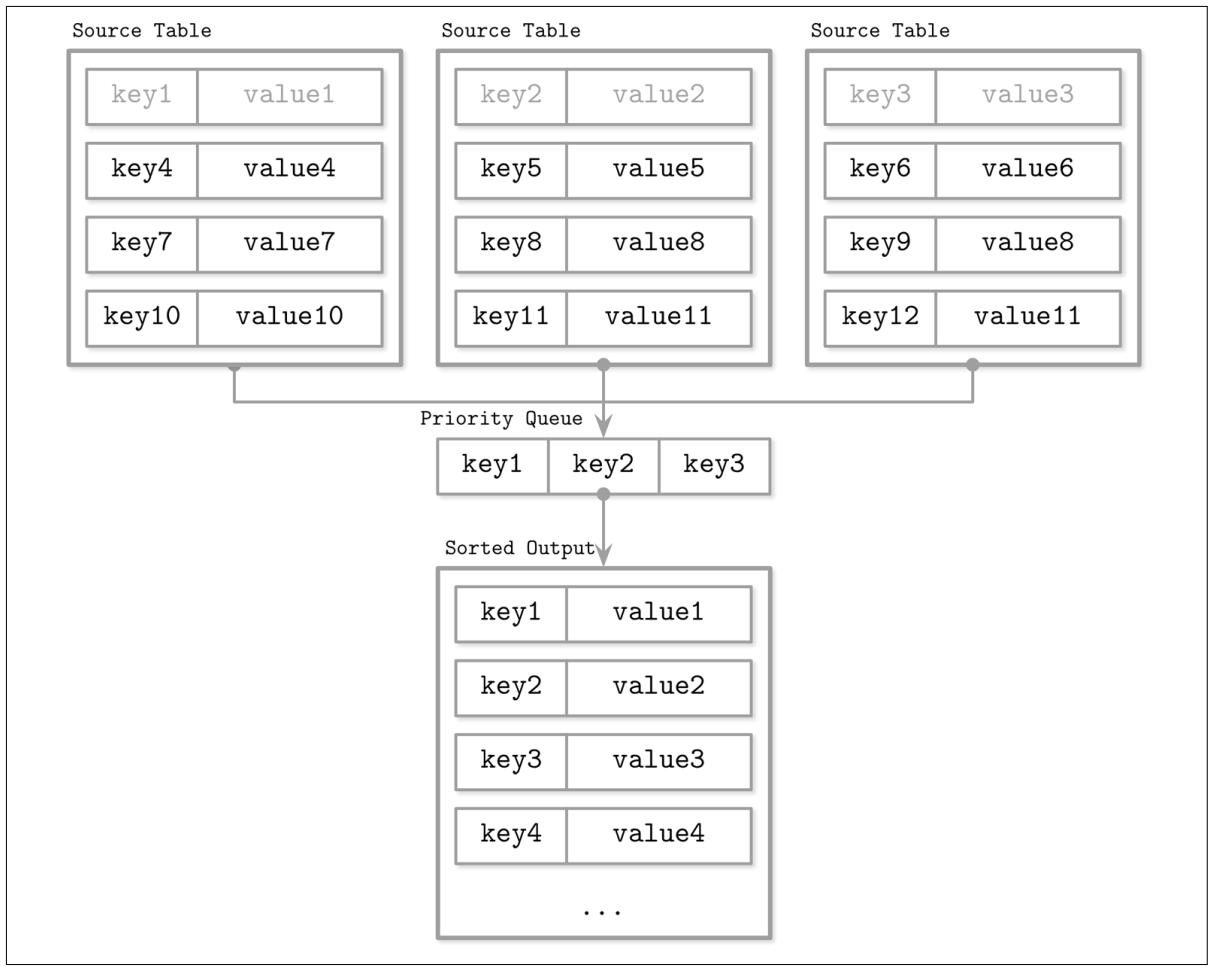
Рисунок 7-5 отображает схематическое представление только что описанного процесса слияния: головные элементы (светло серые элементы в таблицах источников) помещаются в очередь с приоритетами. Элементы из этой очереди с приоритетами возвращаются в соответствующий итератор вывода. Получаемый результат отсортирован.
Может так случиться, что мы столкнёмся с более чем одной записью данных для одного и того же ключа в процессе итераций слияния. Для своей очереди с приоритетами и инвариантов итератора нам известно, что поскольку каждый итератор содержит лишь единственную запись для ключа, а мы в конце концов получаем в своей очереди множество записей для одного и того же ключа, эти записи данных должны были поступить от различных итераторов.
Давайте пошагово пройдём по одному примеру. В качестве данных итераторов у нас имеются итераторы двух располагаемых на диске таблиц:
Iterator 1: Iterator 2:
{k2: v1} {k4: v2} {k1: v3} {k2: v4} {k3: v5}
Очередь с приоритетами заполняется головными элементами этих итераторов:
Iterator 1: Iterator 2: Priority queue:
{k4: v2} {k2: v4} {k3: v5} {k1: v3} {k2: v1}
Ключ k1 является наименьшим ключом в этой очереди и он добавляется в конец
получаемого результата. Поскольку он получен из Iterator 2, мы пополняем свою очередь
из него:
Iterator 1: Iterator 2: Priority queue: Merged Result:
{k4: v2} {k3: v5} {k2: v1} {k2: v4} {k1: v3}
Теперь у нас имеются две записи для значения ключа k2
в этой очереди. Мы можем быть уверенными, что нет никаких иных записей с этим же ключом в прочих итераторах по причине
вышеуказанных инвариантов. Записи с одним и тем же ключом сливаются и в конец очереди добавляется результат такого слияния.
Наша очередь пополняется данными из обоих итераторов:
Iterator 1: Iterator 2: Priority queue: Merged Result:
{} {} {k3: v5} {k4: v2} {k1: v3} {k2: v4}
Поскольку все итераторы теперь пустые, мы добавляем в конец своего вывода всё остающееся в очереди содержимое:
Merged Result:
{k1: v3} {k2: v4} {k3: v5} {k4: v2}
Суммарно, для создания некой комбинации итераторов следует повторять следующие шаги:
-
Первоначально заполняем свою очередь самыми первыми элементами из каждого итератора.
-
Из этой очереди получаем самый наименьший элемент (головной).
-
Заполняем свою очередь из соответствующего итератора до тех пор, пока этот итератор не будет исчерпан.
В терминах сложности, слияние итераторов это то же самое что и слияние сортированных наборов. Оно обладает накладными
расходами по памяти O(N), где N это общее
число итераторов. Сортированная коллекция заголовков итераторов препровождается с O(log N)
(в среднем) [KNUTH98].
Слияние итерациями это лишь одна из сторон того, что приходится выполнять для слияния данных из множества источников. Другой важной стороной является согласование или улаживание конфликтов для тех записей, которые связаны с одним и тем же ключом.
Различные таблицы могут содержать записи для одного и того же ключа, например, при обновлениях и удалениях, а их содержимое подлежит согласованию. Наша реализованная в предыдущем примере очередь с приоритетами должна иметь возможность допуска множества связанных с одним и тем же ключом значений и включения улаживания.
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Некая операция, которая вставляет свою запись в базу данных когда она там не присутствует и обновляет некую уже имеющуюся в противном случае имеет название upsert. В LSM деревьях операции вставки и обновления неразличимы, так как они не пытаются определять место записей данных, изначально связанных с этим ключом во всех источниках и переопределять их значения, а потому мы можем сказать, что мы по умолчанию upsert записи. |
Для согласования записей данных нам требуется понимать какая из них является предшествующей. Записи данных содержат необходимые для этого метаданные, например, временные отметки. Для установления значения порядка между ними при их поступлении из различных источников, а также поиска той, которая является самой последней, мы можем сопоставлять их временные отметки.
Скрываемые записями с более верхними временными отметками записи не возвращаются своему клиенту и не записываются в процессе уплотнения.
Аналогично изменяемым B- деревьям, LSM деревья требуют сопровождения. Сама природа этих процессов сильно подвержена воздействию тех инвариантов, которые сохраняют эти алгоритмы.
В B- деревьях процесс сопровождения собирает ячейки без ссылок и выполняет дефрагментацию страниц, высвобождая пространство, занимаемое удалёнными или перекрытыми страницами. В LSM деревьях общее число располагаемых на диске таблиц постоянно растёт, но может снижаться периодически включаемым уплотнением.
Уплотнение прихватывает множество располагаемых на диске таблиц, выполняет по всему их содержимому итерации с применением приведённых выше алгоритмов слияния и согласования и записывает получаемый результат во вновь создаваемой таблице.
Поскольку содержимое располагаемых на диске таблиц отсортировано, а также по причине самого способа слияния сортировкой, упаковка обладает некой теоретической верхней границей использования памяти, так как ему требуется удерживать в памяти лишь головные элементы итераторов. Все содержимое таблицы потребляется последовательно, а получаемые в результате слияния данные также записываются последовательно. Эти подробности могут разниться между реализациями по причине дополнительных оптимизаций.
Упаковываемые таблицы остаются доступными для чтения до тех пор, пока не завершится сам процесс упаковки, что означает, что на протяжении упаковки требуется иметь достаточно свободного пространства на диске для записи упаковываемой таблицы.
Во всякий момент времени в определённой системе может происходить множество упаковок. Тем не менее, эти одновременные упаковки обычно работают с непересекающимися наборами таблиц. Записывающая упаковку сторона может как сливать различные таблицы в одну, так и разбивать одну таблицу на множество.
![[Замечание]](/common/images/admon/note.png) | Надгробия и упаковка. |
|---|---|
|
Надгробия (tombstones) представляют некую важную часть необходимых для правильного согласования сведения, ибо прочие таблицы могут всё ещё содержать некие устаревшие записи данных, отображаемые такими надгробиями. В процессе уплотнения надгробия не отбрасываются просто так. Они представляются до тех пор, пока имеющийся механизм хранения сможет получить уверенность в том, что никакие записи данных для одного и того же ключа с меньшей временной отметкой не представлены ни в какой иной таблице. RocksDB оставляет надгробия вплоть до достижения самого нижнего уровня. Apache Cassandra оставляет надгробия вплоть до достижения периода отсрочки GC (garbage collection, сборки мусора) по причине в конечном итоге непротиворечивой природы самой базы данных, гарантирующей что прочие узлы видят эти надгробия. Сохранение надгробий во время уплотнения важно во избежание воскрешения данных. |
Упаковка по уровням
Уплотнение открывает для оптимизации множество возможностей и имеется множество различных стратегий уплотнения. Одной из часто принимаемых реализаций стратегий уплотнения имеет название упаковки по уровням. Например она применяется в RocksDB.
Выстраиваемое по уровням уплотнение разделяет размещаемые на диске таблицы по уровням. Таблицы на каждом уровне имеют целевые размеры, причём каждый уровень обладает соответствующим номером индекса (идентификатора). Что несколько нелогично, уровень с самым высоким уровнем имеет название самого нижнего уровня. Для ясности в этом разделе мы избегаем применения терминов верхний и нижний уровни и используем те же самые квалификации для индекса уровня. А именно, поскольку 2 больше чем 1, уровень 2 имеет более высокий индекс чем уровень 1. Наши термины предыдущий и следующий имеют тот же самый порядок семантики, что и индексы уровня.
Таблицы уровня 0 создаются сбросом содержимого таблиц в памяти. Таблицы из уровня 0 могут содержать перекрывающиеся диапазоны ключей. По мере того, как число таблиц уровня 0 достигает некого порогового значения, их содержимое сливается, создавая новые таблицы для уровня 1.
Диапазоны ключей для всех таблиц на уровне 1 и все уровни с более высоким индексом не перекрываются, поэтому таблицы уровня 0 должны быть разбиты на разделы в процессе уплотнения, расщепляясь по диапазонам и слиты с таблицами, содержащими соответствующие диапазоны ключей. В качестве альтернативы, уплотнение включает в себя все таблицы уровня 0 и уровня 1 и выводит разбитые по разделам таблицы уровня 1.
Уплотнения по уровням для более высоких индексов прихватывает таблицы двух соприкасающихся уровней с перекрывающимися диапазонами и производит некую новую таблицу на более высоком уровне. Рисунок 7-6 схематично отображает как наш процесс уплотнения выполняет миграцию данных между своими уровнями. Данный процесс уплотнения таблиц уровня 1 и уровня 2 произведёт некую новую таблицу на уровне 2. В зависимости от того как таблицы разбиты на части, для уплотнения могут быть захвачено множество таблиц с одного уровня.
Рисунок 7-6
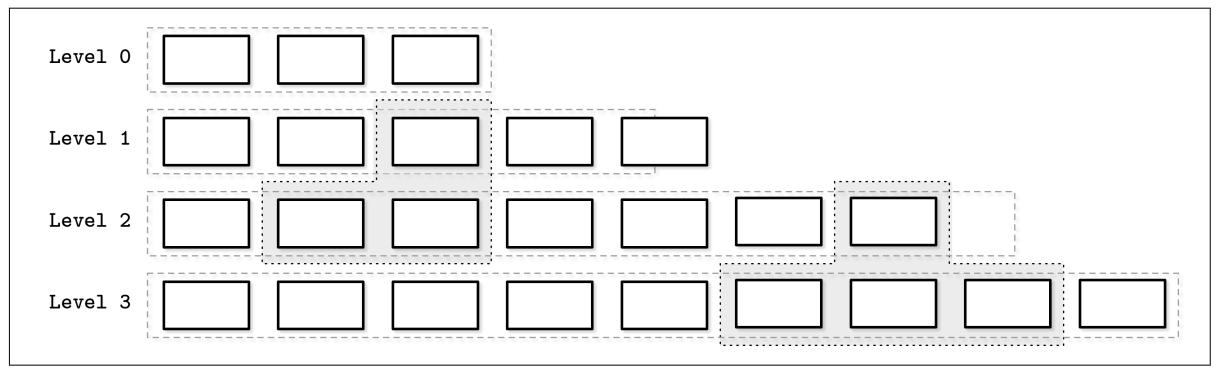
Процесс упаковки. Помеченные серым блоки в окружении пунктирных линий представляют пакуемые в данный момент таблицы. Объединяющие по уровню блоки представляют установленный предел размера цели для данного уровня. Уровень 1 превысил свой предел.
Сохранение различных диапазонов ключей в различных таблицах снижает общее число таблиц для доступа в процессе определённого чтения. Это осуществляется путём инспектирования имеющихся метаданных таблицы и отфильтровывания тех таблиц, чьи диапазоны не содержат искомого ключа.
Каждый уровень имеет некий предел для размера своих таблиц и максимального числа таблиц. Как только число таблиц на уровне 1 или любом ином уровне с более высоким индексом достигает порогового значения, таблица с данного текущего уровня сливается с таблицами следующего уровня сохраняя имеющийся диапазон перекрывающихся ключей.
Между этими уровнями размеры растут экспоненциально: таблицы на следующем уровне экспоненциально больше таблиц предыдущего уровня. Таким образом, самые свежие данные всегда находятся на самом высоком уровне с наименьшим индексом, а более старые данные постепенно мигрируют на более верхние уровни.
Стягиваемая по размеру упаковка
Другая популярная стратегия уплотнения носит наименование стягиваемой по размеру упаковки. При стягиваемом по размеру уплотнении, вместо того чтобы группировать располагаемые на диске таблицы на основании их уровня, они группируются по размеру: таблицы меньшего размера группируются с небольшими, а более крупные таблицы с большими.
Уровень 0 содержит таблицы наименьшего размера, которые либо сброшены из таблиц в памяти, либо созданы в процессе уплотнения. После того как эти таблицы уплотняются, получаемый результат слияния таблиц записывается на уровень с соответствующими размерами. Данный процесс рекурсивно повторяется, увеличивая уровни, уплотняя и продвигая таблицы большего размера на верхние уровни и опуская таблицы меньшего уровня на более нижние.
![[Предостережение]](/common/images/admon/warning.png) | Предостережение |
|---|---|
|
Одной из проблем при стягиваемом размером уплотнении является именуемая табличного голода: если уплотнённые таблицы всё ещё достаточно малы после упаковки (т.е. записи скрыты своими надгробиями и на выполняют необходимого слияния таблиц), более верхние уровни могут начинать испытывать голод уплотнения и их надгробия не будут приниматься во внимание, увеличивая стоимость чтения. В таком случае уплотнение для некого уровня должно запускаться принудительно, даже когда тот содержит достаточно таблиц. |
Существуют и иные широко реализуемые стратегии уплотнения, которые способны оптимизировать различные рабочие нагрузки. Например, Apache Cassandra также реализует некую стратегию уплотнения окна времени, которая, в частности, полезна для рабочих нагрузок временных последовательностей с записями для какого времени жизни они установлены (иными словами, элементы имеют срок истечения своего действия после заданного периода времени).
Такая стратегия уплотнения окна времени получает для рассмотрения временные отметки записи и позволяет сбрасывать файлы данных целиком, когда они содержать сведения с уже истекшим временным диапазоном без запросов от нас на упаковку и перезапись своего содержимого.
При реализации некой оптимальной стратегии уплотнения нам приходится учитывать множество моментов. Один подход возвращает занимаемое дублирующими записями пространство и снижает накладные рсходы пространства, что в результате приводит к росту записей, вызываемого непрерывными перезаписями таблиц. Его альтернатива состоит в избежании непрерывной перезаписи данных, что увеличивает рост чтений (накладные расходы согласования при чтении связанных с одним и тем же ключом записей данных), а также росту пространства (поскольку избыточные данные присутствуют большее время).
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Одной из самых больших дискуссий в сообществе баз данных состоит в том, должны ли B- деревья и LSM деревья обладать меньшим ростом записей. Чрезвычайно важно понимать сам источник роста записей в обоих случаях. В B- деревьях он поступает за счёт операций обратной записи и последовательных обновлений в одном и том же узле. В LSM деревьях рост записей вызывается миграцией данных из одного файла в другой в процессе уплотнения. Сравнение их обоих напрямую может приводить к неверным предположениям. |
Суммируя, при сохранении данных на диск неким неизменяемым образом, мы сталкиваемся с тремя задачами:
- Рост чтений
Получающийся в результате необходимости адресации ко множеству таблиц для выборки данных.
- Рост записей
Вызываемый непрерывными перезаписями необходимым процессом уплотнения.
- Рост пространства
Возникающим из- за хранения множества записей, связанных с одним и тем же ключом.
На протяжении оставшейся части главы мы будем решать каждую из них.
Одна из наиболее популярных моделей стоимости для структур хранения принимает во внимание три фактора: накладные расходы Read, Update и Memory. Она носит название предположения RUN [ATHANASSOULIS16].
Предположение RUM постулирует, что снижение двух из этих накладных расходов неминуемо приводит к изменению в худшую сторону третьего и что оптимизация может быть выполнена лишь за счёт затрат одного из трёх параметров. Мы можем сопоставлять различные механизмы хранения в терминах этих трёх параметров для понимания того, какие из них оптимизируются, а какие могут приноситься в угоду компромиссу.
Некое идеальное решение будет производить самую низкую стоимость чтения при поддержке низких накладных расходов памяти и записи, однако в действительности это недостижимо и нам представляется сделать некий компромисс.
B- деревья оптимизированы для чтения. Записи в B- дереве требуют определения места на диске для обновления множества раз соответствующей страницы на диске. Резервирование дополнительного пространства для обновлений и удалений увеличивает накладные расходы пространства.
LSM деревья не требуют определения соответствующей записи на диске в процессе записи и не резервируют дополнительное пространство для последующих записей. Всё же имеются дополнительные накладные расходы пространства, получающиеся в результате хранения избыточных записей. При некоторой конфигурации по умолчанию считывания более затратны, поскольку приходится выполнять доступ ко множеству таблиц для возврата окончательных результатов. Однако, обсуждаемые нами в этой главе оптимизации помогут снизить эту проблему.
Как мы уже видели в главах про B- деревья, и как мы увидим в этой главе, существуют способы улучшения таких характеристик применяя различные оптимизации.
Эта стоимостная модель не идеальна, так как она не принимает в расчёт прочие важные измерения, такие как задержки, шаблоны доступа накладные расходы сопровождения и относящуюся к оборудованию специфику. Для распределённых баз данных важны понятия более верхнего уровня, такие как реализация согласованности и накладные расходы репликаций, а они также не учитываются. Тем не менее, данная модель может применяться в качестве первого приближения и неким высеченным на камне правилом, ибо помогает нам понять что наш механизм хранения способен предложить.
Мы рассмотрели основную динамику LSM деревьев: как данные считываются, записываются и уплотняются. Тем не менее, существует ещё прочие моменты, которыми обычно обладают многие реализации LSM деревьев и которые неплохо обсудить: как реализуются располагаемые в памяти и на диске таблицы, как работают вторичные индексы, как снижать общее число доступов к располагаемых на дисках таблицах при чтении и, наконец, новые относящиеся к хранилищам структурированных журналов идеи.
До сих пор мы обсуждали саму иерархическую и логическую структуру LSM деревьев (что они составлены из множества располагаемых в памяти и на диске компонентов), но ещё пока не обсуждали как реализованы располагаемые на диске таблицы и как их архитектура воспроизводится совместно с остальной системой.
Располагаемые на диске таблицы часто реализуются при помощи Сортированных таблиц строк (SSTables, Sorted String Tables). Как и предполагает их название, записи данных в SSTables отсортированы и следуют в порядке их ключей. SSTables обычно состоят из двух компонентов: файлов индексов и файлов данных. Индексные файлы реализуются при помощи некой структуры, допускающей логарифмический поиск, таких как B- деревья, либо с поиском с постоянным временем, таких как хэштаблицы.
Поскольку файлы данных хранятся в порядке ключей, применение хэштаблиц для индексации не препятствует нам в реализации сканирования диапазонов, так как хэштаблица лишь выполняет доступ к местоположению самого первого ключа, а диапазон сам по себе может быть считан из самого файла данных последовательно, пока наш предикат диапазона выполняет соответствие.
Соответствующий компонент индексации содержит записи ключа и данных (смещений в соответствующем файле данных где и расположены реальные сведения). Его компонент данных состоит из объединённых пар ключ- значение. Те архитектуры ячеек и форматы записей данных, которые мы обсуждали в Главе 3,, в основном применимы и для SSTables. Основное отличие здесь состоит в том, что ячейки записываются последовательно и не могут изменяться в процессе своего жизненного цикла в этой SSTable. Поскольку наши индексные файлы содержат указатели на соответствующие записи данных, хранимые в своём файле данных, их смещения должны быть известны на момент создания самого индекса.
В процессе уплотнения файлы данных могут считываться последовательно без адресации по их значению индексного компонента, поскольку записи данных в нём уже упорядочены. Так как таблицы в процессе слияния имеют тот же самый порядок, а итерации слияния сохраняют порядок, получаемая в процессе слияния таблица также создаётся сохранением записей данных последовательно в один проход. Как только этот файл целиком записан, он рассматривается как неизменяемый и его располагаемое на диске содержимое не изменяется.
![[Замечание]](/common/images/admon/note.png) | Подключаемые к SSTable вторичные индексы |
|---|---|
|
Одной из интересных разработок в области индексации LSM деревьев являются Подключаемые к SSTable вторичные индексы (SASI, SSTable- Attached Secondary Indexes). Чтобы сделать возможной индексацию сотдержимого таблицы не только по её первичному ключу, но также и по прочим полям, структуры индексации и их жизненные циклы сочетаются с жизненным циклом SSTable и для SSTable создаётся некий индекс. При сбросе соответствующей таблицы в памяти её содержимое записывается на диск, а файлы вторичной индексации создаются совместно со значением первичного индексного ключа SSTable. Так как буферированные в памяти данные и индексы LSM дерева должны работать как для располагаемого в памяти содержимого, так и для размещаемого на диске, SASI сопровождает некую отдельную идексирующую содержимое таблиц в памяти структуру оперативной памяти. В процессе чтения первичные ключи искомых записей определяются поиском и слиянием содержимого индексов и согласовываются аналогично тому как обычно работает просмотр в LSM деревьях. Одним из основных преимуществ прихвата прицепом жизненного цикла самой SSTable является то, что индексы могут создаваться в процессе сброса или уплотнения таблиц в памяти. |
Основной источник роста чтений в LSM деревьях состоит в том, что нам приходится выполнять адресацию ко множеству располагаемых на диске таблиц для завершения самой операции чтения. это происходит по причине того, что мы не всегда знаем наперёд будут или нет располагаемые на диске таблицы содержать некую запись для искомого ключа.
Одним из способов предотвращения просмотра таблицы состоит в хранении его диапазона ключей (наименьшего и наибольшего хранимых в этой конкретной таблице ключей) в метаданных и проверять относятся ли искомые ключи к диапазону данной таблицы. Эти сведения не точны и могут лишь нам сообщить что запись данных может присутствовать в данной таблице. Для улучшения данной ситуации многие реализации, включая Apache Cassandra и RocksDB применяют структуру данных, носящую название Фильтра Блюма (Bloom filter).
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Вероятностные структуры данных обычно более эффективны в отношении пространства чем их "регулярная" противоположность. Например, чтобы проверить вхождение в множество, кардинальная мощность (определения общего числа отличающихся элементов в неком наборе) или частоты (определения того сколько раз был встречен некий определённый элемент), нам придётся хранить весь набор элементов и для обнаружения данных пройтись по всему набору данных. Вероятностные структуры позволяют нам хранить приблизительные сведения и выполнять запросы, которые несомненно дают результаты с неким элементом. Некими широко известными примерами являются Фильтры Блюма (для участия в множестве), HyperLogLog (для оценки кардинального значения) [FLAJOLET12] и Эскиз минимального подсчёта (Count-Min Sketch) [CORMODE12]. |
Фильтр Блюма, представленный Бартоном Ховардом Блюмом в 1970 [BLOOM70] является эффективной в отношении пространства вероятностной структурой данных, которая может применяться для проверки того, будет ли данный элемент участником определённого множества или нет. Они может производить ошибочные включения соответствий (сообщать, что данный элемент является участником рассматриваемого множества, когда он таковым не является), однако не способен производить ложные промахи (когда возвращается некое отрицание соответствия, данный элемент гарантировано не будет участником этого множества).
Иными словами, фильтр Блума может применяться для того чтобы сообщать нам что данный ключ может иметься в таблице, либо определённо отсутствует в этой таблице. Файлы, для которых фильтр Блюма возвращает некое отрицание соответствия, пропускаются в процессе данного запроса. Ко всем прочим файлам выполняется доступ для обнаружения того что искомая запись данных действительно присутствует. Использование связанных с располагаемыми на диске таблицами фильтров Блюма способствует значительному снижению общего числа таблиц для доступа в процессе чтения.
Фильтр Блюма использует большой массив битов и множество функций хэширования. Функции хэширования применяются к ключам
имеющихся в этой таблице записей для поиска индексаций в соответствующем массиве бит, биты для которого установлены в
1. Установленные в 1 во всех определяемых хэш
функциями позициях указывают присутствие этого ключа в данном наборе. В процессе поиска,
при проверке наличия элементов в неком фильтре Блюма, функции хэширования снова вычисляются для этого ключа и, когда определяемые
всеми хэш функциями биты равны 1, мы возвращаем
положительный результат, утверждающий что с определённой вероятностью этот элемент является участником рассматриваемого
набора. Если по крайней мере один бит равен 0, мы несомненно можем утверждать, что
этот элемент отсутствует в данном множестве.
Применяемые к разным ключам хэш функции могут возвращать одно и то же расположение бита и результат в неком
противоречии хэширования, а значение бита 1
всего лишь подразумевает, что некая хэш функция дала это положение бита для
какого- то ключа.
Вероятность ложных вхождений определяется настройкой значения размера множества бит и общего числа хэш функций: чем больше множество бит, тем меньше вероятность противоречия; аналогично, имея больше хэширующих функций, мы можем проверять больше бит и получать более точный вывод.
Большее число множества бит занимает больше памяти, а вычисляемые результаты большим числом функций хэширования могут оказывать отрицательное воздействие на производительность, поэтому нам приходится отыскивать разумную золотую середину между приемлемой вероятностью и сносными накладными расходами. Вероятность может вычисляться по ожидаемому набору множества. Поскольку LSM деревья неизменны, размер множества (общее число ключей в его таблице) известен заранее.
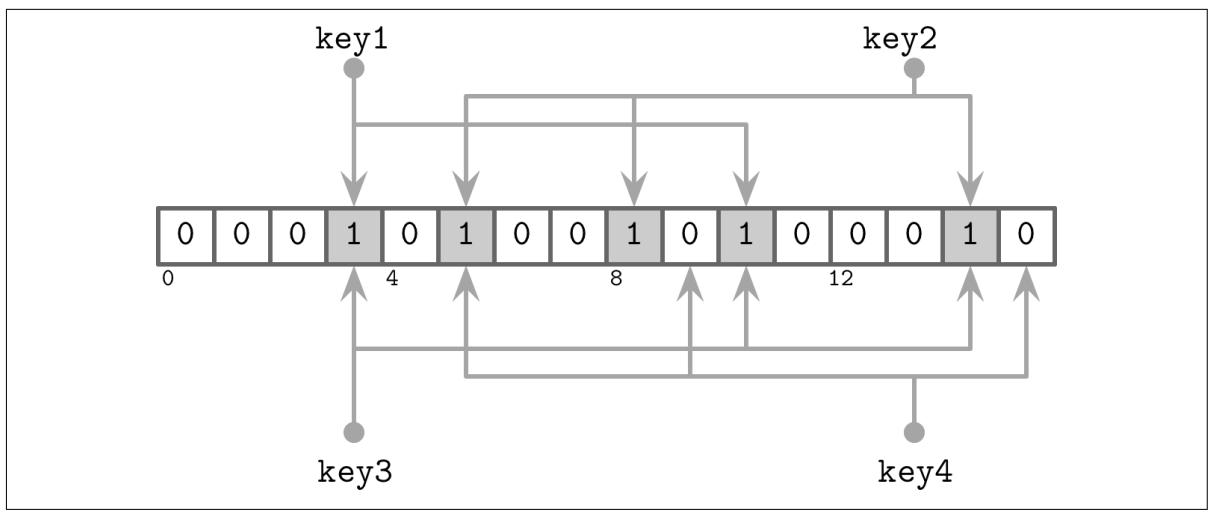
Давайте рассмотрим некий простой пример, представленный на Рисунке 7-7. У нас имеется 16- канальный массив битов и 3 хэширующих функции, которые для
key1 выдают значения 3,
5 и 10. Теперь мы устанавливаем биты в этих позициях.
Добавляется наш следующий ключ и хэш функции дают для key2 значения
5, 8 и 14,
для которых мы также устанавливаем биты.
Теперь мы пытаемся определить будет или нет key3 присутствовать в этом наборе и хэш функции
дают 3, 10 и 14.
Так как все три бита были установлены при добавлении key1 и
key2, мы получаем ситуацию, при которой наш фильтр Блюма возвращает некое
ложной вхождение: key3 здесь никогда не будет прикреплён, даже хотя установлены
все его вычисляемые биты. Однако, поскольку наш фильтр Блюма лишь утверждает что такой элемент
может присутствовать в рассматриваемой таблице, такой результат допустим.
Когда мы попытаемся выполнить поиск для key4 и получим значения
5, 9 и
15, мы обнаружим, что установлен лишь бит
5, а все прочие биты сброшены. Даже когда только один бит сброшен, мы определённо знаем,
что этот элемент никогда не был прикреплён к данному фильтру.
Существует множество различных структур данных для сохранения в памяти сортированных данных,и одним из таких, который приобретает всё большую популярность в последнее время по причине его простоты, является список пропусков (skiplist) [PUGH90b]. Широко реализуемый, список пропуска не намного сложнее чем односвязный список, а его гарантированная вероятностная сложность близка к деревьям поиска.
Списки пропусков не требуют оборотов или перемещений для вставок и обновлений и пользуются вместо этого вероятностной балансировкой. Списки пропусков обычно менее дружественны к кэшированию, нежели располагаемые в памяти B- деревья, так как узлы списка пропусков малы и размещены в памяти случайным образом. Некоторые реализации улучшают это положение дел, применяя раскрученные связанные списки.
Некий список пропусков состоит из последовательности узлов с различной высотой,
выстраивая иерархии, позволяющий пропускать диапазоны элементов. Каждый узел хранит некий ключ и, в отличии от соответствующих
узлов в связном списке, некоторые узлы могут иметь более одного наследника. Некий узел с высотой h
имеет связи от одного или более предшествующих узлов с высотой
вплоть до h. Узлы имеющегося самого нижнего
уровня могут быть связаны с узлами любой высоты.
Высота узла определяется некой случайной функцией и вычисляется в процессе вставки. Имеющие одну и ту же высоту узлы формируют некий уровень. Общее число уровней ограничивается пределом сверху во избежание непрерывного роста, а максимальная высота выбирается на основании того сколько элементов может хранить данная структура. На каждом последующем уровне имеется экспоненциально меньше узлов.
Просмотр работает путём следования по указателям встречающихся узлов на самом верхнем уровне. Как только наш поиск наталкивается на узел, который содержит ключ, который больше чем искомое значение, он следует по предшествующей ссылке на следуюий уровень. Иными словами, когда значение самого ключа больше чем значение ключа текущего узла, наш поиск продолжается далее.Когда искомый ключ меньше чем значение ключа текущего узла, поиск продолжается со следующего узла на новом уровне. Этот процесс повторяется рекурсивно до тех пор пока не обнаружен искомый ключ или его предшественник.
Например, поиск ключа 7 в нашем списке пропусков, отображаемом на Рисунке 7-8 может быть выполнен следующим образом:
-
Следует за указателем самого верхнего уровня к узлу, содержащему ключ
10. -
Так как искомый ключ
7меньше чем10, мы следуем по ссылке на следующий уровень из его головного узла, определяющей узел, содержащий ключ5. -
Мы следуем по указателю самого верхнего уровня в данном узле, определяющим узел, снова содержащем ключ
10. -
Искомый ключ
7меньше чем10и мы следуем по указателю следующего уровня, который содержит ключ5, определяющий место узла, содержащего искомый ключ7.
В процессе вставки при помощи приведённого выше алгоритма обнаруживается некая точка вставки (узел содержащий ключ или его предшественника) и содаётся новый узел. Для построения подобной дереву иерархии и сохранению баланса значение высоты данного узла определяется при помощи некого случайного числа, вырабатываемого на основании какого- то вероятносотного распределения. Указатели в предшествующем узле, содержащие ключи меньше чем значение ключа во вновь создаваемом узле связываются с точкой в этом узле. Их указатели более верхнего уровня остаются нетронутыми. Указатели во вновь создаваемом узле связываются с соответствующими последователями на каждом уровне.
В процессе удаления, следующие далее указатели удаляемого узла помещаются в предыдущий узел на соответствующие уровни.
МЫ можем создавать некую одновременную версию списка пропусков, реализуя некую линеаризуемую схему, которая пользуется
дополнитеоьным флагом fully_linked, , который определяет будут или нет указатели
соответствующего узла обновляться полностью. Этот флаг может быть установлен при помощи compare- and- swap
[HERLIHY10]. Он необходим по той причине, что указатели
рассматриваемого узла следует обновлять на множестве уровней для полного восстановления структуры данного списка
пропусков.
В языках с неуправляемой моделью памяти для обеспечения того, что имеющие ссылки в настоящее время узлы не освобождаются при одновременном доступе к ним, могут применяться счётчики ссылок или рискованные указатели (hazard pointers) [RUSSEL12]. Этот алгоритм свободен от взаимных блокировок, так как всегда имеется доступ к узлам с верхнего уровня.
Apache Cassandra применяет списки пропусков для реализации таблиц в памяти своих вторичных индексов. WiredTiger использует списки пропусков для некоторых операций в оперативной памяти.
Поскольку большая часть содержимого соответствующей таблицы располагается на диске, а устройства хранения обычно разрешают доступ блочным образом, многие реализации LSM деревьев для доступа к диску и непосредственному кэшированию полагаются на установленный кэш страниц. В разделе Управление буфером описано множество механизмов, таких как вытеснение страниц и их закрепления. причём они всё ещё применимы к хранилищу структурированного журнала.
Наиболее примечательное отличие состоит в том, что содержимое в памяти неизменно, а следовательно не требует дополнительных блокировок или защёлок для одновременного доступа. Для гарантии того, что имеющие в настоящее время страницы не будут вытеснены из памяти, используются счётчики ссылок, а выполненные ранее на лету запросы к лежащим в основе файлам удаляются в процессе уплотнения.
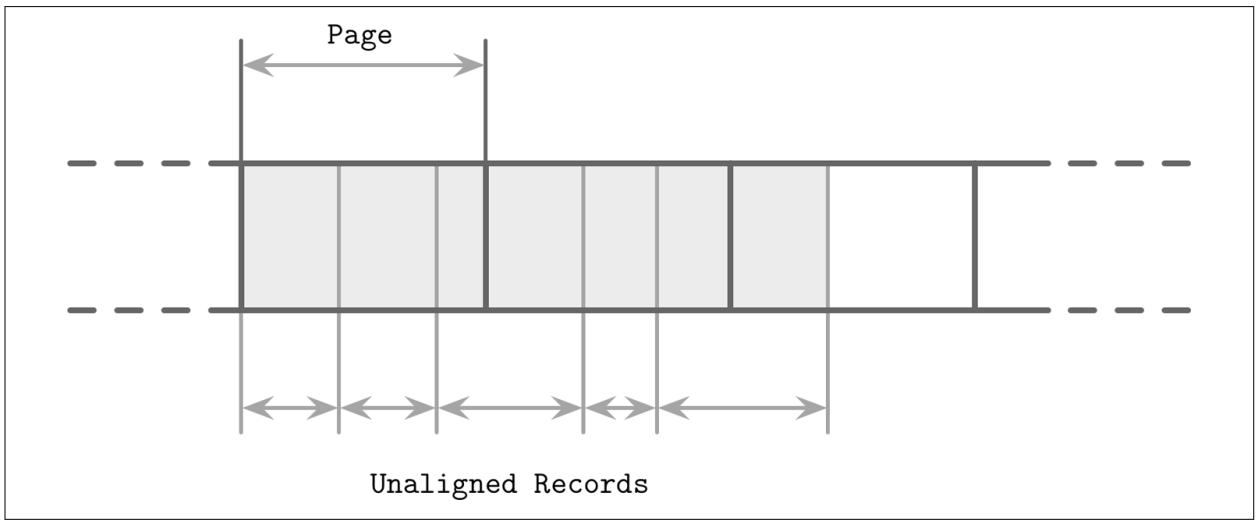
Другое отличие заключается в том, что записи данных в LSM деревьях не обязательно выравнивать по границе страниц, а указатели для адресации могут реализовываться с применением абсолютных смещений вместо идентификаторов страниц. На Рисунке 7-9 вы можете наблюдать записи с содержимым, которое не выравнено по дисковым блокам. Некоторые записи пересекают установленные границы страниц и требуют загрузки нескольких страниц в память.
В контексте B- деревьев мы уже обсуждали уплотнение (см. раздел Сжатие). Аналогичные мысли также применимы и к LSM деревьям. Основное отличие для них состоит в том, что таблицы LSM деревьев неизменны, и обычно записываются одним проходом. При упаковке данных по множеству страниц уплотняемые страницы не выровнены по границам страниц, а их размеры меньше чем у не уплотнённых.
Чтобы иметь возможность адресации к уплотнённым страницам, нам требуется отслеживать значения адресов границ при записи их содержимого. Мы можем заполнять уплотнённые страницы нулями, выравнивая их на границу страницы, однако мы утратим основные преимущества уплотнения.
Для того чтобы сделать уплотнённые страницы адресуемыми, нам требуется некий обходной путь, сохраняющий смещения и размеры уплотнённых страниц. Рисунок 7-10 отображает устанавливаемое соответствие между уплотнёнными страницами и страницами без уплотнения. Уплотнённые страницы всегда меньше своих оригиналов, ибо иначе не было бы смысла в их упаковке.
Рисунок 7-10
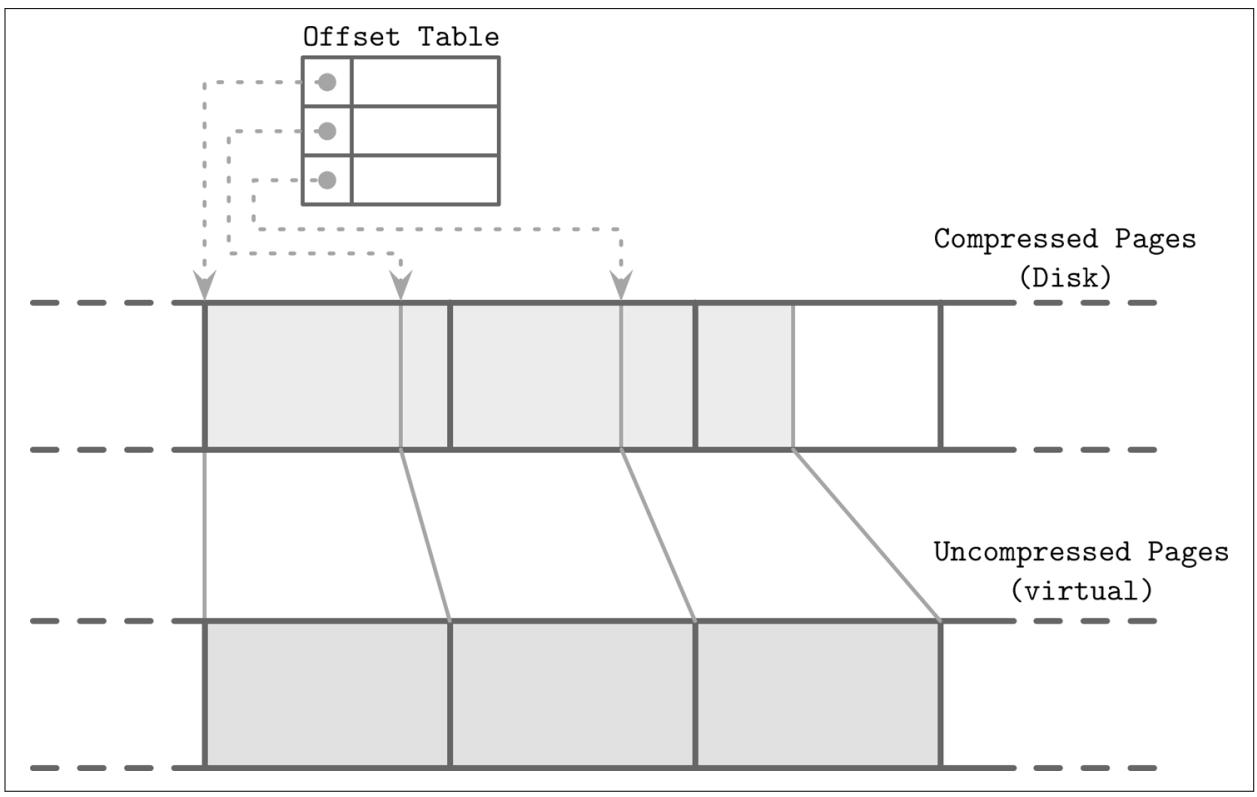
Считывание уплотнённых блоков. Пунктирные линии представляют указатели из таблицы соответствия на значения смещений уплотнённых страниц на диске. Не уплотнённые страницы обычно располагаются в имеющемся кэше страниц.
В процессе упаковки и сброса уплотнённые страницы последовательно добавляются в конец, а сведения об их упаковке (значение первоначального смещения без упаковки и реальное значение смещения уплотнённой страницы) сохраняются в неком отдельном сегменте файла. В процессе самого считывания, отыскиваются смещение данной упакованной страницы и её размер, а страница может быть раскрыта и материализована в памяти.
Большинство до сих пор обсуждавшихся структур хранения хранили данные упорядоченно. Изменяемые и неизменяемые страницы B-деревьев, сортированные прогоны в FD деревьях, а также SSLTables в LSM деревьях хранят данные в порядке своих ключей. Сам порядок в этих структурных сохраняется различным образом: страницы B- дерева обновляются по месту хранения, прогоны FD- дерева создаются слиянием двух прогонов, а SSLTables создаются буферизацией и сортировкой записей данных в памяти.
В данном разделе мы обсудим структуры, хранящие записи в произвольном порядке. Неупорядоченные хранилища обычно не требуют отдельного журнала и допускают снижения стоимости записей сохранением данных неупорядоченным образом.
Bitcask,, один из механизмов хранения, применяемых в Riak, является неким механизмом хранения структурированного журнала без упорядочения [SHEEHY10b]. В отличии от обсуждавшихся до сих пор реализаций хранилищ структурированных журналов, он не применяет таблицы в памяти для буферизации и сохраняет записи данных напрямую в файлах журналов.
Для тгбо чтобы сделать возможным поиск значений, Bitcask применяет некую структуру с названием keydir, которая хранит ссылки на самые последие записи данных для значений соответствующих ключей. Старые записи данных всё ещё могут присутствовать на диске, однако на них нет ссылок из keydir и они подвержены сборке мусора в процессе уплотнения. Keydir реализуется как некое соответсвие хэш- значений в памяти и должно повторно строиться из имеющихся файлов журналов в процессе запуска.
В процессе некой записи некие ключ и запись данных последовательно добавляются в имеющийся файл журнала, а указатель на местоположение этой вновь созданной записи данных помещается в keydir.
Считывание проверяет keydir на предмет определения места искомого ключа и следует по полученному связанному с ним указателю в соответствующий файл журнала, определяя местоположение записи данных. Поскольку в определённый момент времени в данном keydir может иметься лишь одно связанное с искомым ключом значение, запросы точки не должны сливать данные из множества источников.
Рисунок 7-11 показывает соответствие между самими ключами и записями в файлах данных Bitcask. Файлы журнала содержат записи данных, а keydir указывает на самую последнюю живую запись данных, связанную с каждым ключом. Экранированные записи в файлах данных (те, которые были замещены более поздними записями или удалениями) отображены серым.
Рисунок 7-11
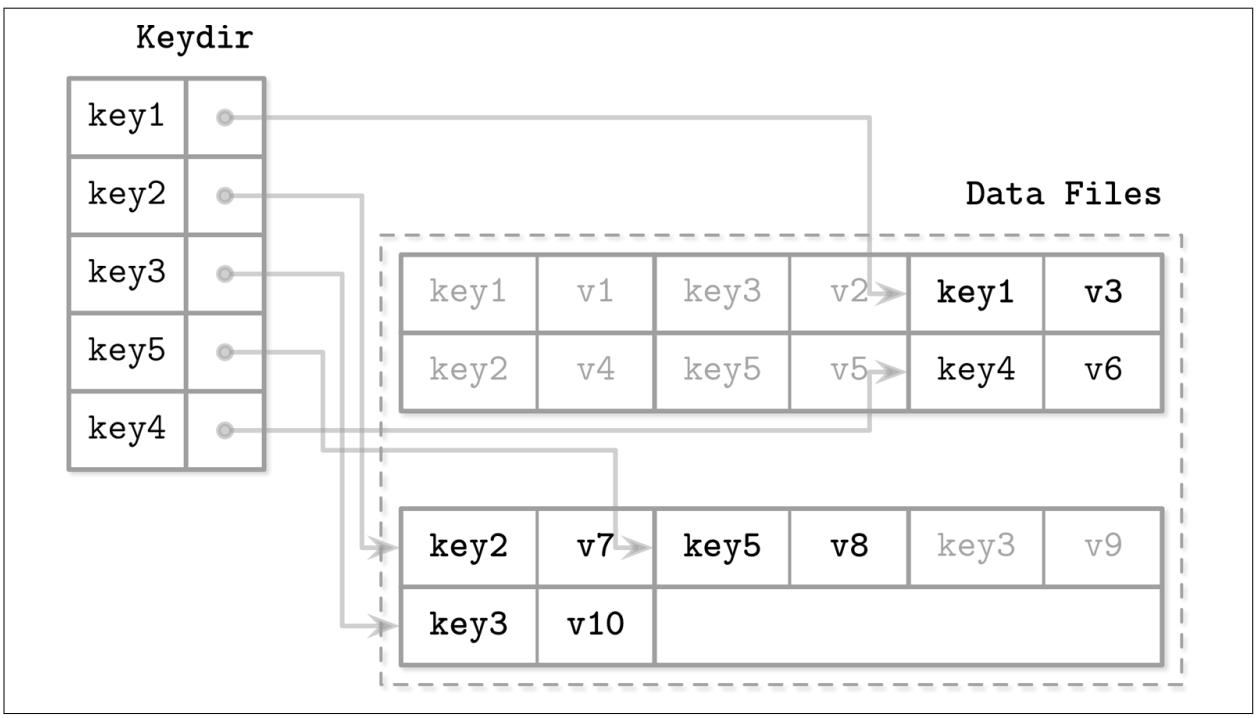
Соответствие между keydir и файлами данных в Bitcask. Сплошные линии представляют указатели от самого ключа к самому последнему связанному с ним значению. Скрытые пары ключ/ значение показаны светло серыми.
В процессе уплотнения, содержимое всех файлов журналов последовательно считывается, сливается и записывается по новому месту, представляя лишь живые записи данных и отбрасывая все экранированные. Keydir обновляется новыми указателями на перемещённые записи данных.
Записи данных сохраняются непосредственно в файлах журнала, поэтому не требуется сопровождение отдельного журнала упреждающей записи, что снижает как накладные расходы пространства, так и увеличение записей. Некой изнанкой этого подхода является то, что он предлагает лишь точечные запросы и не допускает сканирование диапазонов, поскольку элементы не сортированы как в keydir, так и в файлах данных.
Преимуществами данного подхода выступают простота и великолепная производительность точечных запросов. Даже когда существует множество версий записей данных, через keydir адресуется только самая последняя. Тем не менее, необходимость отслеживания в памяти всех ключей и перестроение keydir при запуске являются ограничениями, которые способны выступать препятствующими условиями для некоторых вариантов применения. Хотя данный подход и великолепен для точечных запросов, он не предлагает никакого сопровождения для запросов диапазонов.
Запросы диапазонов важны для многих приложений и было бы великолепно иметь некую структуру хранения, которая бы обладала преимуществами записи и пространства не сортированных хранилищ, и в то же время позволяла бы нам сканирование диапазонов.
WiscKey [LU16] отвязывает сортировку от сборки мусора, сохраняя значения ключей сортированными в LSM деревьях и оставляя записи данных в не сортированных файлах с добавлением в конец, именуемые как vLogs (value logs, журналы значений). Такой подход способен разрешить две проблемы, упомянутые при обсуждении Bitcask: необходимость удержания всех ключей в памяти и перестроения некой таблицы хэширования при запуске.
Рисунок 7-12 отображает ключевые компоненты WiscKey и соответствие между ключами и файлами журналов. Файлы vLogs хранят не сортированные записи данных. Ключи хранятся в сортированных LSM деревьях, указывая на самые последние записи данных в соответствующих файлах журналов.
Рисунок 7-12
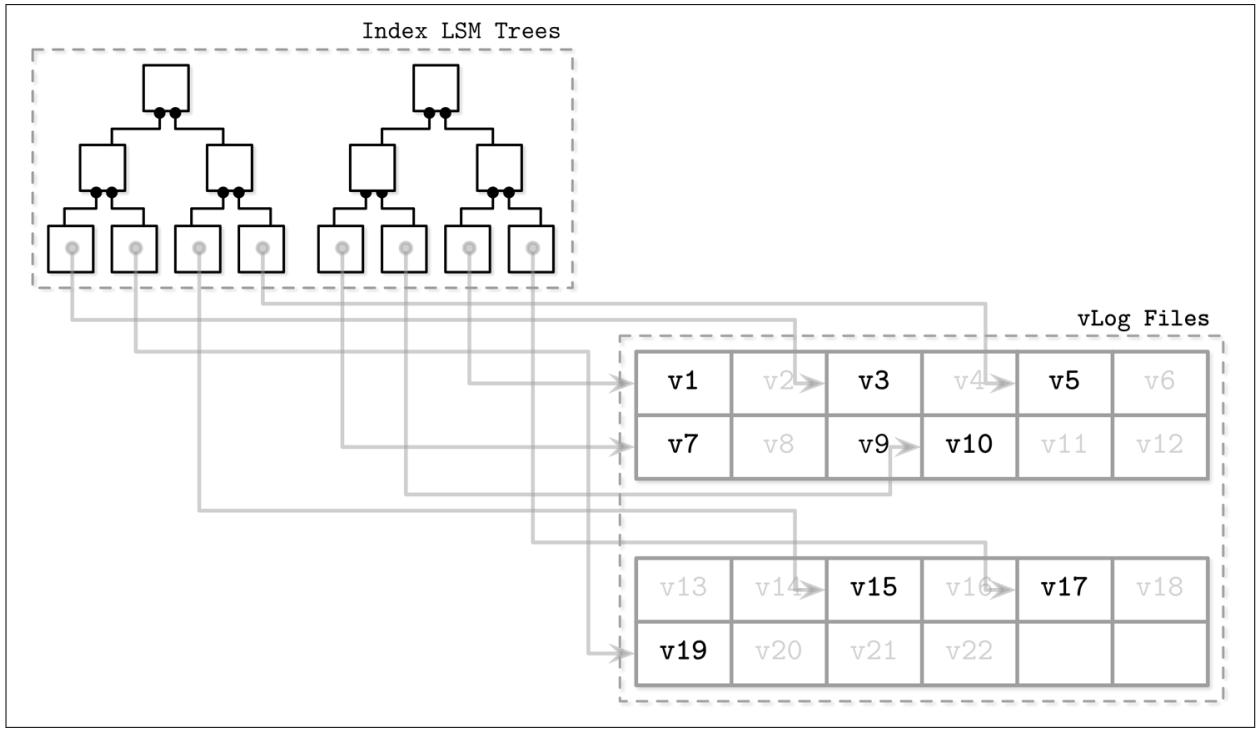
Ключевые компоненты WiscKey: индекс LSM деревьев и файлы vLog, а также взаимоотношения между ними. Скрытые записи в файлах данных (которые мы впоследствии делим на записываемые и удаляемые) показаны серым. Сплошные линии представляют указатели от соответствующего ключа в самом LSM дереве к самому последнему значению в его файле журнала.
Поскольку обычно ключи намного меньше чем связанные с ними записи данных, их уплотнение намного более действенное. Это подход может в частности быть полезным для вариантов применения с низкой скоростью обновлений и удалений, при которых сборка мусора не способна высвобождать большие объёмы пространства диска.
Самый основной вызов здесь состоит в том, что данные vLog не сортированы, сканирования чтения требуют произвольного ввода/ вывода. WiscKey применяет внутренний парралелизм SSD для предварительной параллельной выборки блоков на протяжении сканирований диапазона и снижает стоимости ввода/ вывода. В терминах блочного обмена, эти стоимости всё ещё высоки: для выборки некой отдельной записи данных в процессе необходимого сканирования диапазона, подлежит считыванию вся страница, в которой она содержится.
В процессе уплотнения, содержимое файла vLog последовательно считывается, сливается и записывается по новому месту.
Указатели (значения ключа в LSM дереве) обновляются на точку для этого нового местоположения. Во избежание сканирования
всего vLog, WiscKey пользуется указателями head и
tail, содержащими сведениями относительно сегментов vLogs, которые хранят
живые ключи.
Поскольку данные в vLogs не сортированы и не содержат сведений о жизнеспособности, приходится сканировать само дерево ключей для определения того какие из значений всё ещё живы. Выполнение таких проверок на протяжении сборки мусора вводит дополнительную сложность: традиционные LSM деревья могут разрешать содержимое файла в процессе уплотнения без адресации значения индекса ключа.
Основные проблемы с одновременностью в LSM деревьях связаны с переключением на табличное представление (table view, собрание располагаемых в памяти и на диске таблиц, которые изменились в процессе сброса и упаковки) и синхронизации журнала. Доступ к таблицам в памяти также, как правило, выполняется одновременно (за исключением хранилищ с разбитым на разделы ядром, таких как ScyllaDB), однако одновременные в памяти структуры данных выходят за рамки данной книги.
В процессе сброса необходимо следовать следующим правилам:
-
Сами новые таблицы в памяти должны стать доступными для чтений и записей.
-
Старые (сбрасываемые) таблицы в памяти должны оставаться видимыми для чтений.
-
Сбрасываемые таблицы в памяти должны быть записаны на диск.
-
Отбрасывание сброшенных таблиц в памяти и превращение сброшенных страниц в располагаемые на диске необходимо выполнять некой атомарной операцией.
-
Имеющийся сегмент журнала упреждающего чтения, удерживающего записи журнала применённых операций к сброшенным таблицам в памяти обязан быть отброшен.
К примеру, Apache Cassandra решает эти задачи применяя операции упорядоченных барьеров: все принятые на запись операции будут ожидать пока прежде не сбросится соответствующая таблица в памяти. Таким образом, сам процесс сброса (обслуживаемый как потребитель) знает какие прочие процессы (выступающие в роли поставщиков) полагаются на него.
В более общем случае у нас имеются следующие точки синхронизации:
- Переключение таблиц в памяти
После него все записи происходят только в новой таблице в памяти, которая сделана первичной, в о время как старая всё ещё доступна для чтения.
- Завершение сброса
Заменяет в установленном табличном представлении свою старую таблицу в памяти сброшенной располагаемой на диске.
- урнал транзакций упреждающей записи
Отбрасывает сегмент журнала со сброшенной располагаемой на диске таблицей в установленном представлении таблицы.
Эти операции должны строго следовать установкам реализации. Продолжение записей в имеющуюся старую таблицу в памяти может иметь результатом потерю данных; например, когда такая запись выполняется в некий раздел таблицы в памяти, который уже сброшен. Аналогично, ошибочно не оставляя свою старую таблицу в памяти доступной на чтения, пока не будет готова её располагаемая на диске противоположность, приведёт в результате к незавершённым результатам.
В процессе упаковки имеющееся представление таблицы также изменяется, однако здесь этот процесс слегка более прямолинеен: старые располагаемые на диске таблицы отбрасываются, а вместо них добавляется соответствующая уплотнённая версия. \старые таблицы должны оставаться доступными для чтений пока не будут полностью записаны новые и не станут готовыми заменить их для считываний. Ситуации, при которых одни и те же таблицы участвуют во множестве запущенных параллельно упаковках также следует избегать.
В B- деревьях усечение журнала следует рассматривать координируемым со сбросом испорченных (dirty) страниц из установленного кэша страниц для обеспечения долговечности. В LSM деревьях у нас имеется аналогичное требование: записи буферируются в таблицах в памяти и их содержимое не долговечно до выполнения соответствующего сброса, а в случае крушения узла содержимое журнала не будет воспроизведено и невозможно будет восстановить данные этого сегмента.
Отсутствие синхронизации усечения журнала со сбросом также приведёт в результате к потере данных: если некий сегмент журнала отброшен до завершения его сброса, а этот узел испытывает крушение, содержимое журнала невозможно воспроизвести и данные этого сегмента невозможно восстановить.
Многие современные файловые системы снабжены структурированным журналом: они буферируют записи в сегменте памяти и сбрасывают его содержимое на диск по мере его заполнения неким образом дописывания в конец. Чтобы иметь дело с небольшими произвольными записями, также применяются хранилища структурированного журнала на SSD, что минимизирует накладные расходы записи, улучшая уровень износа и увеличивая время службы данного устройства.
Системы хранения со структурированным журналом (LSS, log-structured storage) начинают обретать популярность со временем, когда SSD становятся более доступными. LSM деревья и SSD хорошо подходят друг к другу, поскольку последовательные рабочие нагрузки и исключительная запись в конец способствуют снижению роста обновлений по месту хранения, что отрицательно сказывается на производительности SSD.
Когда мы помещаем в стек множество систем структурированного журнала, одна поверх другой, мы можем врезаться в некоторые проблемы, которые мы и пытались решать применяя LSS, включая рост записей, фрагментирование и плохую производительность. По крайней мере, нам следует хранить в памяти соответствующий уровень трансляции флеш SSD и его файловой системы при разработке своих приложений [YANG14].
Применение некоего уровня соответствия структурированного журнала в SSD мотивируется двумя обстоятельствами: небольшие произвольные записи следует совместно объединять в пакеты в некую физическую страницу, а также тот факт, что SSD работают применяя циклы программирования/ уничтожения. Записи могут выполняться только в предварительно уничтоженные (erased) страницы. Это означает, что такая страница не может быть запрограммирована (иными словами, записана), пока она не очищена (иначе говоря, не уничтожена).
Отдельная страница не может быть уничтожена, причём лишь сгруппированные в некий блок (обычно содержащий от 64 до 512 страниц) может быть совместно уничтожен. Рисунок 7-13 отображает некое схематичное представление страниц, группируемых в некий блок. Уровень трансляции сброса (FTL, flash translation layer) транслирует логические адреса страниц в их физическое расположение и отслеживает состояние страниц (рабочие, отброшенные или пустые). Когда FTL исчерпывает свободные страницы, ему приходится выполнять сборку мусора и уничтожать отвергнутые страницы.
Нет никаких гарантий, что все страницы в том блоке, который готов к уничтожению отвергнуты. Прежде чем этот блок будет очищен, FTL придётся передислоцировать свои рабочие (live) страницы в один из блоков, содержащих пустые страницы. Рисунок 7-14 отображает такой процесс перемещения рабочих страниц из одного блока в новое местоположение.
После того как все рабочие страницы передислоцированы, этот блок может быть безопасно очищен (уничтожен), а его свободные страницы становятся доступными для записи. Поскольку FTL осведомлён о состояниях страниц и переходах состояний, а также обладает всеми необходимыми сведениями, он также отвечает за износ (wear leveling) SSD.
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Износ распространяет в конечном итоге нагрузку по всему носителю, избегая горячих точек, при которых блоки отказывают окончательно по причине большого числа циклов программирования уничтожения. Это необходимо, так как ячейки флеш памяти способны проходить лишь ограниченное число циклов программирования очистки и равномерное использование ячеек памяти способствует расширению времени жизни данного устройствва. |
В итоге, основной мотивацией применения хранилища структурированного журнала в SSD служит амортизации стоимостей ввода/ вывода путём объединения совместно в пакеты небольших произвольных записей, что обычно приводит в результате к меньшему числу операций и, следовательно, к снижению числа раз включения сборки мусора.
Поверх этого мы получаем файловые системы, многие из которых также применяют техники журналирования для буферизации записи с целью снижения роста записей и оптимального использования лежащего в основе оборудования.
Стекирование журнала проявляется несколькими различными способами. Во- первых, каждый уровень должен выполнять свою собственную бухгалтерию и в большинстве случаев такие лажащие в основе журналы не выставляют свои сведения, необходимые во избежание дублирования усилий.
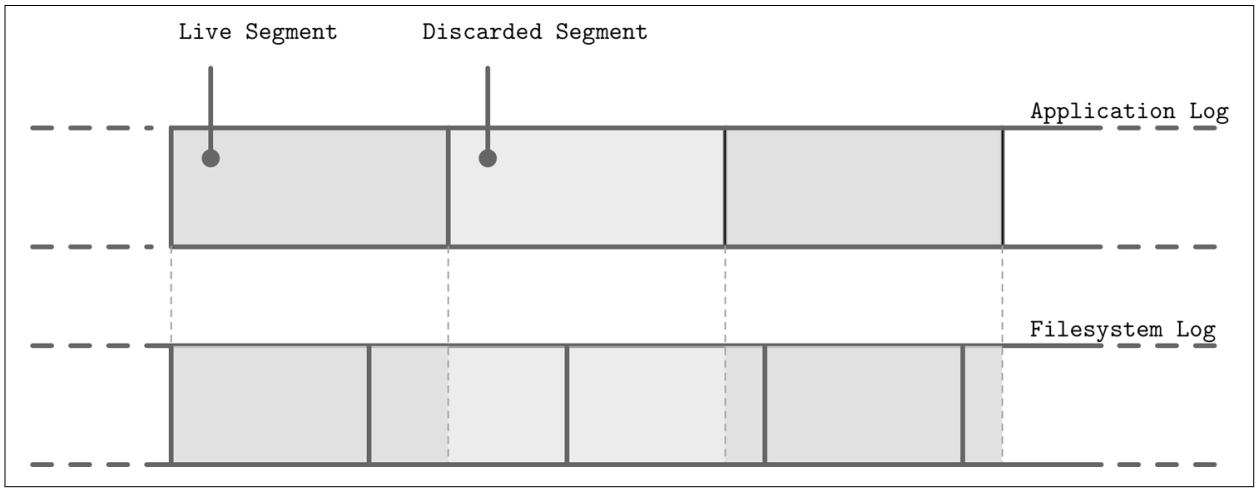
Рисунок 7-15 показывает соответствие между неким журналом верхнего уровня (например, уровня приложения) и журналом нижнего уровня (скажем, его файловой системы), имеющим в результате избыточное протоколирование и различные шаблоны сборки мусора [YANG14]. Записи не совпадающих сегментов могут приводить к ещё худшим обстоятельствам, при которых отбрасывание сегмента журнала верхнего уровня может вызывать фрагментирование и передислокацию имеющихся соседними частей сегментов.
Поскольку уровни не взаимодействуют с относящимся к LSS расписанию (к примеру, отбрасыванию или передислокации сегментов), подсистемы нижнего уровня могут выполнять избыточные операции по отбрасыванию данных или близких к отбрасыванию данных. Аналогично, по причине отсутствия единого, стандартного размера сегмента, может случиться, что не выровненные сегменты верхнего уровня занимают множество сегментов нижнего уровня. Все эти накладные расходы могут быть снижены, или же их можно полностью избегать.
Даже хотя мы и говорим, что хранилище структурированного журнала целиком посвящено последовательному вводу/ выводу, мы должны держать на уме, что системы баз данных могут обладать множеством потоков записи (скажем, журналы параллельно сохраняют записи данных) [YANG14]. При рассмотрении на аппаратном уровне, перекрывающиеся потоки последовательных записей могут не транслироваться в те же самые последовательные шаблоны: блоки не обязательно помещаются в порядке их записи. Рисунок 7-16 отображает множество перекрывающихся по времени потоков, сохраняющих записи, обладающие размерами, не выровненными на размер страницы лежащего в основе оборудования.
В результате мы получаем фрагментирование, которого мы пытались избежать. Для снижения перекрытий некоторые производители баз данных рекомендуют хранить сам журнал на отдельном устройстве для изолирования рабочих нагрузок и чтобы получать обоснованные значения их производительности и шаблонов доступа независимым образом. Тем не менее, более важно сохранять выравнивание разделов для лежащего в основе оборудования [INTEL14] и сохранять записи выровненными на размер страниц[KIM12].
Хорошо, вы никогда не поверите в это, но та лама, которую вы видите когда- то была человеком. и не просто человеком. Этот парень был императором. Богатым, раздутым от божественной силы.
- Кузко из Новой борозды императора
В разделе Bw- деревья мы обсуждали не изменяемую версию B- дерева с названием Bw- дерева. Bw- деревья выстраиваются уровнем поверх подсистемы хранения свободной от защёлок со структурированным журналом и осведомлённой о методе доступа (LLAMA, latch-free, log-structured, access-method aware). Такой уровень позволяет Bw- деревьям динамично расти и сокращаться, в то же время оставляя сборку мусора и управление страницами прозрачными для самого дерева. В данном случае мы больше всего интересуемся в части осведомлённости о методе доступа, демонстрирующем основные преимущества координации между имеющимися программными уровнями.
В качестве резюме, некий логический узел Bw- дерева состоит из связанного списка физических узлов данных, некой цепочки обновлений от самого нового вплоть до самого старого., в конечном итоге имея некий базовый узел. Логические узлы связаны при помощи таблицы соответствия в памяти, указывающей на местоположение самого последнего обновления на диске. Ключи и значения добавляются и удаляются из соответствующего логического узла, однако их физическое представление остаётся неизменным.
Хранилища структурированного журнала буферируют изменения узла (узлы приращений) совместно в неком 4МБ флэш- буфере. Как только эта страница заполнена, она сбрасывается на диск. Периодически сборка мусора возвращает пространство, занимаемое не используемыми узлами приращений и базовыми узлами и передислоцирует все рабочие в свободные страницы без фрагментирования.
Без наличия осведомлённости о методе доступа перекрывающиеся узлы приращений,которые относятся к различным логическим узлам, будут записываться в их порядке вставки. Оседомлённость Bw- деревьев в LLAMA допускает консолидацию различных узлов приращений в неком отдельном непрерывном физическом месте. Когда два обновления в узлах приращения прекращают друг друга (например, за некой вставкой следует удаление), также мжно выполнять их логическую консолидацию, и может оставаться лишь последнее удаление.
Сборка мусора LSS также может заботиться о консолидации содержимого своего логического узла Bw- дерева. Это означает, что сборка мусора не только будет возвращать пустое пространство, но также значительно снижать имеющееся фрагментирование физического узла. Если бы сборка мусора лишь перезаписывала непрерывно определённые узлы приращений, она всё ещё занимала бы то же самое пространство, а читателям приходилось бы выполнять работу по применению обновлений приращениями к своему базовому узлу. В то же самое время, когда система более верхнего уровня выполняет консолидацию имеющихся узлов и непрерывно записывает их в новом месте, LSS всё ещё будет собирать мусор своих старых версий.
Будучи осведомлёнными о семантике Bw- дерева, определённые приращения могут быть перезаписаны в отдельный базовый узел со всеми уже применёнными приращениями в процессе сборки мусора. Это снижает общий размер пространства, используемого для представления такого узла Bw- дерева и значение задержки, необходимой для считывания самой страницы при возврате того пространства, которое занято отвергаемыми страницами.
Вы можете видеть, что при аккуратном подходе, стекирование всё ещё может давать множество преимуществ. Нет необходимости всегда строить туго стянутые структуры с единственным уровнем. Хороший API и выставление правильных сведений способно существенно улучшать эффективность.
Некой альтернативой стекируемым программным уровням является пропуск всех косвенных уровней и использование аппаратных средств напрямую. Например, имеется возможность избегать применения файловой системы и уровня трансляции сброса выполняя разработку в Open- Channel SSD. Тем самым мы можем избежать по крайней мере двух уровней журналов и обладать большим контролем над износом, сборкой мусора размещением данных и планированием. Одной из реализаций, применяющих такой подход, является LOCS (LSM Tree-based KV Store on Open-Channel SSD) [ZHANG13]. Другим примером использования Open-Channel SSD является LightNVM, реализованный в самом ядре Linux [BJØRLING17].
Уровень трансляции сброса обычно обрабатывает размещение данных, сборку мусора и передислокацию страниц. Open-Channel
SSD выставляет их внутренне присущие свойства, управление устройством и расписания ввода/ вывода без необходимости проходить
через FTL. Хотя это и требует намного большего внимания к подробностям с точки зрения разработчика, такой подход
способен давать значительные улучшения производительности. Вы можете провести параллель с применением флага
O_DIRECT для обхода имеющегося кэширования страниц в самом ядре, который
даёт лучший контроль, но требует ручного управления страницами.
Software Defined Flash (SDF) [OUYANG14], совместно с Open Channel SSD разрабатываемая система аппаратных/ программных средств, выставляет асимметричный интерфейс ввода/ вывода, который учитывает специфические особенности SSD. Размеры элементов чтения и записи различны, причём размер элемента записи соответствует размеру элемента удаления (блоку), что значительно снижает рост записей. Эти установки идеальны для хранилища со структурированным журналом, так как существует лишь единственный программный уровень, который выполняет сборку мусора и размещение страниц. Кроме того, разработчики имеют доступ к внутреннему параллелизму SSD, так как каждый канал в SDF выставляется как некое отдельное блочное устройство, которое может применяться для дальнейшего улучшения производительности.
Сокрытие сложности за неким простым API может звучать интригующим, однако способно вызывать осложнения на тех программных уровнях, которые имеют различные семантические правила. Выставление некоторых лежащих в основе внутренних системных возможностей может иметь преимущества для лучшей интеграции.
Хранилище со структурированным журналом применяется повсеместно: от уровня трансляции сброса до файловых систем и систем баз данных. Он помогает снижению роста записей собирая в пакет совместно в памяти небольшие произвольные записи. Для возврата занимаемого удаляемыми сегментами пространства, LSS периодически включают сборку мусора.
LSM деревья берут некие идеи из LSS и способствуют построению индексных структур управляемых в стиле структурированного журнала: записи собираются в пакеты в памяти и сбрасываются на диск; экранированные записи данных вычищаются в процессе уплотнения.
Важно запомнить, что многие программные уровни применяют LSS и убедиться что уровни оптимально собраны в стек. В качестве альтернативы, мы можем пропустить вообще уровень файловой системы и осуществлять доступ к аппаратным средствам напрямую.
![[Замечание]](/common/images/admon/note.png) | Последующее чтение |
|---|---|
|
Если вы желаете узнать больше относительно упоминавшихся в этой главе понятий, вы можете ссылаться на следующие источники:
|
В части 1 я обсудил механизмы хранения. Мы начали с архитектуры верхнего уровня систем баз данных и их классификации, изучили как реализовывать дисковые структуры хранения и как они вписываются в общую картину с прочими компонентами.
Я рассмотрел некоторые структуры хранения, начав с B- деревьев. Рассмотренные структуры не представляют все поле целиком, и имеется множество прочих интересных разработок. Тем не менее, данные примеры всё ещё хорошая иллюстрация трёх основных свойств, которые мы выделили в самом начале этой части: буферизации, неизменности и упорядоченности. Эти свойств полезны для описания, запоминания и выражения различных сторон имеющихся структур хранения.
Таблица I-1 суммирует обсуждённые структуры хранения и показывает используют или нет они эти свойства.
| Буферируемые | Изменяемые | Упорядоченные | |
|---|---|---|---|
B+ деревья |
Нет |
Да |
Да |
WiredTiger |
Да |
Да |
Да |
LA- деревья |
Да |
Да |
Да |
COW B- деревья |
Нет |
Нет |
Да |
2C LSM- деревья |
Да |
Нет |
Да |
MC LSM- деревья |
Да |
Нет |
Да |
FD- деревья |
Да |
Нет |
Да |
BitCack |
Нет |
Нет |
Нет |
WiscKey |
Да(1) |
Нет |
Да(1) |
BW- деревья |
Нет |
Нет |
Нет(2) |
Добавление буферизации в памяти всегда носит положительное воздействие на рост зарисей. При обновлении структур по месту хранения, таких как WiredTiger и LA-Trees, буферизация в памяти способствует амортизации общей стоиомсти множества записей в одной и той же странице через их комбинирование. Иными словами, буферизация помогает снижению роста записей.
В неизменных структурах, таких как многокомпонентные LSM деревья и FD- деревья буферизация носит аналогичный положительный эффект, однако за счёт последующих перезаписей при перемещении данных с одного неизменного уровня на другой. Иначе говоря, применение неизменности имеет некое положительное воздействие на одновременность и рост пространства, так как большинство обсуждённых неизменяемых структур используют полностью занятые страницы.
При использовании неизменности, пока мы также не применяем буферизацию, мы в конце концов приходим к неупорядоченным структурам, таким как BitCack и WiscKey (за исключением копируемых- записью B- деревьев с копированием, вторичной сортировкой и передислокацией их страниц). WiscKey хранит только ключи в сортированных LSM деревьях и позволяет выборку записей в порядке ключей применяя индексацию ключей. В Bw- деревьях некоторые из имеющихся узлов (те, которые были консолидированы) хранят записи данных в порядке ключей, в то время как все прочие имеющиеся логические узлы Bw- дерева могут иметь свои приращения обновлений разбросанными по различным страницам.
Вы видите, что эти три свойства могут перемешиваться и соответствовать порядку для достижения желательных характеристик. К несчастью, архитектура механизма хранения обычно вовлечена в компромиссы: вы увеличиваете общую стоимость одной операции в угоду другой.
Применяя эти знания, вы должны быть способны начать ближе понимать сам код большинства современных систем баз данных. Некоторые ссылки на такой код и отправные точки можно найти по всей книге. Знание и понимание приводимой терминологии сделает для вас этот процесс более быстрым.
Многие современные системы баз данных усилены вероятностными структурами данных [FLAJOLET12] [CORMODE04], а также имеются новые исследования, выполненные привнесёнными в системы баз данных идеями из машинного обучения [KRASKA18]. Мы близки к изучению последующих изменений в исследованиях и отрасли, таких как энергонезависимые и байт- адресуемые хранилища, становящиеся всё более распространёнными и более широко доступными [VENKATARAMAN11].
Знание тех фундаментальных понятий , которые описаны в этой книге должно помочь вам понять и реализовать более новые исследования, та как они заимствуют, строятся поверх и вдохновляются теми же самыми понятиями. Основное преимущество знание этой теории и истории состоит в том, что ничто не бывает целиком новым и, как показывает изложение данной книги, прогресс идёт поступательно увеличиваясь.