Глава 6. Варианты B- деревьев
Содержание
Вариации B- деревьев обладают в целом некоторыми общими моментами: древовидной структурой, балансировкой через расщепления и слияния, а также алгоритмами поиска и удаления. Прочие подробности, относящиеся к одновременности, представлению дисковых страниц, связей между узлами одного уровня и процессами поддержки могут разниться между реализациями.
В этой главе мы обсудим некоторые технологии, которые могут применяться для реализации действенных B- деревьев и структур, которые они предоставляют:
-
B- деревья копирования- записью подобны структурам B- деревьев, однако их узлы неизменны и не обновляются по месту расположения. Вместо этого страницы копируются, обновляются и записываются в новом месте.
-
Ленивые B- деревья снижают число запросов ввода/ вывода последовательных записей в одном и том же узле буферируя обновления в узлах. В своей следующей главе мы также обсудим двухкомпонентные деревья LSM (см. Двухкомпонентные LSM деревья), которые предпринимают дальнейший шаг буферизации при реализации полностью неизменных B- деревьев.
-
Деревья FD предпринимают иной подход для буферизации, в чём- то схожий с деревьями LSM (см. Деревья LSM). FD- деревья обновляют буфер в небольшом B- дереве. Как только такое дерево заполняется, его содержимое записывается в неком неизменном исполнении. Обновления распространяются между уровнями неизменных исполнений неким каскадным образом, причём от более верхних уровней к нижним.
-
Деревья Bw делят узлы B- дерева на некоторые части меньшего размера, которые записываются неким манером добавления в конец. Это снижает стоимости записей меньшего размера упаковывая совместно обновления различных узлов.
-
Не замечающие кэш B- деревья позволяют рассматривать дисковые структуры данных неим образом, который очень похож с тем, как мы выстраиваем их в оперативной памяти.
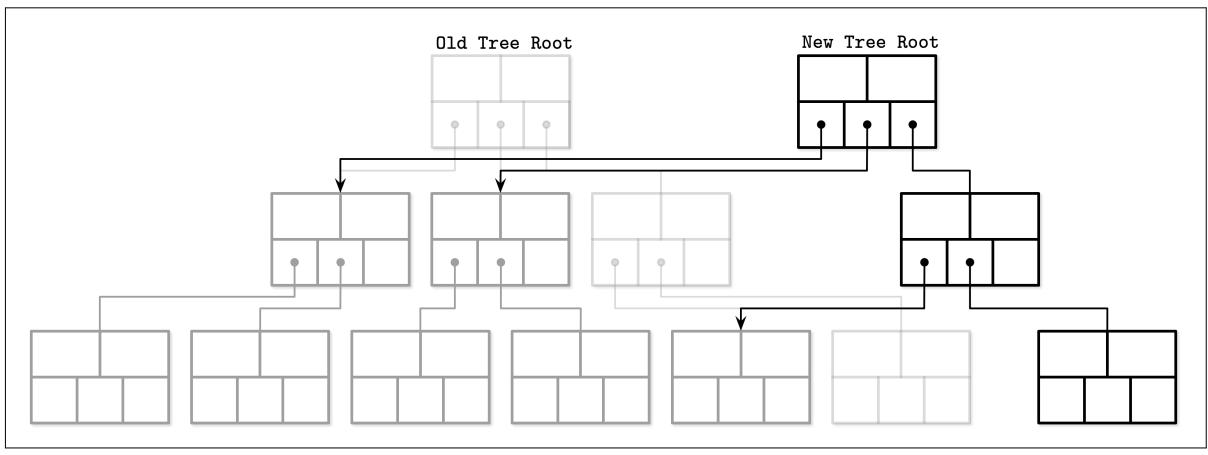
Некоторые базы данных вместо того чтобы строить сложные механизмы защёлок пользуются технологией копирования- записью (copy- on- write) для обеспечения целостности в присутствии одновременных операций. В этом случае всякий раз когда изменяется определённая страница, её содержимое копируется, вместо самой первоначальной страницы изменяется эта скопированная страница и создаётся иерархия параллельного дерева.
Старые версии дерева остаются доступными для читателей, которые работают одновременно с этим писателем, в то время как получающие доступ писатели вынуждены ждать пока не завершатся предыдущие операции записи. После создания такой новой иерархии страниц, автоматически обновляется значение указателя на самую верхнюю страницу. На Рисунке 6-1 вы можете видеть некое новое дерево, созданное параллельно со старым, повторно использующим не тронутые страницы.
Очевидной обратной стороной данного подхода является то,что он требует больше пространства (даже несмотря на то, что старые версии сохраняются лишь на протяжении короткого временного периода, поскольку страницы могут быть возвращены немедленно по завершению одновременных операций, использующих старые страницы) и процессорного времени, так как требуется копирование всего содержимого страницы. Благодаря обычно относительно малой глубине B- деревьев, предлагаемые простота и преимущества данного подхода обычно перевешивают имеющиеся отрицательные моменты.
Самым большим преимуществом данного подхода является то, что читатели не нуждаются в синхронизации, ибо доступ к записанным страницам может осуществляться немедленно без дополнительных защёлок. Поскольку записи выполняются в скопированных страницах, читатели не блокируются писателями. Никакие действия не мгут обозревать страницу в незавершённом состоянии, а крушение системы не способно оставлять страницы в неком разрушенном состоянии, так как самый верхний указатель переключается лишь когда выполнены все изменения страницы.
Одним из имеющихся механизмов хранения, применяющих копирование- записью, является Облегчённая отображаемая в памяти база данных (LMDB, Lightning Memory-Mapped Database), которая является хранилищем ключ- значение, используемым в проекте OpenLDAP. Благодаря своим проектным возможностям и архитектуре, lDMB не требует некого кэша страниц, журнала упреждающей записи, контрольных точек и сжатия (Для получения дополнительных сведений по LDMB, ознакомьтесь с комментариями к коду и презентацией).
LMDB реализуется как некое хранилище данных с единственным уровнем, что означает, что операции чтения и записи удовлетворяются непосредственно через имеющееся соответствие в памяти, причём без дополнительного уровня кэширования в промежутке. Это также означает, что страницам не требуется дополнительная материализация и чтения могут обслуживаться непосредственно в самом соответствии в памяти без копирования данных в требуемый иначе промежуточный буфер. В процессе выполнения обновления, все узлы ветвления во всём пути от самого корня до искомого целевого листа копируются и потенциально изменяются: изменяются узлы, на которые распространяются обновления, а все остальные узлы остаются нетронутыми.
LMDB хранит только две версии своего узла корня: самую последнюю версию и ту, которая предназначена для фиксации новых изменений. Этого достаточно, так как всем записи приходится проходить через свой узел корня. После создания нового узла корня, старый становится недоступным для новых чтений и записей. Как только завершены все чтения, обратившиеся к разделам старого дерева, их страницы возвращаются и могут использоваться повторно. Благодаря тому что LMDB спроектирована с исключительным добавлением в конец, она не пользуется ссылками одного уровня и ей приходится восходить обратно к своему родительскому узлу в процессе последовательных сканирований.
При данном подходе оставлять сворованные сведения в скопированных узлах непрактично: уже имеется некая копия, которая может использоваться для MVCC и подходить происходящим в настоящий момент транзакциям чтения. Сама структура базы данных внутренним образом снабжена множеством версий и читатели могут работать без каких бы то ни было блокировок, поскольку им не требуется ни коим образом взаимодействовать с писателями.
Для обновления тем или иным путём определённой страницы на диск нам вначале приходится обновлять её представление в памяти. Тем не менее, существует несколько способов представления некого узла в памяти: мы можем получать непосредственный доступ к имеющейся кэшированной версии определённого узла, выполняя его через соответствующий обёртывающий объект, либо естественным образом создавать его представление в памяти для самого языка программирования реализации.
В языках программирования с некой неуправляемой моделью памяти, хранимые в узлах B- дерева сырые двоичные данные могут повторно интерпретироваться и для манипулирования ими могут применяться их естественные указатели. В таком случае данный узел определяется в терминах структур, которые пользуются сырыми двоичными данными за самим указателем и явными преобразованиями типов времени исполнения. В большинстве случаев они указывают на соответствующую область памяти, управляемую самим кэшем страниц или пользуются соответствиями в оперативной памяти.
В качестве альтернативы узлы B- дерева могут материализовываться в объектах или структурах, которые внутренне присущи языку программирования. Эти структуры могут применяться для вставок, обновлений и удалений. В процессе сброса изменения применяются в страницам в памяти и после этого на диске. Такой подход имеет основное преимущество в упрощении одновременного доступа, ибо изменения к лежащим ниже сырым страницам управляются отдельно от доступа к промежуточным объектам, но в результате имеют более высокие накладные расходы в оперативной памяти, так как нам приходится хранить в памяти две версии (сырые двоичные данные и внутренне присущие языку программирования) одной и той же страницы.
Третий подход заключается в предоставлении доступа к имеющемуся буферу, поддерживающему конкретный узел через некий обёртывающий объект, который материально представляет изменения в данном B- дереве как только они выполнены. Данный подход наиболее часто используется в языках с управляемой моделью памяти. Для самих изменений в имеющихся буферах поддержки применяются обёртывающие объекты.
Управление по отдельности дисковыми страницами, их кэшированными версиями и их представлениями в памяти позволяет обладать различными жизненными циклами. Например, мы можем буферировать операции вставки, обновления и удаления и согласовывать выполняемые в памяти изменения с имеющимися на диске версиями в процессе считывания.
Некоторые алгоритмы (в рамках данной книги мы будем называть их ленивыми - lazy- B- деревьями; имейте ввиду, что это не является широко принятым названием, но поскольку те варианты B- дерева, которые мы тут обсуждаем, обладают одним общим свойством - буферизацией обновлений B- дерева в промежуточных структурах вместо непосредственного применения элемента к самому дереву - мы будем пользоваться именно термином ленивые, что достаточно точно определяет такое свойство) снижают стоимости обновления B- дерева и пользуются структурами в памяти, обладающими меньшим весом, дружественным к одновременности и обновлениям, для буферизации обновлений и распространения их с некой задержкой.
Давайте рассмотрим как мы можем применять буферизацию в реализации некого ленивого B- дерева. Для этого мы можем выполнить материализацию узлов B- дерева в оперативной памяти как только подгружены страницы и применять такую структуру для хранения обновлений до тех пор, пока мы не станем го овы сбросить их.
Аналогичный подход используется в WiredTiger, теперь устанавливаемом по умолчанию механизму хранения MongoDB. Его реализация хранения строк B- дерева применяет различные форматы для страниц в памяти и на диске. Прежде чем страницы из памяти станут неизменными, им придётся пройти процесс согласования.
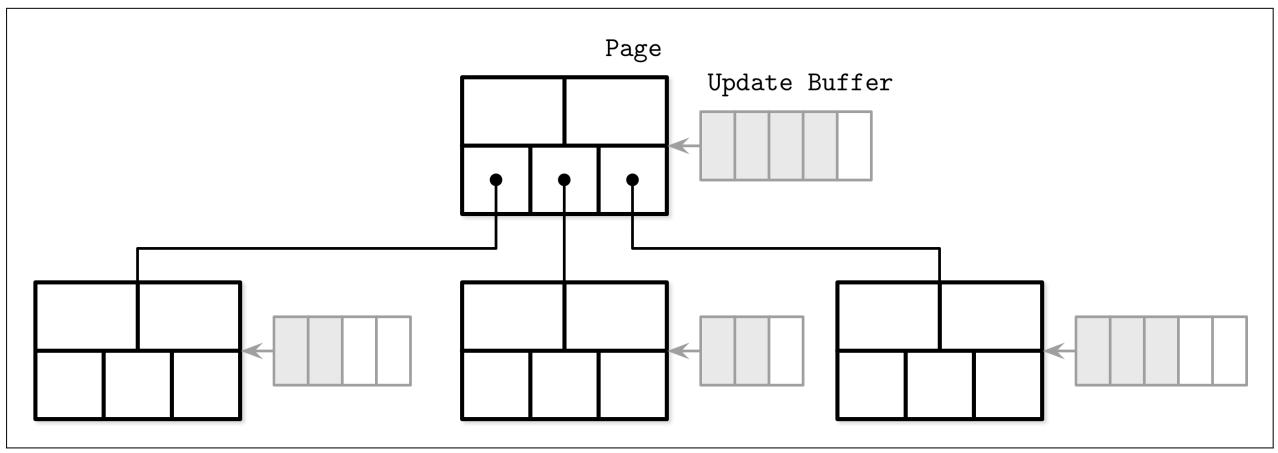
На Рисунке 6-2 вы можете видеть схематическое представление страниц WiredTiger и то как они составляют некое B- дерево. Некая чистая страница состоит лишь из какого- то индекса, изначально построенного из самого образа дисковой страницы. Обновления вначале сохраняются в имеющемся буфере обновления.
Доступ к буферам обновления выполняется считываниями: их содержимое сливается с содержимым первоначальной дисковой страницы для возврата самых последних данных. После сброса данной страницы, содержимое буфера обновления согласовывается с содержимым страницы на диске, перезаписывая первоначальную страницу. Когда размер согласуемой страницы больше максимального, она расщепляется на множество страниц. Буферы обновления реализуются при помощи списков пропусков (skiplists), которые обладают сложностью, аналогичной деревьям поиска [PAPADAKIS93], но обладают лучшим профилем одновременности [PUGH90a].
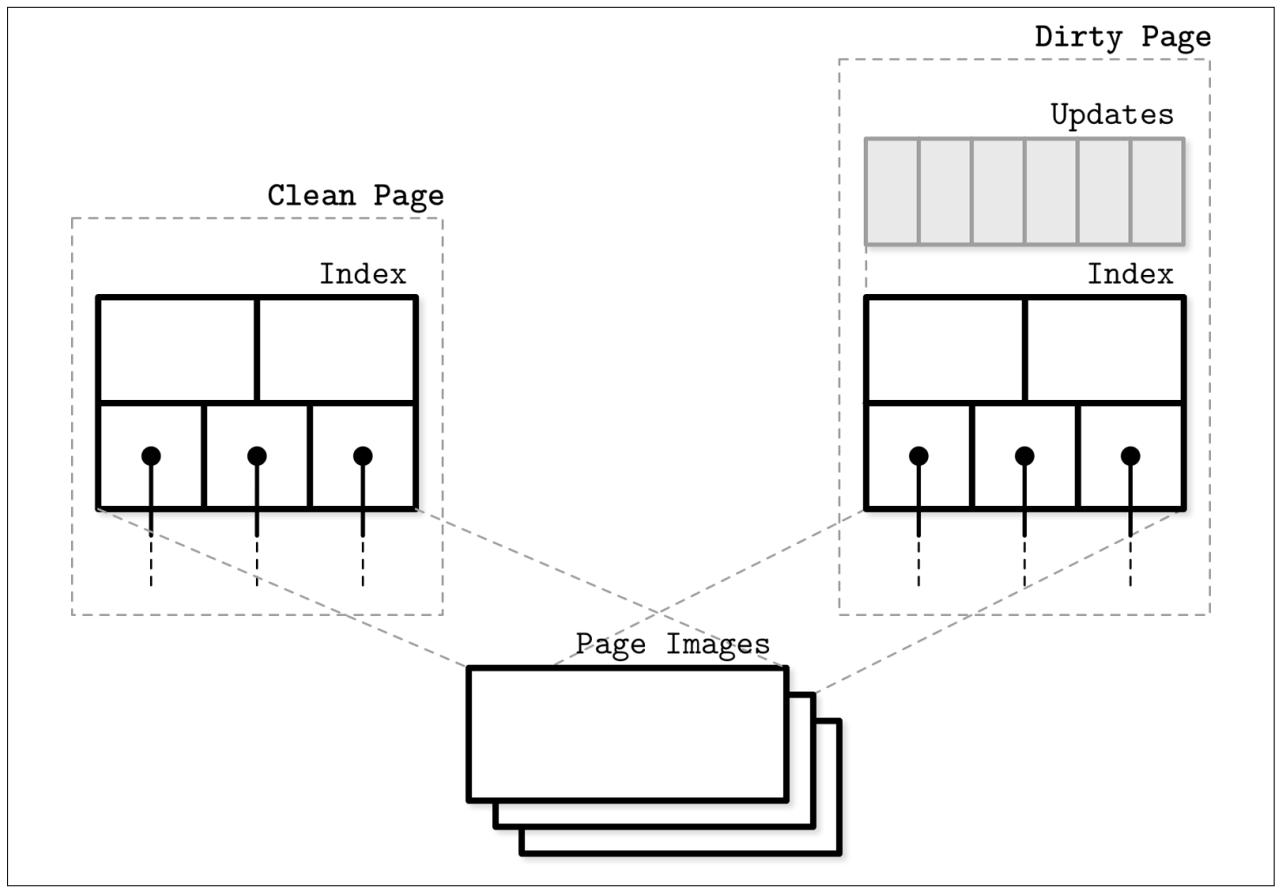
Рисунок 6-3 показывает что и чистые и испорченные страницы в WiredTiger обладают версиями в памяти и ссылкой на базовый дисковый образ. Испорченные страницы имеют дополнительно к этому некий буфер обновления.
Основное преимущество здесь состоит в том, что сами обновления страниц и структурные изменения (расщепления и слияния) выполняются определённым фоновым потоком, а процессам чтения/ записи не приходится ждать их завершения.
Вместо того чтобы буферировать обновления в индивидуальных узлах, мы можем группировать узлы в некие поддеревья и подключать какой- то буфер обновлений для выполняемых в пакете операций для каждого поддерева. Буферы обновлений в таком случае будут отслеживать все выполняемые для данного поддерева верхнего узла и его потомков действия. Такой алгоритм носит название Дерева ленивой адаптации (LA- дерева, Lazy-Adaptive Tree) [AGRAWAL09].
При вставке некой записи данных вначале в самом корневом узле буфера обновления добавляется некая новая запись. После заполнения данного буфера он опорожняется копированием и распространением всех изменений в соответствующие буферы в установленных нижних уровнях дерева. Когда сами нижние уровни также заполнены, это действие может выполняться рекурсивно, вплоть до того пока не будут достигнуты необходимые терминальные узлы.
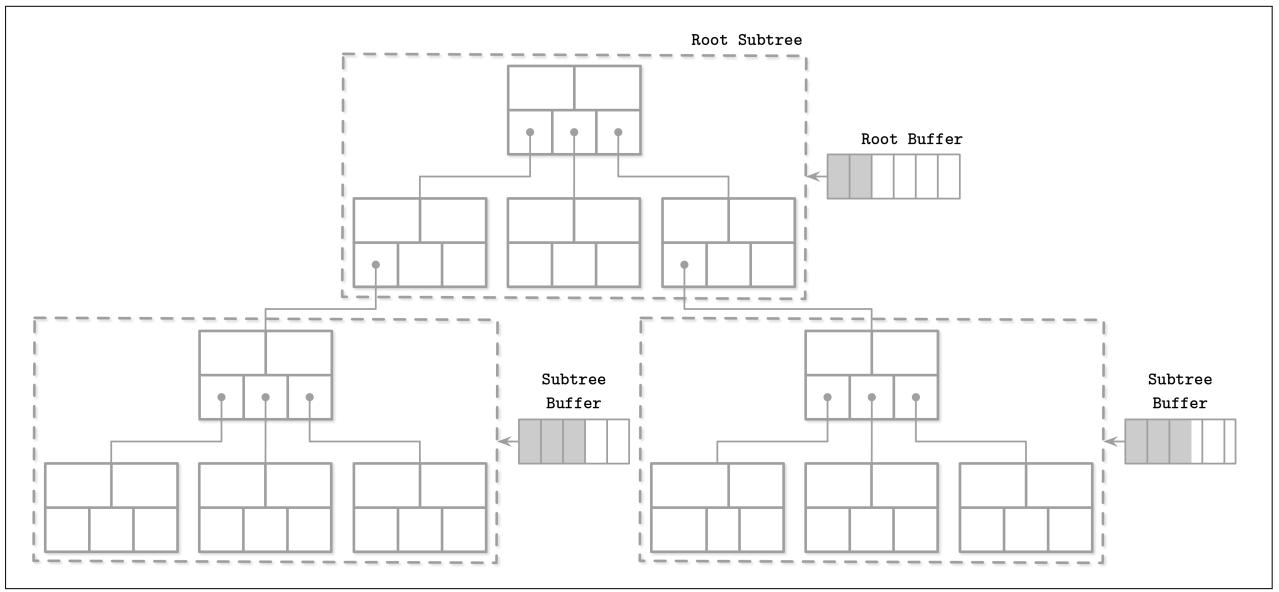
На Рисунке 6-4 вы можете наблюдать некое LA- дерево с выстроенными каскадом буферами для сгруппированных в соответствующие поддеревья узлов. Серые блоки представляют распространяемые из корневого буфера изменения.
Буферы обладают иерархическими зависимостями и выстраиваются в каскад: все обновления распространяются из буферов верхнего уровня в буферы нижнего уровня. После того как эти обновления достигают самого уровня листьев, в них пакетно выполняются операции вставки, обновления и удаления, применяя за раз все изменения к содержимому данного дерева и его структуре. Вместо выполнения последовательных обновлений на отдельных страницах, страницы могут обновляться за один проход, что требует меньшего числа доступов к диску и структурных обновлений, ибо расщепления и слияния также распространяются на более высокие уровни пакетным образом.
Все описанные здесь подходы буферизации оптимизируют время обновления дерева пакетными операциями записи, но слегка отличающимися способами. Оба алгоритма требуют дополнительного поиска в буферированных в памяти структурах, а также слияния/ согласования с ворованными дисковыми данными.
Буферизация выступает в качестве основной идеи, которая широко применяется в хранилище базы данных: она способствует избежанию множества мелких случайных записей и вместо этого выполнению одной большего размера. На жёстких дисках случайные записи медленные по причине необходимости позиционирования головок. В твердотельных накопителях нет перемещающихся частей, однако дополнительные операции ввода/ вывода вызывают некие дополнительные штрафы от сборки мусора.
Сопровождение некого B- дерева требует большого числа случайных записей - записи уровня листьев, распространяемые на их предков расщепления и слияния - но что если мы сможем избегать случайных записей, а вместе с тем и обновлений узла?
До сих пор мы обсуждали буферы обновления для индивидуальных узлов или групп узлов через создание вспомогательных буферов. Неким альтернативным подходом выступает группирование обновлений воедино имея целью различные узлы с помощью хранилища с добавлением только в конец и процессов слияния, некой идеи, которая также инспирировала деревья LSM (см. раздел Деревья LSM). Это означает, что все выполняемые нами операции записи не требуют для соответствующей записи поиска целевого узла: все обновления просто добавляются в конец. Один из примеров такого применяемого для индексации подхода носит название Дерева флэш- диска (FD- дерева, Flash Disk Tree) [LI10].
Некое FD- дерево состоит из небольшого подверженного изменениям головного дерева и множества неизменных сортированных исполнений. Этот подход ограничивает область поверхности при необходимости случайных операций ввода/ вывода имеющимся головным деревом: неким небольшим B- деревом, буферирующим такие изменения. Как только такое головное дерево заполнено, его содержимое передаётся в соответствующее неизменное исполнение (run). Когда размер вновь записываемого исполнения превосходит установленное пороговое значение, его содержимое сливается с имеющимся следующим уровнем, постепенно распространяя записи данных с верхнего на нижние уровни.
Для поддержки указателей между имеющимися уровнями FD- деревья применяют некую технологию, имеющую название
фрагментарного каскадирования (ractional cascading)
[CHAZELLE86]. Такой подход помогает снижению общей
стоимости определения места в имеющемся каскаде сортированных массивов: вы выполняете log n
шагов для обнаружения искомого элемента в самом первом массиве, но последующие поиски значительно дешевле, так как они
начинают свой поиск с самого близкого соответствия от своего предыдущего уровня.
Кратчайшие пути между имеющимися уровнями выполняются построением мостов между массивами соседних уровней для минимизации размера зазоров: элементы группируются без указателей с верхних уровней. Мосты строятся выемкой элементов с нижних уровней на более высокие, если только они там уже не имеются, и указанием того местоположения, из которого вынут этот элемент из своего массива нижнего уровня.
Поскольку [CHAZELLE86] решает задачу поиска в вычислительной геометрии, он описывает двусторонние мосты и некий алгоритм восстановления инварианта зазора, который мы не будем здесь рассматривать. Мы опишем лишь те части, которые применимы к хранилищам баз данных и, в частности, к FD- деревьям.
Вы можете создать некое соответствие от каждого элемента имеющегося массива верхнего уровня к самому ближнему элементу на
сего следующем уровне, но который не будет вызывать слишком больших накладных расходов для указателей и их сопровождения.
Если бы мы построили соответствие лишь для уже имеющихся на неком верхнем уровне элементов, мы могли бы завершить ситуацией,
при которой размер зазора между имеющимися элементами слишком велик. Для решения этой задачи мы вынимаем каждый
N-й элемент из имеющегося массива нижнего уровня на более верхний.
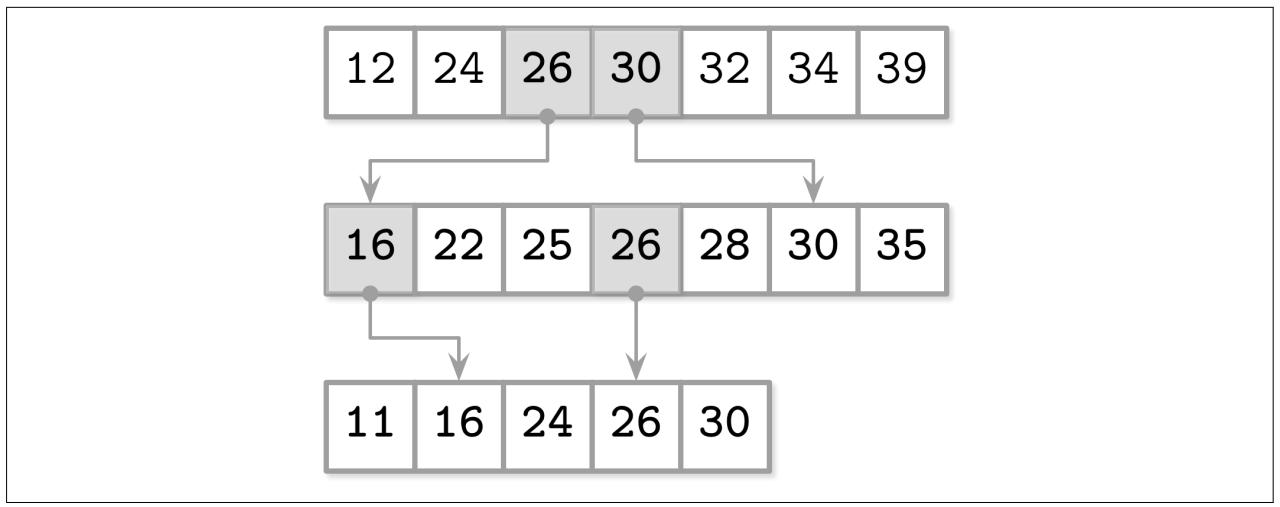
Например, когда у нас имеется множество сортированных массивов:
A1 = [12, 24, 32, 34, 39]
A2 = [22, 25, 28, 30, 35]
A3 = [11, 16, 24, 26, 30]
Мы можем сократить имеющийся зазор между элементами вынимая всякий иной элемент из имеющегося массива с более высоким индексом в массив с меньшим индексом для упрощения поисков:
A1 = [12, 24, 25, 30, 32, 34, 39]
A2 = [16, 22, 25, 26, 28, 30, 35]
A3 = [11, 16, 24, 26, 30]
Теперь мы можем воспользоваться этими вытащенными элементами для создания мостов (или как они называются в статье по FD- деревьям, препятствиях - fences): указатели от элементов верхнего уровня к их двойникам на имеющихся нижних уровнях, как это отображено на Рисунке 6-5.
Для поиска элементов во всех этих массивах, мы осуществляем некий бинарный поиск на самом верхнем уровне, при этом наше пространство поиска на его следующем уровне значительно снижается, так как теперь нам требуется перейти к примерному местоположению искомого элемента следуя по мосту. Это позволяет нам соединять множество отсортированных исполнений и снижать общие стоимости поиска в них.
Некое FD- дерево сочетает фрагментарное каскадирование с созданием логарифмически сортируемых
сортированных запусков: неизменные сортированные массивы с размерами, увеличивающимися на множитель
k, создаваемые слиянием первоначального уровня с текущим.
Самый высокий уровень исполнения (прогона, run) создаётся когда заполняется установленное головное дерево: содержимое его листьев записано на его первом уровне. Как только это головное дерево заполняется нова, его содержимое сливается с элементами его первого уровня. Эти слитые результаты в результате замещают имеющуюся старую версию такого его первого исполнения. Соответствующие прогоны нижнего уровня создаются в случае достижения размерами прогонов верхнего уровня некого порогового значения. Когда исполнение нижнего уровня уже имеется, оно замещается таким результатом слияния его содержимого с получаемым содержимым верхнего уровня. Этот процесс достаточно схож со сжатием в деревьях LSM, при котором содержимое неизменной таблицы сливается для создания таблиц большего размера.
Рисунок 6-6 отображает схематическое представление некого FD-
дерева, причём с неким головным B- деревом в его вершине, двумя логарифмическими прогонами L1
и L2 и мостами между ними.
Рисунок 6-6
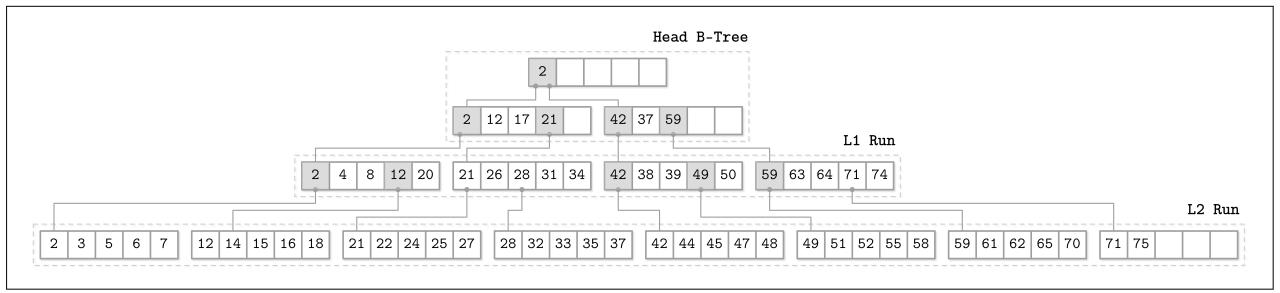
Схематичное представление FD- дерева {Прим. пер.: подробнее о построении FD- дерева в Дополнении B.}
Для того чтобы удерживать все сортированные прогоны адресуемыми, FD- деревья применяют некую адаптированную версию логарифмических прогонов, в которой головные элементы со страниц нижнего уровня распространяются как указатели на свои верхние уровни. Применяя такие указатели, снижается общая стоимость поиска на нижнем уровне, так как сам поиск уже частично выполнен на более высоком уровне и может быть продолжен с ближайшего соответствия.
Так как FD- деревья не обновляют страницы по их месту, а также может так случиться, что записи данных для одного и того же ключа присутствуют на различных уровнях, соответствующее удаление FD- деревьев работает через вставку надгробий, связанных с неким соответствующим помеченным на удаление ключом, а все записи данных для такого ключа на его нижних уровнях должны быть отвергнуты. После того как надгробия распространены по всем необходимым нижним уровням, они могут быть отброшены, так как гарантировано больше нет элементов, которые могут оставаться в тени.
Прирост записи является одной из наиболее существенных задач с реализациями обновлений по месту B- деревьев: последовательные обновления некой страницы B- дерева могут требовать обновления располагающейся на диске копии страницы при каждом обновлении. Второй значимой проблемой является приращение пространства: мы резервируем дополнительное пространство для того чтобы сделать возможными обновления. Это к тому же означает, что для каждого передаваемого полезного байта, переносящего запрошенные сведения, нам приходится передавать некие пустые байты и весь остаток этой страницы. Третья значимая проблема состоит в сложности решения задач одновременности и роботы с защёлками.
Чтобы решить все три задачи одним махом, нам придётся предпринять некий подход, полностью отличающийся от того, который мы обсуждали до сих пор. Буферирование обновлений помогает при приросте записи и пространства, но не предлагает никаких решений для проблем одновременности.
Мы можем собирать в пакет обновления к различным узлам применяя хранилище с исключительным добавлением в конец, связывать узлы воедино в цепочки и пользоваться структурами данных в памяти, которые позволяют устанавливать указатели между соответствующими узлами единственной операцией сравнить- и- обменять, делая дерево свободным от блокировок. Этот подход носит название Модного дерева (Buzzword- tree, Bw- дерева) [LEVANDOSKI14].
Некое Bw- дерево записывает какой- то базовый узел отдельно от его изменений. Изменения узлы приращений формируют цепь: некий связанный список от самых новых изменений через более старые, имея в самом конце свой базовый узел. Каждое обновление может храниться отдельно, причём без необходимости перезаписывать уже имеющийся узел на диск. Узлы приращений могут представлять вставки, обновления (которые неотличимы от вставок) или удаления.
Поскольку величины размеров базового узла и узлов приращений маловероятно выравниваются на границу страницы, стоит хранить их непрерывно, а по той причине, что ни базовый узел, ни узлы приращений не изменяются в процессе обновления (все модификации лишь вставляют некий узел в имеющийся связанный список), нам не приходится резервировать никакого дополнительного пространства.
Обладание неким узлом как логической, а не физической, сущностью это интересное изменение системы взглядов: нам не требуется предварительно выделять пространство чтобы иметь некий фиксированный размер, либо даже удерживать его в непрерывных сегментах памяти. Несомненно, у этого имеется обратная тёмная сторона: в процессе чтения требуется обходить все приращения и применять их к имеющемуся базовому узлу для перестроения реального состояния узла. Это нечто подобно тому, что делают LA- деревья (см. раздел Дерево ленивой адаптации): хранить обновления отдельно от их основной структуры и воспроизводя их при чтении.
Было бы достаточно затратным сопровождать некую дисковую структуру дерева, которая позволяла бы вставлять спереди элементы в дочерние узлы: это потребовало бы от нас постоянного обновления родительских узлов указателями на наиболее свежие приращения. Именно по этой причине узлы Bw- дерева, составляемые из некой цепи приращений и своего базового узла, обладают логическими идентификаторами и применяют некую таблицу соответствий в памяти для соответствующих идентификаторов к их местоположению на диске. Использование такого соответствия также способствует нам в избавлении от защёлок: вместо того чтобы иметь исключительное обладание на протяжении времени записи, наше Bw- дерево применяет операции сравнения- и- обмена (compare-and-swap) по физическим смещениям в своей таблице соответствий.
Рисунок 6-7 отображает образец Bw- дерева. Каждый логический узел состоит из единственного базового узла и множества связанных узлов приращений (дельта- узлов).
Рисунок 6-7
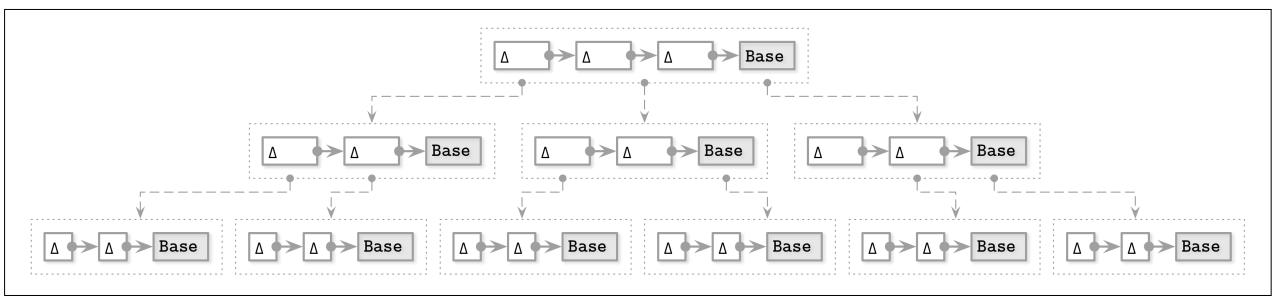
Bw- дерево. Пунктирные линии представляют связи между имеющимися узлами, разрешаемые при помощи установленной таблицы соответствий. Сплошные линии представляют реальные указатели на данные между имеющимися узлами.
Для обновления узла Bw- дерева его алгоритм выполняет следующие шаги:
-
Искомый целевой логический узел листа определяется обходом данного дерева от корня к листьям. Имеющаяся таблица соответствий содержит виртуальные связи с целевыми базовыми узлами или значение самых последних узлов приращений в установленной цепи обновлений.
-
Некий новый узел приращения создаётся с указателем на его базовый узел (или на самый последний узел приращения), найденный на шаге 1.
-
Таблица соответствия обновляется неким указателем на самый новый узел приращения, созданный в процессе шага 2.
Операция обновления на шаге 3 может осуществляться при помощи сравнения- и- перестановки (compare- and- swap), являющейся атомарной операцией, поэтому все чтения, одновременные с обновлением данного указателя, упорядочиваются либо до, либо после самой записи без блокирования как имеющихся читателей, так и самого писателя. Установленные по порядку до считывания следуют старому указателю и не видят получаемого нового узла приращения, так как он ещё не установлен. Чтения, установленные по порядку после, следуют новым указателем и наблюдают полученное обновление. Когда два потока пытаются установить некий новый узел в одном и том же логическом узле, лишь один из них может быть успешным, а другому придётся повторить свою операцию.
Bw- дерево логически структурировано как некое B- дерево, что означает, что узы всё ещё способны расти и становиться слишком большими (переполняться), либо сжиматься и становиться практически пустыми (недозаполненность) и требовать операций структурного изменения (SMO, structure modification operations), например, расщеплений и слияний. Сама семантика расщеплений и слияний здесь является аналогичной с B- деревьями (см. раздел Расщепление узла В- дерева), однако их реализация различается.
SMO расщепления стартует с консолидации имеющегося логического содержимого соответствующего расщепляемого узла, применяя приращения к его базовому узлу и создавая некую новую страницу, содержащую элементы справа от точки расщепления. После этого этот процесс проистекает в дав этапа [WANG18]:
-
Расщепление- некий специальный узел приращения добавляется в конец самого расщепляемого узла для обозначения всем читателям происходящего в данный момент расщепления. Этот узел приращения расщепления удерживает некий ключ срединной точки разделителя для лишения состоятельности записей в этом расщепляемом узле и некую связь с создаваемым новым узлом одного с ним уровня.
-
Обновление предка- В этот момент данная ситуация аналогична той, которая носит название половинного расщепления в Blink- дереве (см. раздел Деревья Blink), так как данный узел доступен через его указатель узла приращения расщепления, но ещё пока не снабжён ссылкой своего родителя и читателям приходится проходить через его старый узел и затем перемещаться по братскому указателю для достижения такого вновь создаваемого узла на том же уровне. Некий новый узел добавляется в качестве потомка общего родительского узла для того, чтобы читатели смогли напрямую достигать его вместо перенаправления через соответствующий расщеплённый узел и само расщепление завершается.
Обновление соответствующего указателя предка является оптимизацией производительности: все узлы и их элементы остаются доступными даже когда такой указатель предка и вовсе не обновляется. BW- деревья освобождены от защёлок, а потому любой поток может столкнуться с неким назавершённым SMO. Такому потоку, прежде чем продолжить, потребуется сотрудничество для подбора и завершения многоходового SMO. Последующий поток будет следовать уже установленному указателю предка и ему не придётся проходить через братский указатель.
SMO слияния работает аналогично:
-
Удаление собрата- Создаётся некий специальный узел приращения удаления и добавляется в конец надлежащего правого собрата, указывая начало данного SMO слияния и помечая своего правого собрата для удаления.
-
Слияние- Создаётся некий узел приращения слияния в соответствующем левом собрате для указания на содержимое его правого собрата и чтобы сделать его логической частью этого левого собрата.
-
Обновление предка- В этот момент к содержимому узла правого собрата доступ выполняется через узел слева. Для завершения данного процесса слияния соответствующая ссылка на его правого собрата должна быть удалена у их предка.
Одновременным SMO требуется установка в соответствующем предке некого дополнительного узла прекращения приращения во избежание одновременных расщеплений и слияний [WANG18]. Некое прекращение приращеня работает аналогично какой- то блокировке записи: только один поток способен обладать доступом на запись в некий момент времени и всякий поток, который попытается добавить в конец этого узла приращения некую новую запись бедет прерван. По завершению SMO, такое прекращение приращения может быть удалено из соответствующего предка.
В процессе расщепления узла корня растёт высота Bw- дерева. Когда имеющийся узел корня становится слишком большим, он расщепляется на два и на месте старого создаётся новый корень, причём сам старый корень и вновь созданный собрат становятся его дочерними.
Если не предпринимать каких- либо дополнительных действий, цепи приращений могут становиться произвольно длинными. Так как чтения становятся более затратными по мере того как удлиняются такие цепочки приращений, нам необходимо попытаться удерживать длину своих цепей приращения в разумных рамках. Когда они достигают некого настроенного порогового значения, мы перестраиваем данный узел сливая содержимое его базового узла со всеми прочими приращениями, собирая их в один новый базовый узел. Такой новый узел затем записывается в новом месте на диске и в установленной таблице соответствий обновляется соответствующий указатель узла чтобы отмечать его. Более подробно мы обсуждаем этот процесс в разделе Составление стека LLAMA и Mindful, поскольку за сборку мусора, объединение узлов и передислокацию отвечает лежащая в основе хранилище структурированного журнала.
После того как определённый узел объединён, его старое содержимое (сам базовый узел и все его узлы приращений) больше не имеют адресов в установленной таблице соответствий. Тем не менее, мы не можем освобождать занимаемую ими память прямо сразу, ибо некоторые из них могут использоваться в проистекающих операциях. Так как нет никаких удерживаемых читателями защёлок (читателям не приходится для доступа к данному узлу проходить сквозь некий вид барьеров или регистраций), нам необходимо найти прочие средства отслеживания живых страниц.
Для отделения потоков, которые могут сталкиваться с неким определённым узлом от тех, которые не имеют возможности его видеть, Bw- деревья пользуются технологией, имеющей название утилизации на основании эпох. Когда некие узлы и приращения удаляются из установленной таблицы соответствий благодаря объединению, которые замещают её в процессе какой- то эпохи, первоначальные узлы сохраняются до тех пор, пока не завершатся все запущенные в процессе этой или более ранних эпох читатели. После этого они могут быть безопасны собраны в мусор, так как более поздние читатели гарантировано никогда не должны видеть эти узлы, так как они больше не имеют адресов на тот момент, когда запускаются читатели.
Такое Bw- дерево является неким занимательным вариантов B- дерева, выполняющим улучшения для ряда важным сторон: прироста числа записей, не блокируемого доступа и дружелюбия кэшированию. Некая видоизменённая версия была реализована в Sled, экспериментальном механизме хранения. CMU Database Group разработала некую версию Bw- дерева в оперативной памяти под названием OpenBw-Tree и выпустила некое практическое руководство реализации [WANG18].
В этой главе мы всего лишь прикоснулись к понятиям верхнего уровня Bw- дерева, относящихся к B- деревьям, и мы продолжим их обсуждение в разделе Составление стека LLAMA и Mindful, включая рассмотрение лежащего в основе хранилища структурированных журналов.
Размер блока, размер узла, выравнивание линий кэша и прочие параметры настройки влияют на производительность B- дерева. Некий новый класс структур данных с названием не замечающих кэш структур (cache-oblivious structures) [DEMAINE02] предоставляют асимптотически оптимальную производительность вне зависимости от лежащей в основе иерархии памяти и потребности в настройке этих параметров. Это означает, что такой алгоритм не требует знания размеров имеющихся строк кэширования, блоков файловой системы и страниц дисков. Не замечающие кэширование структуры разработаны для надлежащей работы без изменений во множестве машин с различными настройками.
До сих пор мы в основном рассматривали B- деревья с двухуровневой иерархией памяти (за исключением LMDB, описанных в разделе Копирование записью). Узлы B- дерева хранятся в дисковых страницах, а для возможности действенного доступа к ним в оперативной памяти применяется устанавливаемый кэш страниц.
Такими двумя уровнями иерархии выступают кэш страниц (который является более быстрым, но ограничен в размере) и диск (значительно более медленный, но обладающий большей ёмкостью) [AGGARWAL88]. В этом случае у нас имеются лишь два параметра, что упрощает проектирование алгоритмов, ибо нам приходится иметь дело лишь с двумя модулями кода, особенными для уровня, которые и заботятся обо всех относящихся к такому уровню деталях.
Чам диск разбивается на части в блоки и обмен данными между диском и кэшем выполняется блоками: даже когда самому алгоритму приходится определять место отдельного элемента внутри блока, должен быть загружен весь блок целиком. Этот подход является осведомлённым о кэшировании.
при разработке критичного к производительности программного обеспечения, мы зачастую программируем более сложную модель, учитывая кэши ЦПУ, а порой даже иерархию дисков (например, горячее/ холодное хранение, или выстраивание иерархий HDD/ SSD/ NVMe, а также стадий переключения данных с одного уровня на другой). В большинстве случаев такие усилия сложно обобщать. В разделе Сопоставление DBMS в памяти и основанных на дисках мы обсудили тот факт, что доступ к диску на несколько порядков медленнее доступа к основной памяти, что имеет мотивацию реализующих базу данных в оптимизации данной разницы.
Не учитывающие кэширование алгоритмы позволяют рассуждать о структурах данных в терминах двухуровневой модели памяти, предоставляя при этом основные преимущества модели иерархии со множеством уровней. Такой подход позволяет не иметь платформо- зависимых параметров и при этом обеспечивать общее число обменов между имеющимися двумя уровнями представленной иерархии в рамках постоянного множителя. Когда такая структура данных оптимизирована для оптимального выполнения в любых двух уровнях иерархии памяти, она также оптимально рабоатает для соответствующих двух смежных уровней иерархии. Это достигается при работе в наивысшем уровне кэширования с максимально возможной степенью.
Не замечающие кэширование B- деревья состоят из некого статического B- дерева и структуры упакованного массива
[BENDER05]. Статическое B- дерево строится с применением
установленной схемы ван Эмде Боаса. Она расщепляет всё дерево на на своём среднем уровне
имеющихся граней. Далее каждое поддерево рекурсивно расщепляется до меньшего размера, имея в результате поддеревья с размером
в sqr(N). Ключевая мысль этой схемы состоит в том, что любое рекурсивное дерево
хранится в каком- то непрерывном блоке памяти.
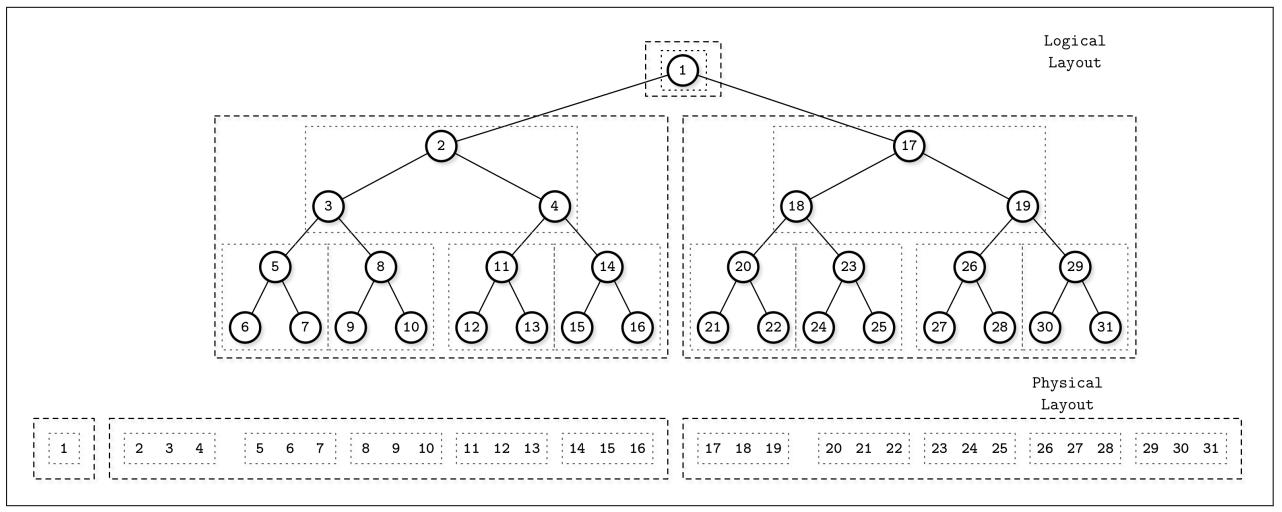
На Рисунке 6-8 вы можете видеть некий образец схемы ван Эмде Боаса. Логически сгруппированные совместно узлы помещаются поблизости друг от друга. В его верхней части вы можете отслеживать некую логическую схему представления (то есть как узлы формируют некое дерево), а снизу вы можете наблюдать как узлы дерева размечаются в памяти и на диске.
Чтобы сделать эту структуру данных динамичной (то есть разрешить вставки, обновления и удаления), не замечающие кэширования деревья применяют некую структуру данных упакованного массива, которая пользуется непрерывными сегментами памяти для хранения элементов, но содержит зазоры, зарезервированные для последующих вставок элементов. Зазоры разносятся в пространстве на основании порогового значения плотности. Рисунок 6-9 демонстрирует структуру упакованного массива, в которой элементы снабжены пробелами для создания зазоров.
Данный подход позволяет вставлять элементы в имеющееся дерево с меньшим числом перемещений. Элементы должны перемещаться просто для создания некого зазора для подлежащего вставке нового элемента, если такой зазор уже не представлен. Когда такой упакованный массив превращается в слишком плотный или редко заселённым, его структура подлежит перестроению для роста или сжатия соответствующего массива.
Само статическое дерево применяется в качестве индексного для своего упакованного массива нижнего уровня и обязано обновляться в соответствии с перемещениями элементов для указания на верные элементы нижнего уровня.
Это занимательный подход и его идеи можно применять при построении действенных реализаций B- дерева. Он позволяет конструировать дисковые структуры теми способами, которые очень сходи с тем, как они конструируются в основной памяти. Тем не менее, на момент написания книги, мне пока не встречались никакие не академические реализации не замечающих кэширования B- деревьев.
Возможная причина этого состоит в том предположении, что при абстрагировании от загрузке в кэш и записи загруженных данных обратно в блоки, подгрузка страниц и их вытеснение по- прежнему отрицательно влияют на получаемый результат. Другой возможной причиной является то, что в терминах блочного обмена, степень сложности не замечающих кэширования B- деревьев та же самая что и у их осведомлённых о кэшировании противников. Это может измениться когда более распространёнными станут более эффективные устройства хранения с энергонезависимой байт- адресуемой памятью.
Изначальная архитектура B- дерева имеет ряд недостатков, которые могут приемлимо работать на шпиндельных дисках, но становиться менее эффективными при применении SSD. B- деревья обладают высокой степенью прироста записи (вызываемого перезаписью страниц) и высокими накладными расходами пространства, так как B- деревьям приходится резервировать пространство в узлах для последующих записей.
Прирост записей может быть снижен при помощи буферирования. Ленивые B- деревья, такие как WiredTiger и LA- деревья, подключают буферы памяти к индивидуальным узлам или группам узлов для снижения общего числа необходимых операций ввода/ вывода буферируя последовательные обновления в страницах в памяти.
Для снижения прироста пространства, FD- деревья пользуются неизменностью: записи данных хранятся в неизменных сортированных прогонах, а размер изменяемого B- дерева ограничен.
Bw- деревья также решают задачу прироста пространства при помощи не изменяемости. Узлы B- дерева и обновления в них хранятся в раздельных местах на диске и удерживаются в установленном хранилище структурированного журнала. Прирост записи снижается в сравнении с изначальной архитектурой B- дерева, так как согласование содержимого, относящегося к отдельному логическому узлу относительно редко. Bw- деревья не нуждаются в защёлках для защиты страниц от одновременного доступа, поскольку виртуальные указатели между имеющимися логическими узлами хранятся в памяти.
![[Замечание]](/common/images/admon/note.png) | Последующее чтение |
|---|---|
|
Если вы желаете узнать больше относительно упоминавшихся в этой главе понятий, вы можете ссылаться на следующие источники:
|