Глава 2. Основы B- деревьев
Содержание
В своей предыдущей главе мы разделили структуры хранения на две группы: изменяемые и неизменные и указали на неизменность как одно из центральных понятий, оказывающих влияние на их проектирование и реализацию. Большинство изменяемых структур применяют некий механизм обновления на месте. В процессе операций вставки, удаления или обновления записи данных обновляются непосредственно по их месту в самом целевом файле.
Механизмы хранения часто допускают множество версий одной и той же записи данных для её представления в самой базе данных: например, при использовании контроля одновременности множества версий (см. Управление одновременностью множества версий) или при организации перекидных страниц (см. Перекидные страницы). С целью упрощения на данный момент мы предположим, что каждый ключ связан лишь с одной записью данных, которая имеет некое уникальное место.
Одной из наиболее популярных структур является B- дерево {произносится: Бэ- дерево}. Многие системы баз данных с открытым исходным кодом являются основанными на B- деревьях и на протяжении многих лет они доказали охват основной массы вариантов использования.
B- деревья не являются недавним изобретением: они были введены Рудольфом Байером и Эдвардом М. макКрейтом ещё в 1971 и с годами обрели популярность. К 1979 году имелось уже достаточно много вариантов B- деревьев. Дуглас Коммер собрал и систематизировал некоторые из них [COMER79].
Прежде чем мы окунёмся в B-деревья, давайте вначале обсудим зачем нам стоит рассматривать альтернативы традиционным деревьям поиска, таким как, например, двоичные деревья поиска, деревья 2-3 и деревья AVL [KNUTH98]. Для этого давайте напомним что такое деревья двоичного поиска.
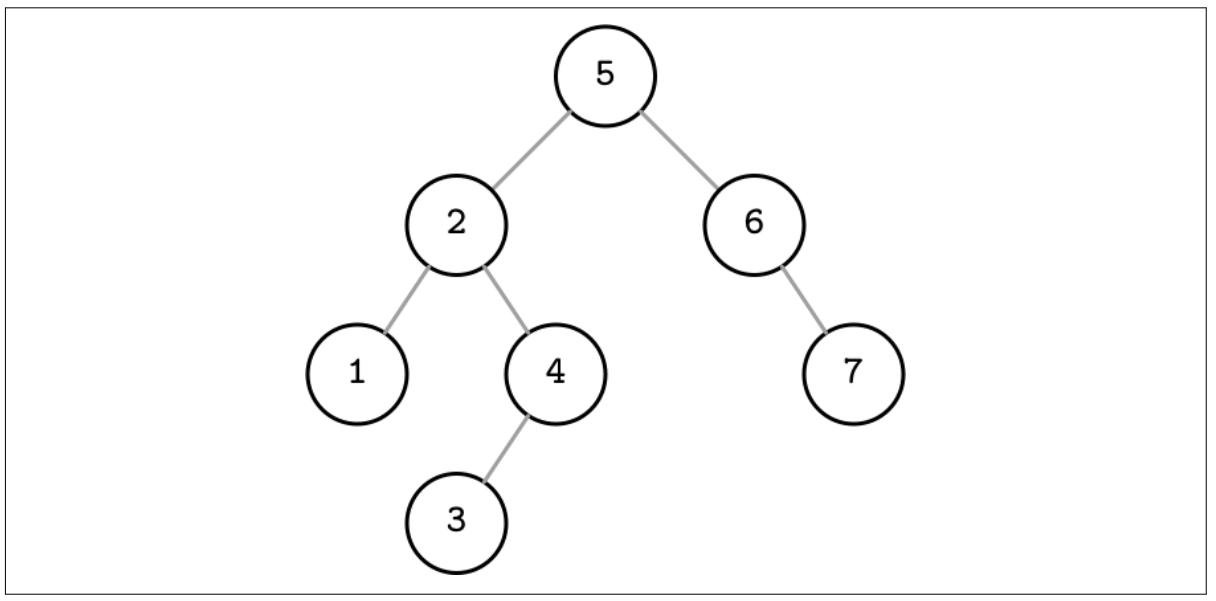
Дерево двоичного поиска (BST, binary search tree) это сортированная в памяти структура данных, используемая для действенного поиска ключ- значение. BST состоит из множества узлов. Каждый узел дерева представлен неким ключом, связанным с этим ключом значением и двумя дочерними указателями (отсюда и название двоичного). BST стартует с одного узла, имеющего название корневого узла. В определённом дереве может иметься лишь один корень. Рисунок 2-1 отображает некий пример дерева двоичного поиска.
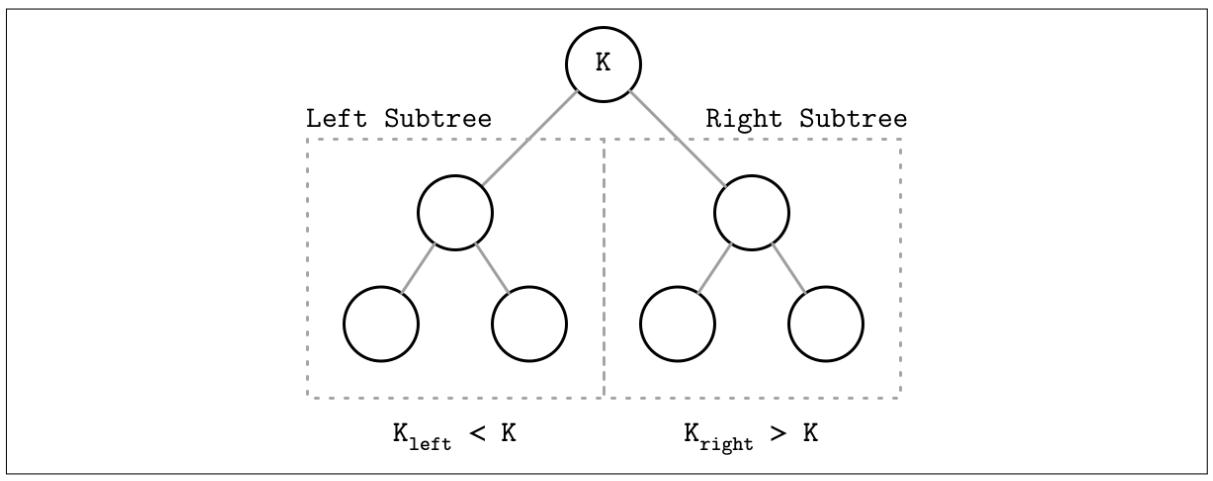
Каждый узел расщепляет общее пространство поиска на левое и правое поддеревья, как это показывает Рисунок 2-2: некий ключ узла больше чем все хранящиеся в левом поддереве ключи и меньше чем все ключи хранящиеся в его правом поддереве [DECANDIA07].
Следуя за левыми указателями от самого корня данного дерева вниз до уровня листьев (того уровня, на котором узлы не имеют детей) находятся узел, содержащий наименьшее значение ключа в дереве, а также связанное с ним значение. Аналогично, следуя по правым указателям определяется местонахождение узла, содержащего самое большое значение ключа внутри этого дерева и связанного с ним значения. Допускается хранение значений во всех узлах этого дерева. Поиски начинаются с корневого узла и могут завершаться до достижения самого нижнего уровня данного дерева, когда искомый ключ был обнаружен на более высоком уровне.
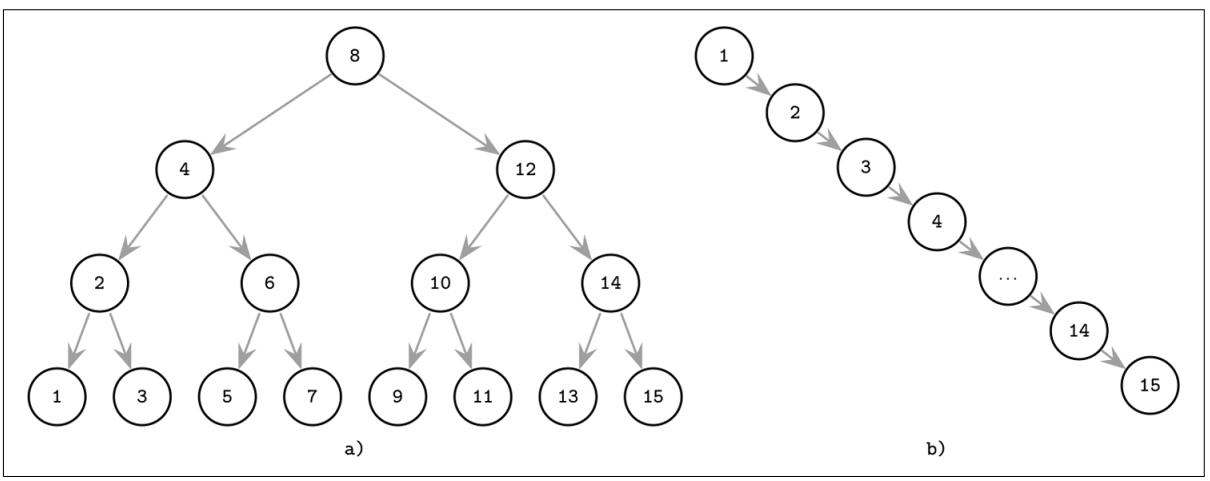
Операция вставки не следует никакому определённому шаблону и вставка элемента может приводить к такой ситуации, когда ваше дерево не сбалансировано (т.е. одна из его ветвей длиннее всех прочих). Самый худший сценарий показан на Рисунке 2-3 (b), при котором мы в конечном счёте получаем патологическое дерево, которое больше похоже на некий связанный список и вместо логарифмической сложности мы получаем линейную, как это проиллюстрировано Рисунке 2-3 (a).
Данный пример возможно слегка преувеличивает имеющуюся проблему, однако иллюстрирует зачем нашему дереву требуется сбалансированность: даже хотя это и нечто маловероятное, что все имеющиеся элементы в конечном итоге оказываются в одной стороне нашего дерева, по крайней мере часть из них несомненно будут такими, что значительно замедлит поиск вниз по дереву.
Сбалансированное дерево определяется как имеющее высоту в
log2 N, где N это общее
число элементов данного дерева и значение разницы в высоте между любыми двумя поддеревьями не превышает единицы
[KNUTH98]. (Данное требование накладывается деревьями AVL
и некими прочими структурами данных. В более общем случае деревья двоичного поиска удерживают численную разницу ы
высотах между поддеревьями в пределах небольшого постоянного фактора.) Без сбалансированности мы утрачиваем преимущества
производительности своего двоичного поиска в структуре дерева и допускаем порядку вставок и удалений определять
форму дерева.
В сбалансированном дереве, следуя за указателем влево или вправо, пространство поиска в среднем сокращается вдвое,
а потому сложность поиска является логарифмической: O(log2 N). Когда
наше дерево не сбалансировано, в наихудшем случае сложность достигает O(N), так
как мы можем получить в конечном счёте ситуацию, при которой все элементы выстраиваются по одну сторону данного
дерева.
Вместо добавления новых элементов в одну из ветвей своего дерева и удлиняя её, в то время как прочие остаются пустыми (как это показано на Рисунке 2-3 (b)), хорошее дерево является сбалансированным после каждой операции. Балансировка осуществляется за счёт реорганизации узлов таким образом, чтобы минимизировать высоту дерева и сохранять значение числа узлов с каждой стороны в границах.
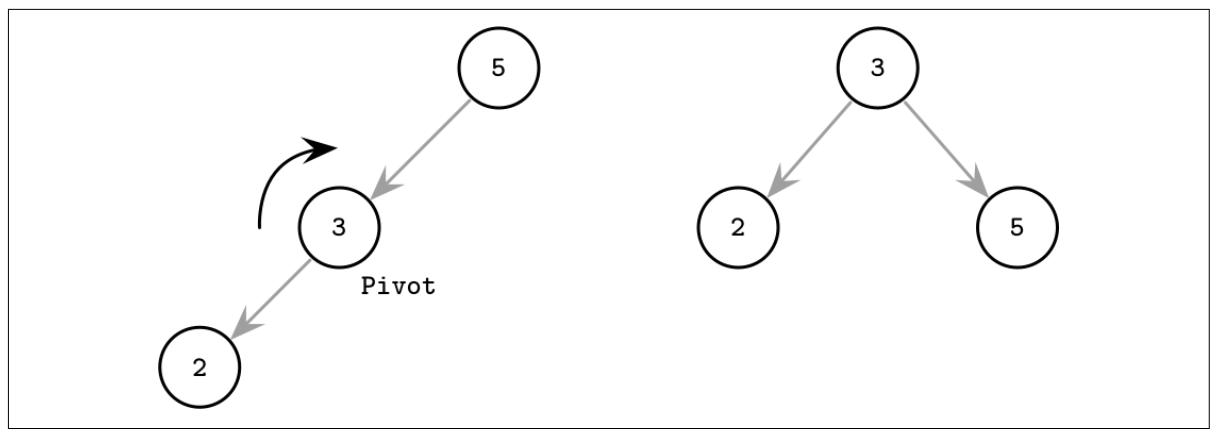
Один из способов сохранения своего дерева сбалансированным является выполнение шага разворота после добавления или удаления узлов. Когда операция оставляет некую ветвь несбалансированной (два последующих узла в этой ветви обладают лишь одним потомком), мы можем развернуть узлы вокруг их середины. В показанном на Рисунке 2-4 примере, в процессе разворота нашего среднего узла (3), имеющего названия оси поворота (rotation pivot), он передвигается на один уровень вверх, а его родитель становится его правым потомком
Как уже упоминалось ранее, несбалансированные деревья имеют наихудшую сложность в O(N).
Сбалансированные деревья дают нам в среднем O(log2 N). В то же самое
время, вследствие низкого ветвления (fanout, ветвление это значение максимально
допустимого для узла числа потомков), нам приходится достаточно часто выполнять балансировку, перемещение узлов и
обновление указателей. Рост стоимости сопровождения делает BST непрактичным для дисковых структур данных
[NIEVERGELT74].
Если мы хотим поддерживать на диске некий BST, мы сталкиваемся с рядом проблем. Одна из задач состоит в локальности: так как элементы добавляются случайным образом, нет никакой гарантии того, что вновь создаваемый узел записывается поблизости от своего предка, что означает, что указатели дочернего узла могут расширяться по нескольким страницам диска. До некоторой степени мы можем улучшить это положение, изменяя схему своего дерева и применяя страничные двоичные деревья (см. Страничные двоичные деревья).
Другая задача, тесно связанная со значением стоимости последующих уникальных указателей это высота дерева.
Так как двоичные деревья имеют ветвление равное всего лишь двум, высота равна двоичному логарифму от общего числа всех
элементов в данном дереве и нам приходится выполнять O(log2 N)
поисков для определения места элемента и вследствие этого, выполнение того же самого числа обменов с дисками. 2-3-
Деревья и прочие деревья с низким ветвлением имеют аналогичное ограничение: в то время как они полезны в качестве
размещаемых в памяти структур, малый размер узла делает их непрактичными для внешних хранилищ
[COMER79].
Безыскусная дисковая реализация BST потребует того же самого числа поисков на диске, сколько имеется сравнений, так как нет никакой концепции локальности. Это заставляет нас следовать поиском некой структуры данных, которая будет демонстрировать это свойство.
Принимая во внимание эти факторы, версия того дерева, которое луше всего подходило бы для реализации на диске, должны выставлять такие свойства:
-
Высокой степенью ветвления для улучшения локализации значений соседних ключей.
-
Низкой высоты для снижения общего числа поисков в процессе просмотра- обхода.
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Ветвление и высота имеют обратную корреляцию: чем выше значение ветвления, тем ниже высота. Когда ветвление высокое, каждый узел может сохранять больше потомков, снижая общее число узлов и, по этой причине, снижая высоту. |
В общих чертах мы уже обсуждали хранилища в памяти и на диске (см. Главе 2,). Мы можем провести то же самое отличие для специальных структур данных: некоторые лучше приспособлены для использования на диске, а некоторые лучше в памяти.
Как мы уже обсуждали, не все удовлетворяющие требованиям пространства и сложности структуры данных способны. Применяемые в базах данных структуры данных должны быть приспособлены для учёта постоянных средних ограничений.
Дисковые структуры данных часто используются когда имеющиеся объёмы данных настолько велики, что удерживать весь набор данных в памяти невозможно или невыполнимо. Только часть данных может быть кэширована в памяти в любой момент времени, а все остальные приходится хранить на диске неким образом, который делает возможным действенный доступ к ним.
Большинство традиционных алгоритмов были разработаны когда шпиндельные диски были наиболее распространённым постоянным носителем хранения, что существенно повлияло на их проектирование. Позднее, новые разработки, такие как флеш устройства, вдохновили новые алгоритмы и изменения в уже имеющихся, эксплуатируя появившиеся возможности такого нового оборудования. В эти дни нарождаются новые типы структур данных, которые оптимизированы для работы с энергонезависимыми хранилищами с байтовой адресацией (например, [XIA17], [KANNAN18]).
На шпиндельных дисках, позиционирование (seek) увеличивает стоимость произвольных считываний, так как они нуждаются во вращении диска и механическом перемещении головок в положение самих головок чтения/ записи в желаемое положение. Однако, после выполнения этой затратной части, чтение или запись непрерывных байт (то есть последовательные действия) относительно недороги.
Самым малым элементом обмена некого шпиндельного устройства является сектор, а потому когда выполняется некая операция, должен быть считан или записан по крайней мере весь сектор целиком. Размер сектора обычно находится в диапазоне от 512 байт до 4 кБ. {Прим. пер.: подробнее о проблемах размера сектора на диске в Обзоре технологии Расширенного формата жёстких дисков Ильи Крутова, IBM.}.
Позиционирование головок это наиболее затратная часть операций HDD. Это одна из тех причин, которую мы часто слышим как получаемые положительные эффекты последовательного ввода/ вывода: чтения и записи непрерывных сегментов диска.
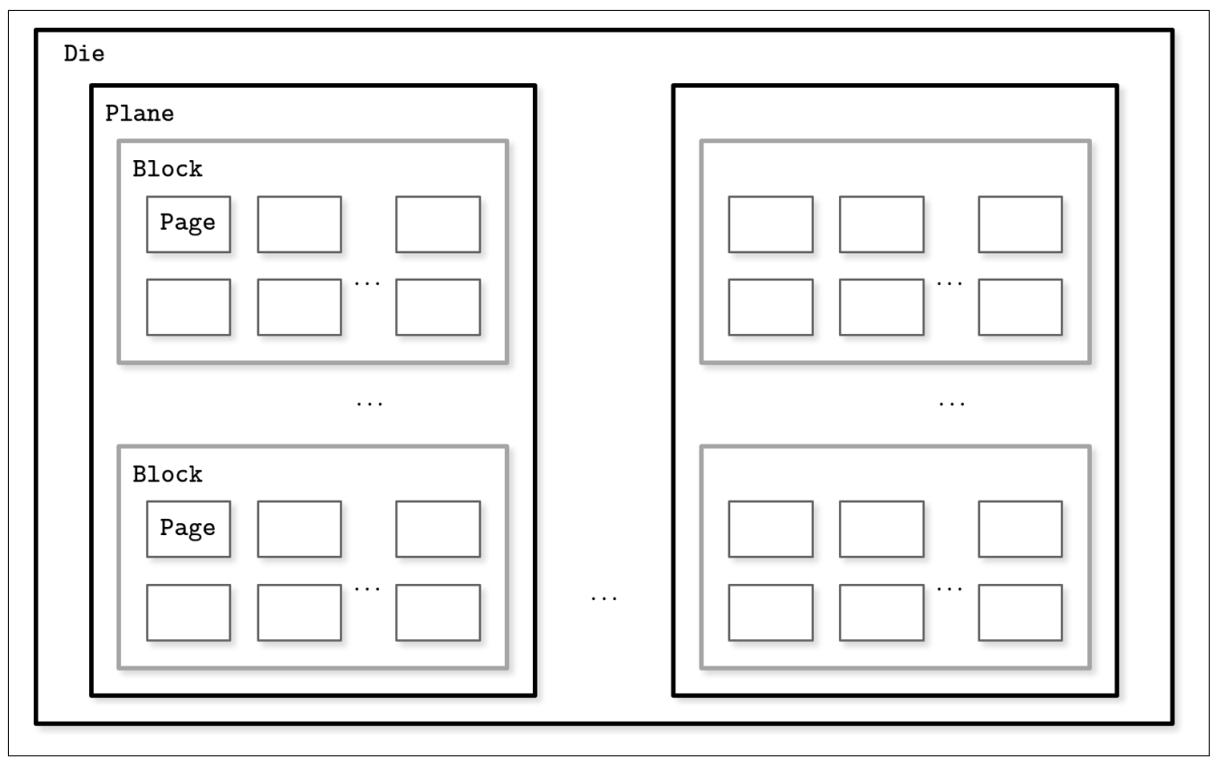
Твердотельные устройства (SSD) не имеют перемещающихся частей: нет никаких вращающихся дисков или головок, которые приходится позиционировать для такого чтения. Типичный SSD строится из ячеек памяти (memory cells), соединённых в цепочки (струны, strings, обычно от 32 до 64 на цепочку), цепочки комбинируются в массивы, массивы собираются в страницы, а страницы сочетаются в блоки [LARRIVEE15].
В зависимости от конкретно применяемой технологии, ячейка может содержать один или множество бит данных. Страницы варьируются в размере для устройств, но обычно их размеры находятся в диапазоне от 2 до 16 кБ. Блоки обычно содержат от 64 до 512 страниц. Блоки организованы в плоскости (planes) и, наконец, плоскости помещаются в чип (кристалл, die). SSD могут иметь один или более чипов. Рисунок 2-5 отображает данную иерархию.
Наименьший элемент, который можно записать (запрограммировать) или считать, это страница. Однако мы можем вносить изменения только в имеющиеся пустыми элементы памяти (то есть в те, которые были стёрты перед такой записью). Самым наименьшим логическим элементом удаления является не страница, а блок, который содержит множество страниц, и именно поэтому это часто имеет название удаление блока. Страницы некого пустого блока приходится записывать последовательно.
Основная часть некого контроллера флеш памяти, отвечающая за соответствие идентификаторов страниц их физическим положениям, отслеживание пустых, записанных и отвергнутых страниц, имеет название FTL (Flash Translation Layer, см. Слой трансляции флеш- устройства для получения дополнительных сведений об FTL). Он также отвечает за сборку мусора, в процессе которого FTL выискивает блоки, которые он способен безопасно удалить. Некоторые блоки всё ещё могут содержать живые страницы. В таком случае он перемещает живые страницы с таких блоков в новые расположения и устанавливает новое соответствие идентификатора страницы для указания сюда. После этого он уничтожает такие неиспользуемые блоки, делая их доступными для записей.
Поскольку в обоих типах устройств (HDD и SSD) мы выполняем адресацию к фрагментам памяти вместо индивидуальных байт (то есть выполняем доступ к блоку данных целиком), большинство операционных систем имеют некую абстракцию блочного устройства [CESATI05]. Она скрывает внутреннюю структуру диска и внутренним образом буферирует операции ввода/ вывода, а потому когда мы считываем отдельное слово из блочного устройства, считывается все содержимое целого блока. Такое обязательство мы не можем игнорировать и всегда обязаны учитывать при работе с располагающимися на диске структурами данных.
В SSD мы не выделяем строго сопоставление произвольного и последовательного ввода/ вывода, как это имеет место для HDD, так как различие в задержках между произвольными и последовательными чтениями не велико. Всё ещё имеется различие, вызываемое упреждением, считыванием непрерывных страниц и внутренней параллельностью [GOOSSAERT14].
Даже несмотря на то, что сборка мусора является обычно некой выполняемой в фоновом режиме операцией, её эффект может оказывать отрицательное воздействие на производительность записи, в особенности в случаях произвльных и неупорядоченных рабочих нагрузок записи.
Запись только полных блоков и комбинирование последовательных записей в одном и том же блоке может способствовать снижению общего числа требуемых операций ввода/ вывода. В последующих главах мы обсудим буферизацию и неизменность как пути достижения этого.
Помимо стоимости дискового доступа самого по себе, самым основным ограничением и условием проектирования для построения действенных дисковых структур выступает тот факт, что наименьшим элементом дисковой операции является некий блок. Для следования по указателю в конкретному месту внутри такого блока,нам приходится выполнять выборку всего блока целиком. Раз уж нам приходится это делать, мы можем изменять саму схему такой структуры данных для получения от этого преимуществ.
На протяжении этой главы мы уже упоминали несколько раз указатели, однако это слово имеет слегка отличную семантику для дисковых структур. На диске в большинстве случаев мы управляем своей схемой данных вручную (пока мы, например, не применяем файлы соответствия памяти). Это всё ещё схоже с обычными операциями с указателями, но нам приходится вычислять необходимые адреса целевого указателя и следовать таким указателям в явном виде.
В большинстве случаев дисковые смещения предварительно вычисляются (в случаях, когда такой указатель уже записан на диск перед тем как данная часть указывает на него) или кэшируется в памяти пока они не будут сброшены на этот диск. Создание длинных цепочек зависимостей в дисковых структурах значительно увеличивайте код и сложность структуры, поэтому более предпочтительно сохранять общее число указателей и их диапазонов в минимальном значении.
Суммируя, дисковые структуры проектируются с сохранением в памяти их специфических особенностей хранения и обычно оптимизируются под меньшее число доступов к диску. Мы можем делать это улучшая локальность, оптимизируя имеющееся внутреннее представление данной структуры и снижая общее число указателей вне страницы.
В Деревья двоичного поиска мы пришли к заключению, что высокая степень ветвления и низкая высота являются желательными свойствами для оптимальной дисковой структуры. Мы также только что обсудили проистекающие от указателей дополнительные накладные расходы в пространстве и накладные расходы сопровождения за счёт установления повторного соответствия этих указателей в результате балансировки. B- деревья сочетают эти идей: увеличивают число ветвлений узла и снижают высоту дерева, общее число указателей на узлы, а также значение частоты операций балансировки.
![[Замечание]](/common/images/admon/note.png) | Страничные двоичные деревья |
|---|---|
|
Выстраивание схемы двоичного дерева путём группирования узлов на страницы, как это показано на Рисунке 2-6, улучшает положение дел с локальностью. Для поиска следующего узла, необходимо лишь следовать некому указателю в уже выбранной странице. Однако, всё ещё имеются некие накладные расходы, проистекающие из самих узлов и указателей между ними. Размещение такой структуры на диске и её последующее сопровождение является нетривиальным предприятием, в особенности когда ключи и значения не сортированы предварительно и добавляются произвольным образом. Балансировка требует реорганизации страницы, что в свою очередь вызывает обновление указателей. |
Мы отважней чем пчёлы, и ух... длиннее чем деревья...
Винни Пух
B- деревья можно представлять себе как некое бескрайнее помещение каталога в библиотеке: вначале вам требуется найти правильный шкаф, затем верную полку в этом шкафу, после этого правильный выдвижной ящик на полке, а затем пролистать все карточки в этом ящике чтобы отыскать то что вы ищете. Аналогично, некое B-дерево выстаивает иерархию, котрая быстро помогает в навигации и определении местоположения искомых элементов.
Как мы уже обсуждали в Деревьях двоичного поиска, B- деревья строятся поверх основания сбалансированных деревьев поиска и отличаются тем, что имеют более высокий порядок ветвления (обладают большим числом дочерних узлов) и меньшей высотой.
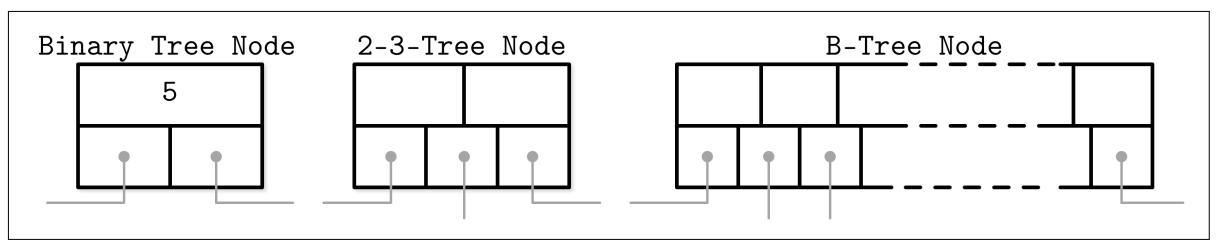
В большинстве литературных источников узлы двоичных деревьев рисуются окружностями. Так как каждый узел отвечает только за один ключ и расщепляет свой диапазон на две части, такого уровня подробности достаточно и он интуитивно ясен. В то же самое время, узлы B- дерева часто изображаются прямоугольниками, а блоки указателей также отражаются в явном виде для выделения имеющейся взаимосвязи между дочерними узлами и ключами разделителя. Рисунок 2-7 показывает двоичное дерево, дерево 2-3 и узлы B- дерева бок о бок, что помогает понять сходства и различия между ними.
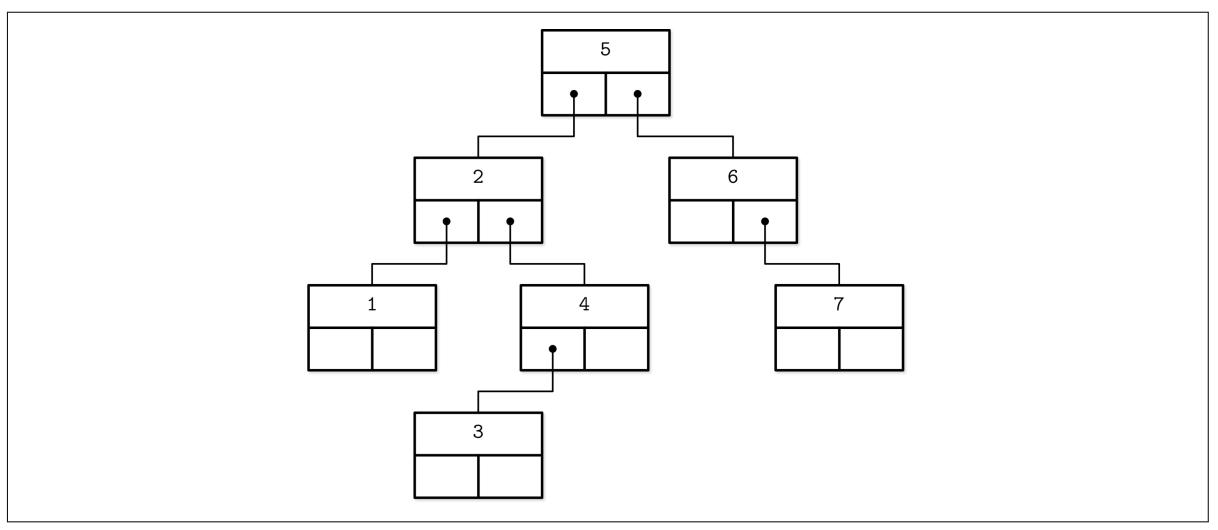
Ничто не мешает нам перерисовать двоичное дерево точно так же. Обе структуры имеют аналогичную семантику следования указателям, а отличия начинают проявляться в том как сопровождается их балансировка. Рисунок 2-8 показывает это наводит на мысль о сходстве между BST и B- деревьями: в обоих случаях ключи расщепляют само дерево на поддеревья и применяются для навигации по самом у дереву и поиска искомых ключей. Вы можете сравнить его с Рисунком 2-1.
B- деревья сортированы: ключи внутри самого узла B- дерева находятся в порядке
сортировки. Благодаря этому, для определения места некого искомого ключа мы можем применять некий алгоритм, подобный
двоичному поиску. Это также подразумевает, что поиск по B- деревьям обладает логарифмической сложностью. Например,
поиск искомого ключа среди 4 миллиардов (4 × 109) элементов занимает
около 32 сравнений (см. Сложность поиска в В- деревьях для
дополнительных сведений по этому вопросу). Когда нам приходится выполнять дисковое позиционирование для каждого из
таких сравнений, это значительно замедлило бы нас, но так как узлы B- дерева хранят десятки и даже сотни элементов,
нам всего лишь придётся выполнят по одному позиционированию диска для прыжка на следующий уровень. Позднее в этой главе
мы обсудим алгоритм поиска более подробно.
При помощи B- деревьев мы можем действенно выполнять как запросы указания, так
и запросы диапазона. Запросы указания, выражаемые в большинстве языков запросов
знаком предиката равенства (=) определяют место единственного элемента.
С другой стороны, запросы диапазона, выражаемые символами предикатов сравнения (<,
>, ≤ и ≥)
используются для запроса множества элементов данных в распоряжении.
B- состоят из множества узлов. Каждый узел содержит до N ключей и
N + 1 указателей на его дочерние узлы. Эти узлы логически разбиваются на три
группы:
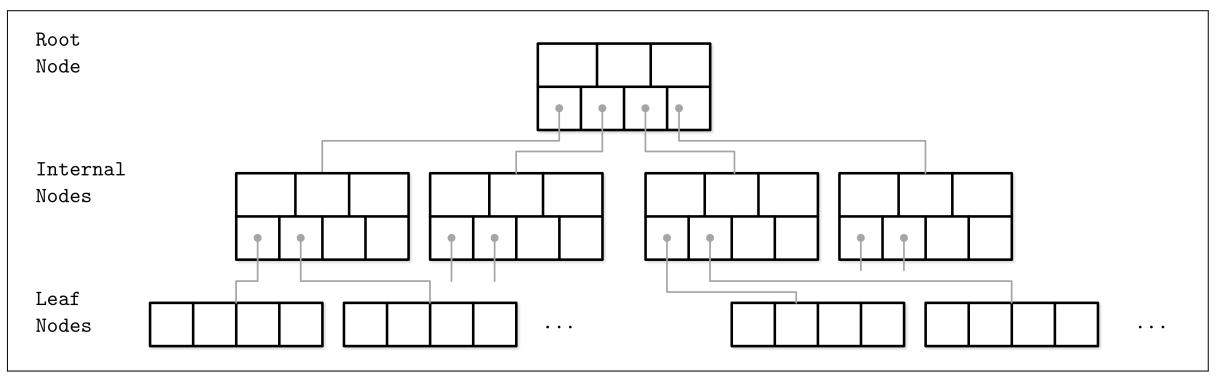
- Узел корня
Не имеет предков и является основной вершиной этого дерева.
- Узлы листьев
Это самые узлы самого нижнего уровня, которые не имеют дочерних узлов {терминальные узлы}.
- Внутренние узлы
Это все прочие узлы, соединяющие корень с листьями. Обычно имеется более одного уровня внутренних узлов {нетерминальные узлы}.
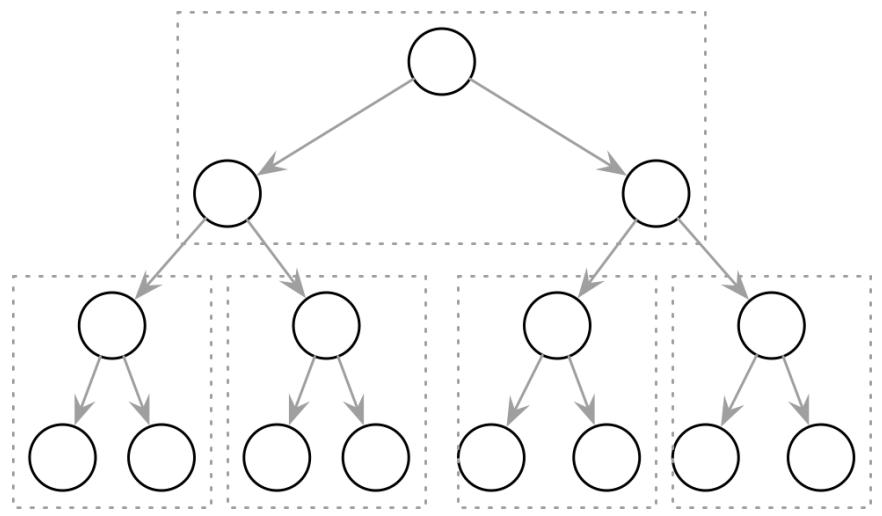
Эта иерархия показана на Рисунке 2-9.
Так как B- деревья являют технику организации страниц (то есть они используются для организации страниц с фиксированным размером и навигации по ним), мы часто будем взаимозаменяемо использовать термины узел и страница.
Значение соотношения между ёмкостью такого узла и общим числом ключей, которое он способен содержать именуется заполнением (occupancy).
B- деревья характеризуются их ветвлением (fanout): значением числа ключей, хранимых в каждом узле. Более высокая степень ветвления позволяет гасить общую стоимость структурных изменений, требуемых для удержания дерева в сбалансированном состоянии снижения числа позиционирований за счёт хранения ключей и указателей на дочерние узлы в неком отдельном блоке или во множестве последовательных блоков. Операции балансировки (а именно, расщепления и слияния) включаются когда эти узлы заполнены или почти пусты.
![[Замечание]](/common/images/admon/note.png) | B+- деревья |
|---|---|
|
Мы применяем термин B- дерева в качестве некого зонтика для структур данных, которые совместно применяют все или часть упомянутых свойств. Более точным названием для описываемой структуры данных является B+- деревья. [KNUTH98] ссылается на деревья с высоким порядком ветвления как на многоканальные (multiway) деревья. B- деревья позволяют хранить значения на любом уровне: в корневом, в промежуточных и листовых узлах. B+- деревья хранят значения только в узлах листьев. Внутренние узлы хранят лишь ключи разделения, применяемые как руководство для самого алгоритма поиска связанного значения, хранимого в соответствующем уровне листьев. Поскольку значения в B+- деревьях хранятся лишь на уровне листьев, все операции (вставка, обновление, удаление и выборка записей данных) воздействуют лишь на узлы листьев и распространяются на верхние уровни только в процессе расщеплений и слияний. B+- деревья приобрели широкое распространение и мы ссылаемся на них как на B- деревья, аналогично прочим литературным источникам по данной теме. Например, в [GRAEFE11] B+- деревья именуются как некое решение по умолчанию, а MySQL и InnoDB именуют свои реализации B+- деревьев B- деревом. |
Хранимые в B- деревьях ключи имеют название записей индекса, ключей разделителя или ячеек делителя. Они расщепляют само дерево на поддеревья (также именуемые ветвями или поддиапазонами), содержащими соответствующие диапазоны ключей. Ключи хранятся в неком сортированном порядке чтобы допускать двоичный поиск. Некое поддерево отыскивается по месту некого ключа и следованию соответствующему указателю с самого верхнего до самого нижнего уровней.
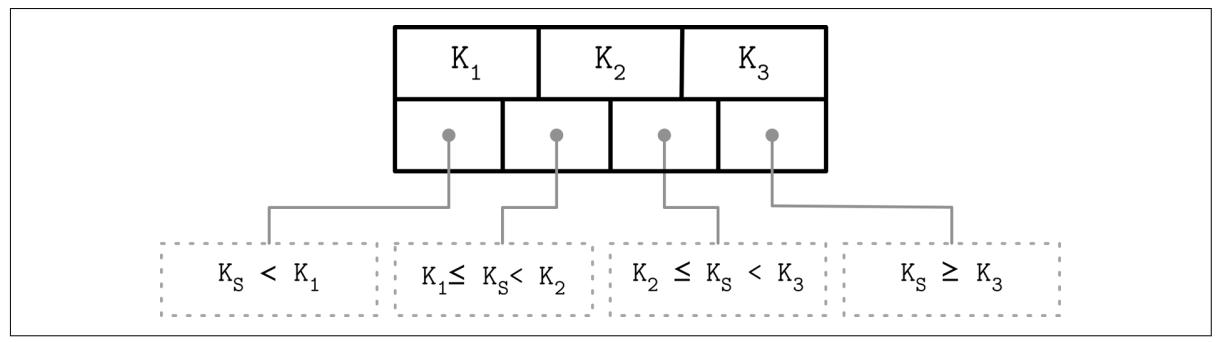
Самый первый указатель в таком узле указывает на то поддерево, которое содержит элементы
меньше чем значение первого ключа, а самый последний указатель в этом узле
указывает на то поддерево, которое содержит элементы больше чем или равные
значению для самого последнего ключа. Прочие указатели ссылаются на поддеревья между
значениями двух ключей: Ki-1 ≤ Ks < Ki, где
K это множество ключей, а Ks
это относящийся к определённому поддереву ключ. Рисунок 2-10 отображает такие инварианты.
Некоторые варианты поддеревьев также имеет братские указатели узлов, причём чаще всего на их уровне листьев для упрощения сканирования по диапазону. Такие указатели способствуют обходу возврата к своему родителю для обнаружения своего следующего брата. Некоторые реализации имеют указатели в обоих направлениях, формируя некий двунаправленный список связей на своём уровне листьев, что делает возможным обратные итерации.
Что отличает B- деревья, так это то, что они не создаются сверху вниз (в виде бинарных деревьев поиска), а наоборот - снизу вверх. Общее число листовых узлов растёт, что увеличивает общее число внутренних узлов и высоту дерева.
Поскольку B- деревья резервируют дополнительное пространство внутри узлов для последующих вставок и обновлений, использование хранилища дерева может достигать 50%, но обычно наблюдаются более высокие значения. Более высокая загруженность не оказывает влияние на производительность B- деревьев.
Сложность поиска в B- дереве может быть представлен с двух точек зрения: общего числа блочного обмена и общего числа сравнений, осуществляемых в процессе такого поиска.
В терминах числа обменов, значением основания логарифма выступает N
(числа ключей в узле). На каждом новом уровне имеется в K раз больше узлов, а
следуя за неким дочерним указателем снижает пространство поиска на значение множителя N.
В процессе поиска по крайней мере logK M (где
M это общее число элементов в этом B- дереве) страниц для решения поиска искомого
ключа. Общее число дочерних указателей, которым придётся следовать при проходе от вершины к листьям также равно общему
числу уровней, иными словами, значению высоты h данного дерева.
С точки зрения числа сравнений, значением основания логарифма является 2,
так как поиск ключа внутри каждого узла осуществляется при помощи двоичного поиска. Каждое сравнение делит пополам
пространство поиска, поэтому сложность равна log2 M.
Знание такого отличия между общим числом позиционирований и общим числом сравнений помогает нам получить интуитивное понимание относительно того как выполняются поиски и осознание какова сложность поиска, причём с обеих точек зрения.
В учебных руководствах и статьях (например, [KNUTH98]),
сложность поиска в B- дереве обычно приводится как log M. В анализе сложности
обычно не используется основание логарифма, так как изменение значения основания просто добавляет некий
постоянный множитель, а умножение на некий
постоянный множитель не изменяет сложность. Например, имея ненулевое значение постоянного множителя
c, O(|c| × n) == O(n)
[KNUTH97].
Теперь, когда мы рассмотрели саму структуру и внутреннюю организацию B- деревьев, мы можем определить алгоритмы для поиска, вставки и удалений. Для поиска некой записи в B- дереве нам приходится выполнять отдельный просмотр от корня до листа. Предметом такого поиска является обнаружение искомого ключа или его предка. Обнаружение точного соответствия применяется для запросов указания, обновлений и удалений; поиск его предка полезен для сканирований и вставок диапазона.
Такой алгоритм запускается с самого корня и осуществляет двоичный поиск, сравнивая значение искомого ключа с теми ключами, которые в узле самого корня пока не отыщет самый первый ключ разделителя, который больше чем величина искомого значения. Это определяет место искомого поддерева. Как мы уже обсуждали ранее, ключи индекса расщепляют своё дерево на поддеревья с границами между двумя соседними ключами. Как только мы находим искомое поддерево, мы следуем за тем указателем, который соответствует ему и продолжает тот же самый процесс поиска (определяет место значения ключа разделителя, следуя за его указателем) пока мы не достигнем некого целевого терминального узла, в котором мы либо обнаруживаем искомый ключ или делаем заключение что он не представлен в своём предке.
На каждом уровне мы получаем подробный просмотр своего дерева: мы начинаем с уровня с наибольшей грануляцией (корня данного дерева) и спускаемся на свой следующий уровень, на котором ключи представляют более точные, более подробные диапазоны до тех пор, пока мы не достигнем уровней, в которых расположены необходимые записи данных.
В процессе своего запроса указания данный поиск выполнен после обнаружения или неудачного результата для значения искомого ключа. На протяжении соответствующего сканирования диапазона итерации начинают с самого ближней найденной пары ключ- значение и продолжается по последующим братским указателям {того же самого уровня родства} пока не будет достигнут конец этого диапазона или не используется весь диапазон предиката.
В относящейся к данной теме литературе вы можете обнаружить различные способы описания счётчиков ключа и дочерних
смещений. [BAYER72] ссылается на определённое зависящее
от устройства натуральное число k, которое представляет некий оптимальный размер
страницы. В этом случае страницы способны содержать от k до
2k ключей, однако может быть частично заполненной от по крайней мере
k + 1 и максимально 2k + 1 указателями
на дочерние узлы. Узел корня может содержать от 1 до
2k ключей. Далее вводится некое число l и
утверждается, что любая нетерминальная страница может иметь l + 1 ключей.
Другие источники, к примеру, [GRAEFE11], описывают узлы
как способные содержать до N ключей разделителей
и N + 1 указателей, в остальном семантика
и инварианты аналогичны.
Оба подхода приводят нас к одному и тому же результату, и разнятся лишь применением выделением самого содержимого
каждого источника. В данной книге мы для ясности будем следовать N в качестве
общего числа ключей (или пар ключ- значение в случае терминальных узлов).
Для вставки соответствующего значения в некое B- джерево нам вначале требуется определить место своего целевого листа и найти точку вставки. Для этого мы используем описанный в нашем предыдущем разделе алгоритм. После локализации искомого листа, в его конец добавляются необходимые ключ и значение. Обновления в B- деревьях работают за счёт определения места некого целевого листа при помощи алгоритма просмотра и ассоциации с неким имеющимся ключом какого- то нового значения.
Когда наш целевой узел не обладает достаточным доступным пространством, мы говорим что этот узел переполнен [NICHOLS66] и приходится расщеплять его на два для помещения таких новых данных. Более точно, этот узел расщепляется при соблюдении следующих условий:
-
Для терминальных узлов: когда этот узел способен содержать до
Nпар ключ- значение и вставка ещё одной пары ключ- значение приводит к его к превышению максимальной ёмкостиN. -
Для не являющихся листьями {нетерминальных} узлов: если этот узел способен содержать до
N + 1указателей и вставка ещё одного указателя приводит его к превышению его максимальной ёмкостиN + 1.
Расщепление осуществляется посредством выделения необходимого нового узла, переноса в него половины его элементов из подвергающегося расщеплению узла и добавления его самого первого ключа и указателя в его родительский узел. В таком случае мы говорим что продвигается (promoted) новый ключ. Значение индекса, в котором выполняется данное расщепление имеет название точкой расщепления (также именующейся его средней точкой). Все элементы после такой точки расщепления (включая точку расщепления в случае деления нетерминального узла) перемещаются в такой вновь создаваемый братский {того же самого родственного уровня} узел, а все остальные элементы остаются в самом делимом узле.
Когда наш родительский узел заполнен и не обладает доступным пространством для таких продвигаемых ключа и указателя для своего вновь создаваемого узла, он также должен быть расщеплён. Эта операция может рекурсивно распространяться по всему пути до его корня.
После того как наше дерево достигает своей ёмкости (то есть расщепление преодолело весь путь вверх до своего корня), нам приходится расщеплять сам узел корня. После расщепления своего узла корня, выделяется некий новый корень, содержащий ключ точки расщепления. Наш старый корень (теперь содержащий лишь половину своих записей) переводится на свой следующий уровень совместно с его вновь созданным собратом, увеличивая значение высоты дерева на единицу. Значение высоты дерева изменяется при расщеплении его узла корня и выделении нового корня или когда два узла сливаются для формирования некого нового узла. На уровнях терминальных и промежуточных узлов само дерево растёт лишь горизонтально.
Рисунок 2-11 отображает полностью заполненный терминальный узел в процессе вставки
своего нового элемента 11. В самой середине такого заполненного узла мы проводим
соответствующую линию, оставляя половину его элементов в самом узле и перемещая все остальные элементы во вновь
создаваемый. Значение точки расщепления помещается в их родительский узел для того чтобы служить ключом разделителя.
Рисунок 2-11
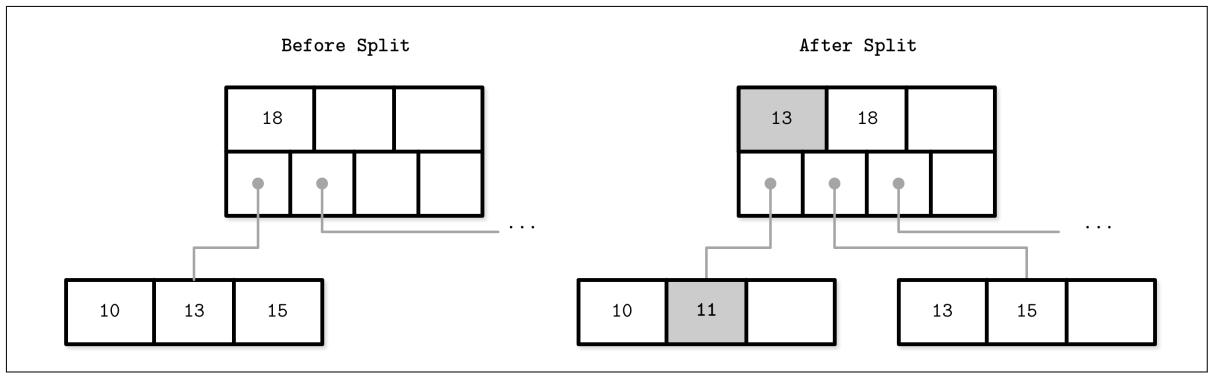
Расщепление терминального узла в процессе вставки
11.
Новый ключ и продвигаемый ключ показаны серым.
Рисунок 2-12 показывает соответствующий процесс расщепления полностью заполненного нетерминального
(то есть корневого или внутреннего) узла в процессе вставки нашего нового элемента 11.
Для выполнения расщепления мы вначале создаём какой- то новый узел и перемещаем в него элементы, начинающиеся с индекса
N/2 + 1. Сама точка расщепления продвигается в своего родителя.
Рисунок 2-12
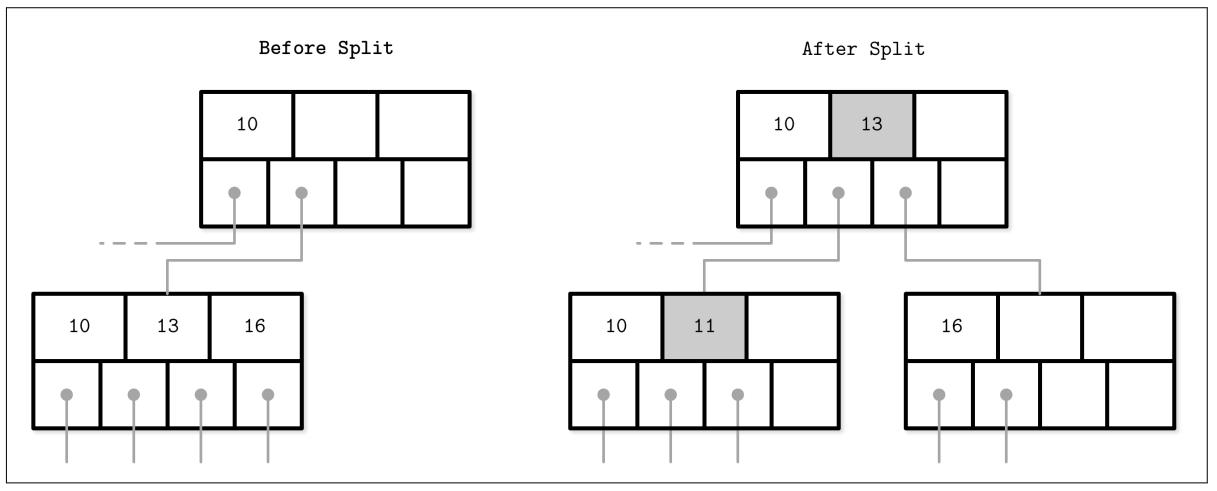
Расщепление нетерминального узла в процессе вставки
11.
Новый элемент и продвигаемый ключ показаны серым.
Поскольку расщепления нетерминального узла всегда некое олицетворение распространяемых с располагающихся ниже уровней расщеплений, мы получаем некий дополнительный указатель (на вновь создаваемый узел в своём следующем уровне). Когда его родитель не обладает достаточным пространством, его также приходится расщеплять.
Не имеет значения расщепляется ли терминальный или нетерминальный узел (то есть содержит ли этот узел ключи и значения или только сами ключи). В случае расщепления листа, ключи перемещаются совместно со связанными с ними значениями.
После завершения такого расщепления у нас имеются два узла и приходится прикрепляться к правильному для завершения вставки. Для этого мы можем применять инварианты значения ключа вставки. Если значение вставляемого ключа меньше чем значение продвигаемого, мы завершаем операцию вставкой в сам расщепляемый узел. В противном случае мы выполняем вставку во вновь созданный.
Чтобы подвести итог, расщепление узла выполняется четырьмя шагами:
-
Выделение нового узла.
-
Копирование половины элементов из расщепляемого узла во вновь созданный.
-
Помещение нового элемента в надлежащий узел.
-
Добавление ключа разделителя и указателя на вновб созданный узел в родителя расщепляемого узла.
Для удалений прежде всего нам необходимо определить место своего целевого листа. Когда этот лист найден, удаляются связанные с ним ключ и значение.
Если соседние узлы имеют слишком мало значений (то есть когда их занятость падает ниже порогового значения), такие находящиеся на одном родственном уровне узлы сливаются. Подобный случай имеет название потерей значимости (underflow, антипереполнением). [BAYER72] определяет два сценария потери значимости: если два смежных узла имеют общего предка и их содержимые помещаются в один узел, их содержимое следует слить (выполнить конкатенацию); когда их содержимое не умещается в одном узле, ключи перераспределяются между ними для восстановления баланса (см. Повторная балансировка). Более точно, два узла сливаются когда имеют место следующие обстоятельства:
-
Для терминальных узлов: когда этот узел способен содержать до
Nи сочетание числа пар ключ- значение в двух соседних узлах меньше чем или равноN. -
Для нетерминальных узлов: если этот узел способен содержать до
N + 1и сочетание числа пар ключ- значение в двух соседних узлах меньше чем или равноN + 1.
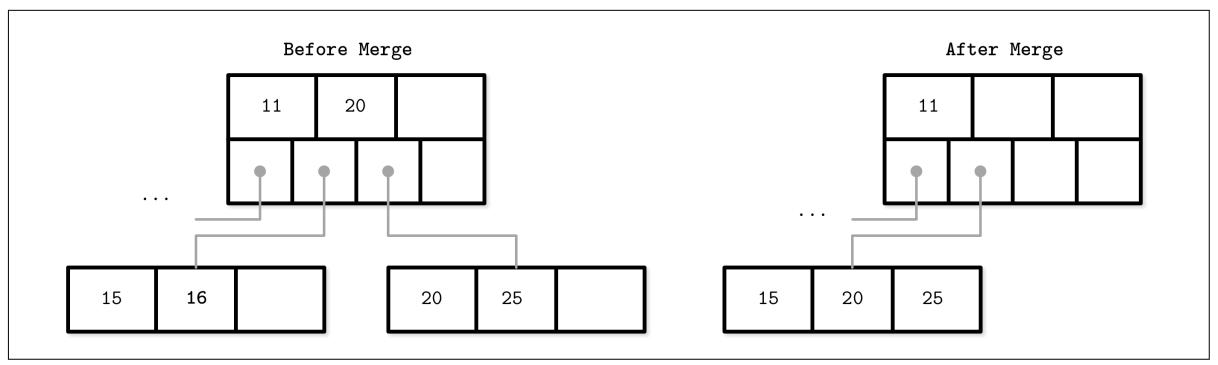
Рисунок 2-13 показывает слияние при удалении элемента 15. Для этого
мы перемещаем элементы из одного из братьев в другой. Как правило, элементы из первого
брата перемещаются в левого, но это может быть выполнено и иначе когда фиксирована
соответствующий порядок ключа.
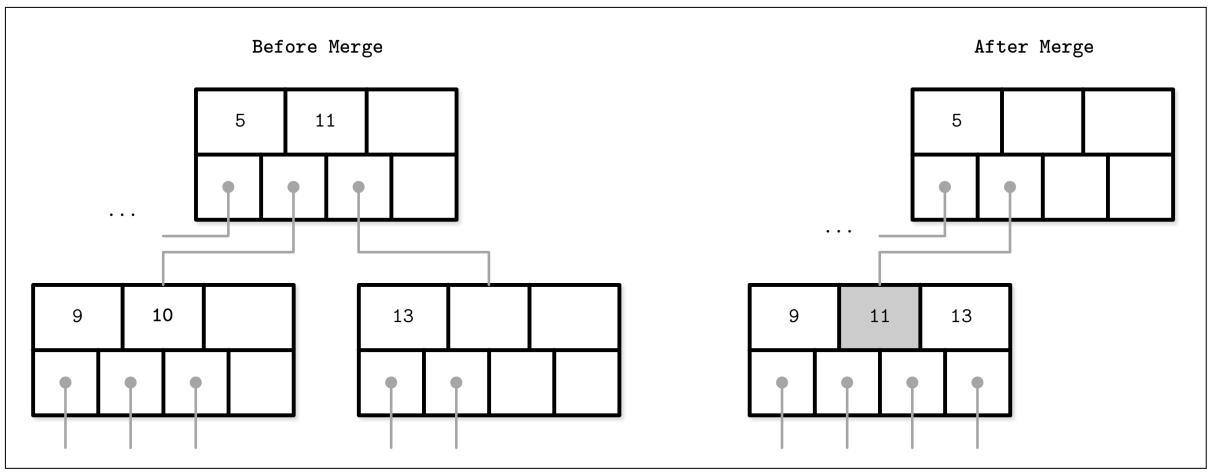
Рисунок 2-14 показывает два нетерминальных узла одного родственного уровня, которые подлежат слиянию в
процессе удаления элемента 10. Когда мы соединяем их элементы, они помещаются в
одном узле, поэтому мы можем иметь один узел вместо двух. В процессе слияния нетерминальных узлов, нам приходится вытолкнуть
соответствующий ключ разделителя из их родителей (то есть понизить его). Общее число указателей уменьшается на один,
так как подобное слияние является продвижением удаления соответствующего указателя с нижнего уровня, вызывающего удаления
надлежащей страницы. В точности как и при расщеплении, слияние способно продвигаться по всему пути до уровня корня.
Итак, чтобы суммировать, слияние узлов выполняется в три шага, в предположении что соответствующий элемент уже удалён:
-
Копируем все элементы из своего правого узла в левый.
-
Удаляем в их предке указатель на правый узел (либо понижаем его в случае слияния нетерминальных).
-
Удаляем свой правый узел.
Одной из технологий, часто реализуемой в B- деревьях для снижения общего числа расщеплений и слияний является ребалансировка, которая обсуждается в разделе Повторная балансировка.
В этой главе мы начали с мотивации для создания специальных структур для дискового хранения. Деревья двоичного поиска могут обладать аналогичными свойствами сложности, однко по- прежнему не подходят для дисков по причине низкой степени ветвления и большого числа перемещений и обновлений указателей, вызываемых балансировкой. B- деревья решают обе задачи увеличивая общее число хранимых в каждом узле элементов (более высокой степенью ветвления) и меньшей частотой операций балансировки.
После этого мы обсудили внутреннюю структуру B- деревьев и обозначили алгоритмы для операций поиска, вставки и удаления. Операции расщепления и слияния способствуют реструктуризации соответствиующего дерева для удержания его сбалансированным при добавлении и удалении элементов. Мы сохраняем высоту дерева минимальной и добавляем элементы в имеющиеся узлы пока в них существует свободное пространство.
Мы можем применять эти знания для создания B- деревьев в памяти. Для создания дисковой реализации нам потребуется углубиться в подробности того как выкладывать узлы B- дерева на диск и составить схему диска при помощи форматов кодирования данных.
![[Замечание]](/common/images/admon/note.png) | Последующее чтение |
|---|---|
|
Если вы желаете узнать больше относительно упоминавшихся в этой главе понятий, вы можете ссылаться на следующие источники:
|