Глава 4. Реализация B- деревьев
Содержание
В своей предыдущей главе мы обсуждали общие принципы составления двоичного формата и изучили как создавать ячейки, строить иерархии и подключать их к страницам при помощи указателей. Эти понятия приемлемы как для обновления по месту, так и для структур хранения исключительно с добавлением в конец. В этой главе мы обсудим некие понятия, являющиеся особенными для B- деревьев.
Разделы данной главы разбиты на три логические группы. Во- первых, мы обсуждаем организацию: как устанавливать взаимосвязь между ключами и указателями и как реализовывать заголовки и связи между страницами.
Затем мы обсуждаем процессы, которые происходят при спуске от корня- к- листьям, а именно как осуществлять двоичный поиск и как собирать хлебные крошки и отслеживать родительские узлы в случае, когда нам позднее приходится расщеплять или сливать узлы.
В конце концов, мы рассматриваем технологии оптимизации (повторную балансировку, доступные исключительно для чтения добавления в конец и пакетную загрузку), процессы сопровождения и сборку мусора.
Собственно заголовок страницы содержит сведения относительно самой страницы и может применяться для навигации, сопровождения и оптимизаций. Обычно он содержит флаги, которые описывают содержимое и схему страницы, число ячеек в этой странице, нижнее и верхнее смещения, отмечающие имеющееся свободное пространство (применяемое для добавления в конец смещений и данных ячеек), а также прочие полезные метаданные.
Например, PostgreSQL хранит в своём заголовке значение размера страницы и версию схемы. В MySQL InnoDB заголовок страницы содержит общее число записей заголовка, уровень и некие иные сведения, особые для реализации. В SQLite заголовок страницы хранит общее число ячеек и самый правый указатель.
Одним из значений, часто помещаемых в файл или заголовок страницы выступает магическое число. Обычно это некий блок из множества байт, содержащий некое постоянное значение, которое может применяться для сигнала о том, что этот блок представляет некую страницу, представляя её вид или идентифицируя её версию.
Магические числа часто используются для проверки подлинности и проверки корректности
[GIAMPAOLO98]. Очень важно чтобы эта последовательность байт по некому
произвольному смещению в строгости соответствовала данному магическому числу. Когда имеется соответствия, существует хорошая вероятность
того что это смещение верное. например, чтобы проверить что данная страница загружена и выровнена как положено, в процессе записи мы
можем помещать значение магического числа 50 41 47 45 (шестнадцатеричное значение для
PAGE). В процессе этого считывания мы можем подтвердить данную страницу, сопоставив эти четыре
байта из считанного заголовка с ожидаемой последовательностью байт.
Некоторые реализации хранят прямые и обратные ссылки, указывающие на самую левую и самую правую страницы одного уровня. Эти ссылки помогают определению места соседних узлов без необходимости подъёма вверх к своему родителю. Такой подход добавляет некую сложность в операции расщепления и слияния, поскольку также потребуется обновлять и такие братские смещения. Например, при расщеплении самого правого узла, его правый обратный указатель на собрата (ранее указывавший на тот узел который был расщеплён) должен быть подобран для указания на вновь созданный узел.
На Рисунке 4-1 вы можете наблюдать что для определения места братского узла, до тех пор, пока такие собратья не присоединены, нам придётся обращаться к своему родительскому узлу. Эта операция может подниматься по всему пути вплоть до корня, так как непосредственный родитель может выполнять адресацию лишь к своим собственным потомкам. Когда мы храним братские ссылки непосредственно в самом заголовке, мы можем просто следовать им для определения места своего предыдущего или последующего узла на том же самом уровне.
Рисунок 4-1
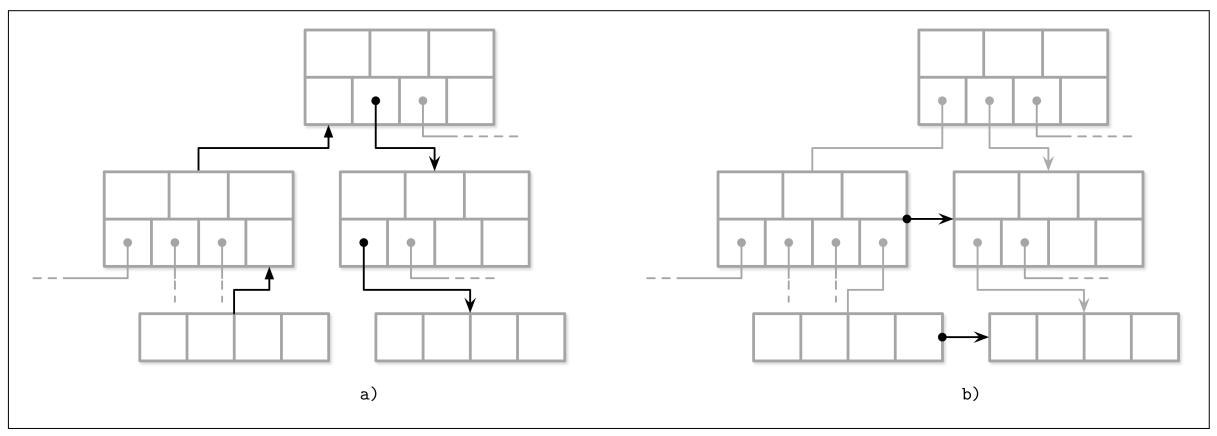
Сопоставление определения места собратьев путём следования родительским ссылкам (a) с прохождением по братским ссылкам (b)
Одним из недостатков хранения ссылок собратьев состоит в том, что они обязаны обновляться в процессе расщеплений и слияний. Так как обновления обязаны происходить в неком собратском узле, а не в узлах расщепления/ слияния, это может потребовать дополнительного блокирования. Мы обсудим то, насколько полезными могут быть ссылки собратьев в некой реализации одновременных B- деревьев в разделе Деревья Blink.
Ключи разделителя B- дерева имеют строгие инварианты: они применяются для расщепления данного дерева на поддеревья и навигации
по ним, поэтому всегда имеется на один указатель на дочерние страницы больше, чем имеется ключей. Это именно тот
+1, который упоминался ранее в разделе
Ключи счётчика.
В разделе Ключи разделители мы описывали инварианты ключи разделителя. Во многих реализациях узлы выглядят во многом похоже с тем как они отображены на Рисунке 4-2: каждый ключ разделителя обладает неким дочерним указателем, в то время как самый последний указатель хранится отдельно, так как у него нет в паре ни одного ключа. Вы можете сравнить это с Рисунком 2-10.
Такой дополнительный указатель может храниться в его заголовке, например, как это реализовано в SQLite.
Когда расщепляется крайний правый потомок и получаемый новый потомок добавляется в конец к своему предку, значение
самого правого указателя необходимо переназначить. Как показано на Рисунке 4-3, после такого расщепления полученная ячейка добавляется в конец своего предка (показана серым),
удерживая значение продвигаемого ключа и указывая на расщеплённый узел. Вместо значения предыдущего крайнего правого указателя
присваивается значение указателя на этот новый узел. Аналогичный подход описывается и реализуется в SQLite.
(Вы можете отыскать данный алгоритм в функции balance_deeper в
репозитории этого проекта.)
Рисунок 4-3
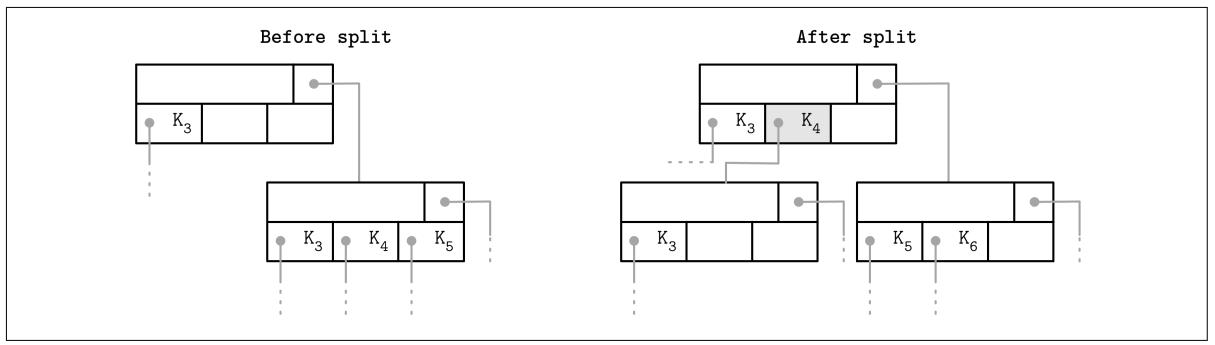
Обновление самого правого указателя в процессе расщепления узла. Продвигаемый ключ показан серым.
Мы можем предпринять несколько иной подход и сохранять и помимо крайнего правого указателя сохранять в соответствующей ячейке значения верхнего ключа (high key) узла. Это значение верхнего ключа представляет величину наивысшего возможного ключа, который может быть представлен в данном поддереве под текущим узлом. Такой подход применяется в PostgreSQL и имеет название Blink- деревьев (относительно реализаций данного подхода с одновременностью обратитесь к разделу Деревья Blink).
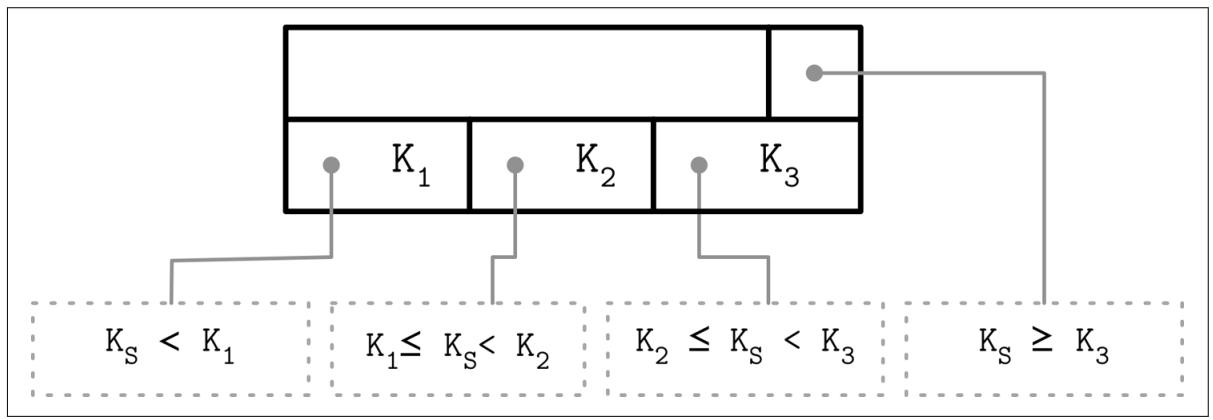
В- обладают N ключами (обозначаемыми как
Ki) и N + 1 указателями
(обозначаемыми как Pi). В каждом из поддеревьев ключи ограничены
Ki ≤ Ks < Ki. Подразумевается, что значение
K0 = -∞ и оно не представлено в этом узле.
Деревья Blink добавляют в каждый узел некий ключ
KN+1. Он определяет некую верхнюю границу ключей, которые могут храниться
в том поддереве, на который ссылается указатель PN
В данном случае указатели могут сохраняться попарно, причём каждая ячейка может обладать соответствующим указателем, который способен упрощать обработку крайнего правого указателя, ибо не приходится рассматривать множество граничных вариантов.
На Рисунке 4-5 вы можете наблюдать схематичную структуру страницы
для обоих подходов и то как отличается расщепление самого пространства поиска для таких вариантов проходя до +∞ в самом
первом случае и вверх до верхней границы K3 во втором.
Рисунок 4-5
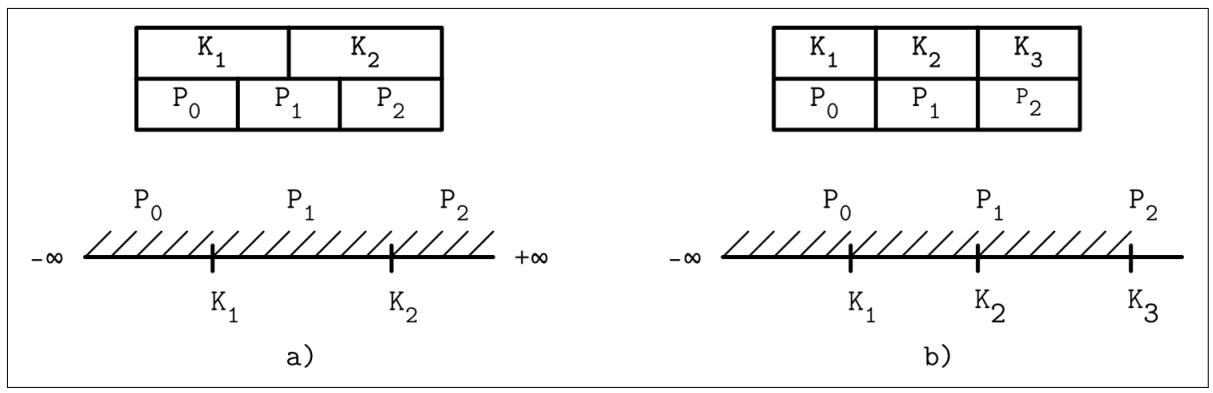
Применение +∞ как некого виртуального ключа (a) в сопоставлении со значением верхнего ключа (b)
Размер узла и развёртываемые значения дерева фиксированы и не изменятся динамически. Также было бы трудно прийти к такому значению, которое оказалось бы универсально оптимальным: когда в дереве имеются переменные значения размера, причём они достаточно велики, только некоторые из них могут помещаться на имеющейся странице. Когда же значения очень малы, мы в конце концов теряем зарезервированное пространство.
Установленный алгоритм B- дерева определяет что все узлы придерживаются предписанного числа элементов. Поскольку некие значения могут различаться в размерах, мы можем приходить в окончательном результате к тому случаю, при котором согласно определённому алгоритму B- дерева сам узел ещё пока не заполнен, но в нём больше нет свободного пространства при заданном фиксированном размере страницы, которые содержит этот узел. Изменение размера данной страницы потребует копирования уже записанных данных в некую новую область и часто оказывается не практичным. Тем не менее, нам всё ещё требуется поиск некого способа увеличения или расширения имеющегося размера страницы.
Для реализации узлов с переменным размером без копирования данных в новую непрерывную область мы можем выстраивать узлы из множества связанных страниц. Например, установленный по умолчанию размер страницы составляет 4k, а после вставки нескольких значений размер его данных превышает 4k. Вместо того чтобы допускать произвольные размеры, узлы позволяют рост приращениями по 4k, а потому мы выделяем некую страницу расширения в 4k и связываем её с первоначальной. Такие страницы расширения носят название страниц переполнения (overflow pages). В рамках данного раздела для ясности мы будем именовать свою оригинальную страницу первоначальной страницей (primary page).
Большинство реализаций B- дерева делают возможным хранение исключительно фиксированного числа байт полезной нагрузки в
своём узле B- дерева напрямую и вытеснять остальное в подобные страницы переполнения. Это значение вычисляется делением
установленного размера узла на расширение. Применяя такой подход, мы не сможем прийти к ситуации при которой данная страница не
имеет свободного пространства, поскольку она всегда будет иметь по крайней мере max_payload_size
байт. Для получения дополнительных сведений по страницам переполнения в SQLite, обратитесь к репозиторию исходного кода SQLite; а также проверьте
документацию MySQL InnoDB.
В случае когда размер вставляемой полезной нагрузки превышает max_payload_size,
такой узел проверяется на то имеет ли он уже какие бы то ни было связанные страницы переполнения. Когда такие страницы
переполнения уже имеются, и обладают достаточным доступным пространством, дополнительные байты из этой полезной нагрузки
вытесняются туда. В противном случае выделяется некая новая страница переполнения.
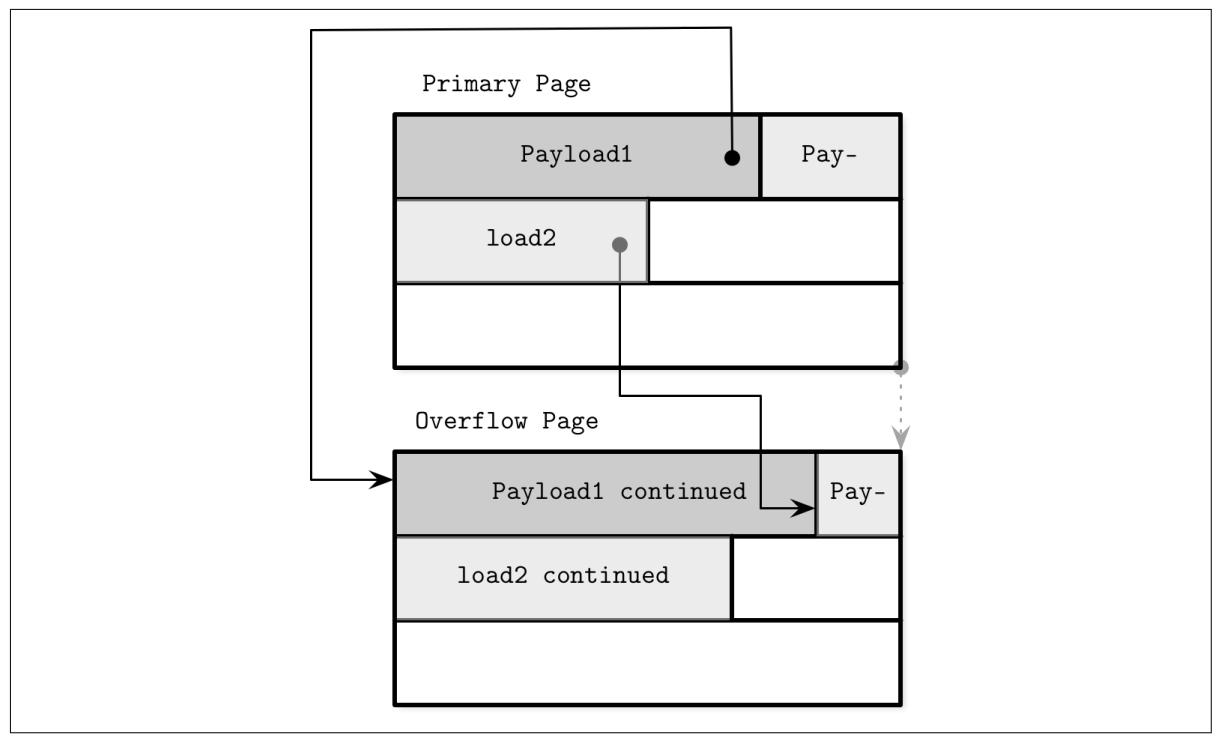
На Рисунке 4-6 мы можем видеть некую первичную страницу и страницу переполнения с записями, имеющими указатели со своей первоначальной страницы на страницу переполнения, в которой и продолжаются эта полезная нагрузка.
Страницы переполнения требуют некого дополнительного учёта, так как они могут быть фрагментированы так же как и первичные страницы и нам придётся иметь возможность возвращать это пространство для записи новых данных либо отбрасывать такие страницы переполнения когда они больше не требуются.
Когда выделяется самая первая страница переполнения, её идентификатор страницы сохраняется в имеющемся в такой первичной странице заголовке. Если некой отдельной страницы переполнения недостаточно, множество страниц переполнения связываются воедино путём сохранения идентификатора следующей необходимой страницы переполнения в заголовке своей предыдущей предшественницы. Для нахождения места необходимой части переполнения для заданной полезной нагрузки может потребоваться проход через несколько страниц.
Так как ключи обычно имеют высокую кардинальную мощность, имеет смысл хранить некую часть ключа, поскольку большая часть сравнений может выполняться для обрезанной части ключа, которая находится на самой первичной странице.
Для записей данных нам приходится определять их части переполнения для возврата таковых запрашивавшему пользователю. Тем не менее, это не существенно, поскольку это достаточно редкая операция. Когда все записи данных имеют большой размер данных, стоит рассмотреть возможность специализированного хранения blob для больших значений.
Мы уже обсуждали алгоритм поиска по B- дереву (см. Алгоритм поиска в В- деревьях) и упоминали, что мы определяем некий искомый ключ внутри данного узла с помощью алгоритма двоичного поиска. Двоичный поиск работает исключительно для сортированных данных. Когда ключи не упорядочены, по ним невозможно выполнять двоичный поиск. Именно по этой причине ключи отслеживают порядок и существенна поддержка неизменной сортировки.
Сам же алгоритм двоичного поиска получает некий массив сортированных элементов и некий искомый ключ, а возвращает некое число. Когда значение возвращаемого числа положительно, мы знаем что наш искомый ключ был найден, а значение числа определяет его положение в этом входном массиве. Некое отрицательное возвращаемое значение указывает что наш искомый ключ отсутствует в данном входном массиве и предоставляет нам точку вставки.
Эта точки вставки является значением индекса самого первого элемента, который больше чем заданное значение ключа. Абсолютное значение данного числа является значением индекса, по которому может быть вставлено значение искомого ключа с сохранением упорядоченности. Вставка может быть осуществлена сдвигом элементом на одну позицию, начиная с точки вставки для предоставления пространства данному вставляемому элементу [SEDGEWICK11].
Основная часть выполняемого поиска на более верхних уровнях не имеет результатом точного совпадения и мы выполняем вставку в направлении поиска и в этом случае нам приходится искать самое первое значение, которое больше чем искомое и следуем соответствующей дочерней связи в ассоциированном поддереве.
Ячейки в странице конкретного B- дерева хранятся в порядке вставки и лишь смещения ячеек удерживают имеющийся логический порядок элемента. Для выполнения двоичного поиска по ячейкам страницы мы берём значение смещения средней ячейки, следуем его указателю для определения места этой ячейки, сравниваем значение ключа из этой ячейки со значением искомого ключа для принятия решения по пути последующего поиска - вправо или налево, а затем рекурсивно продолжаем этот процесс пока не будет найден искомый элемент или необходимое место вставки, как это показано на Рисунке 4-7.
Рисунок 4-7
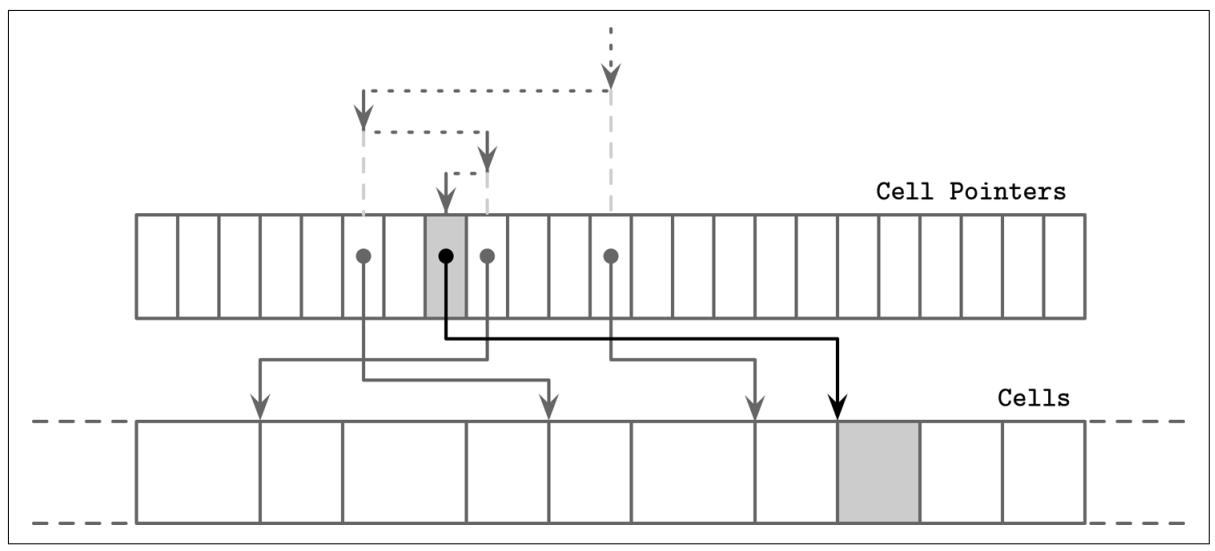
Двоичный поиск при помощи косвенных ссылок. Сам искомый элемент показан серым. Обозначенные пунктиром стрелки представляют двоичный поиск по указателям ячеек. Сплошные линии представляют доступы, которые следуют указателям этих ячеек, которые требуются для сравнения значений этих ячеек с неким искомым ключом.
Как мы уже обсуждали ранее в предыдущих главах, расщепления и слияния B- деревьев могут распространяться на более верхние уровни. Для этого нам требуется иметь возможность выполнять обход по некой цепочке обратно к узлу корня от расщепляемого листа или от сливаемых листьев.
Узлы B- деревьев могут содержать указатели на родительский узел. Поскольку страницы с нижних уровней всегда перемещаются по страницам когда на них ссылаются с более высокого уровня, нет необходимости в хранении этих сведений на диске.
Так же как и с указателями на собратьев (см. раздел Братские ссылки), указатели на родителей необходимо обновлять всякий раз когда изменяется такой предок. Это происходит во всех тех случаях, когда соответствующий ключ разделителя со значением идентификатора страницы передаётся от одного узла другому: в процессе расщепления узла его родителя, слияний или повторной балансировки имеющегося узла предка.
Некоторые реализации (к примеру, WiredTiger) применяют указатели родителей для обхода листьев во избежание взаимных блокировок, которые могут происходить при применении указателей собратьев (см. [MILLER78], [LEHMAN81]). Вместо применения братских указателей для обхода терминальных узлов такие алгоритмы держат в своём штате указатели на родителей, во многом подобно тому, что мы видели на Рисунке 4-1.
Для поиска и локализации собрата мы можем отслеживать указатель своего узла родителя и рекурсивно спускаться обратно на свой нижний уровень. Всякий раз когда мы достигаем самого конца своего родительского узла после обхода всех имеющихся собратьев, наш поиск продолжается рекурсивно вверх, в конечном итоге доходя до корня и возвращаясь обратно до уровня листьев.
Вместо того чтобы хранить и поддерживать указатели родительского узла имеется возможность отслеживать обход узлов по всему пути к целевому листовому узлу и следовать этой цепочке родительских узлов в обратном порядке в случае каскадных расщеплений в процессе вставок или слияний при удалении.
В прцессе действий, которые могут иметь результатом структурные изменения рассматриваемого B- дерева (вставок или удалений), мы вначале обходим всё дерево от его корня до искомого листа при обнаружении целевого узла и значения точки вставки. Так как мы не всегда знаем наперёд приведёт ли данная операция в результате к расщеплению или слиянию (по крайней мере до тех пор пока не будет обнаружен целевой листовой узел), нам приходится собирать хлебные крошки (breadcrumbs).
Хлебные крошки содержат ссылки на те узлы, которым мы следуем от своего корня и применяются для отслеживания пути назад по ним в обратном направлении при распространении расщеплений и слияний. Наиболее естественной структурой для этого выступает некий стек. Например, PostgerSQL хранит хлебные крошки в неком стеке, имеющим внутреннее название BTStack. (Дополнительно о нём можно прочесть в репозитории данного проекта).
При расщеплении или слиянии данного узла хлебные крошки могут применяться для поиска точек вставки для тех ключей, которые отправляют к родителям и для обратного прохода по рассматриваемому дереву при распространении структурных изменений к самым верхним узлам в случае такой необходимости. Этот стек поддерживается в оперативной памяти.
Рисунке 4-8 отображает некий образец обхода от корня к листу, сопровождаемому сбором хлебных крошек, содержащих указатели на посещённые узлы и индексы ячеек. Когда расщепляется определённый лист цели, его элемент на вершине имеющегося стека выталкивается из стека для определения метоположения его непосредственного предка. Когда такой родительский узел не обладает достаточным пространством, к нему в конец добавляется некая ячейка в его индексе ячеек из имеющихся хлебных крошек (в предположении что значение этого индекса всё ещё допустимо). В противном случае также расщепляется и сам родительский узел. Этот процесс рекурсивно продолжается пока либо не высвободится весь стек и мы не достигнем своего корня, либо нет расщеплений на текущем уровне.
Рисунок 4-8
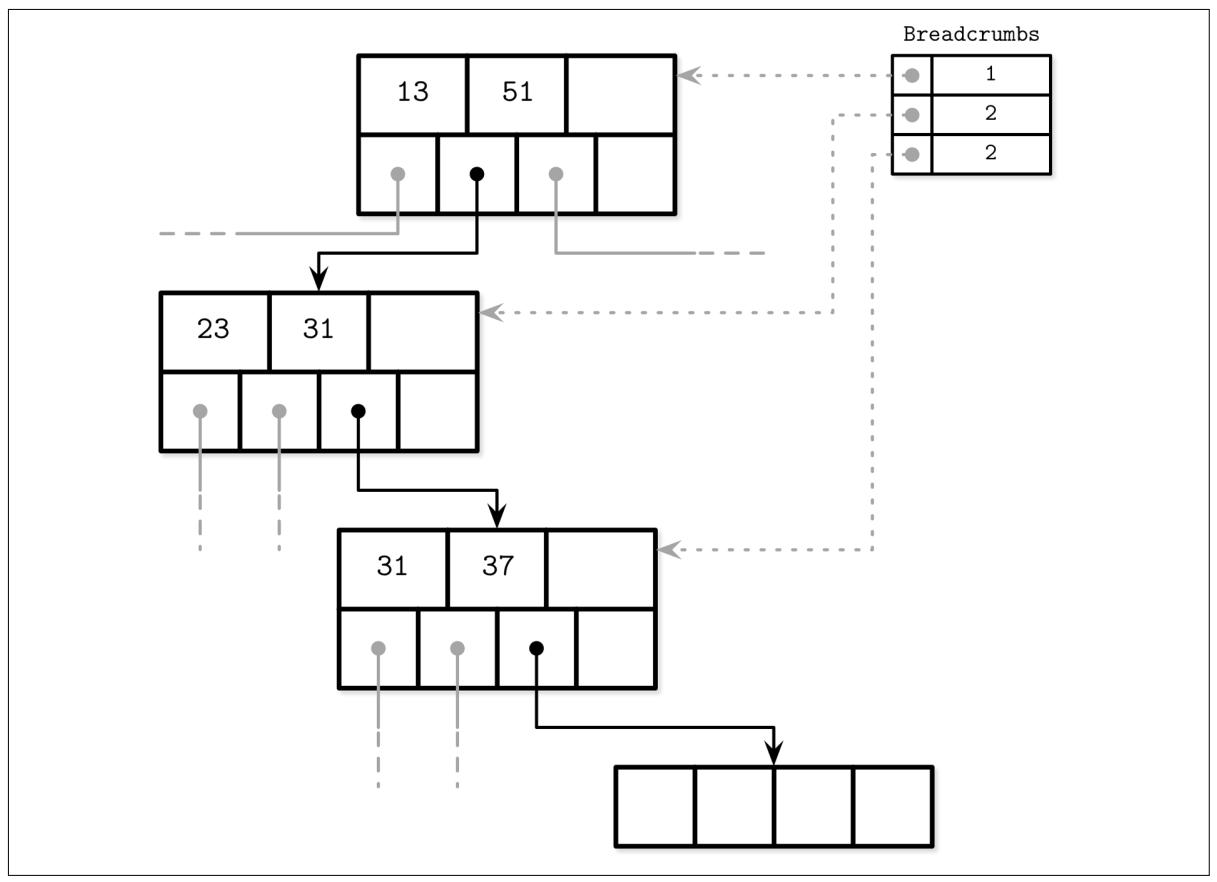
В процессе поиска собираются хлебные крошки, содержащие узлы обхода и индексы ячеек. Пунктирные линии представляют собой логические связи к посещённым узлам. Числа в самой таблице хлебных крошек представляют индексы пройденных дочерних указателей.
Некоторые реализации B- деревьев пытаются откладывать действия по расщеплению и слиянию чтобы отсрочить стоимости повторной балансировки элементов на определённом уровне или перемещения элементов из более занятых узлов в более свободные настолько долго, как только это возможно, прежде чем в конце концов выполнять расщепление или слияние. Это способствует улучшению занятости узлов и может снижать общее число уровней внутри рассматриваемого дерева с потенциалом более высокой стоимости повторной балансировки.
В процессе операций вставки и удалений может выполняться балансировка нагрузки [GRAEFE11]. С целью улучшения занятости пространства, вместо расщепления определённого узла переполнением, мы можем передавать некие элементы на один из узлов собратьев и создавать пространство для необходимой вставки. Аналогично, в процессе удаления, вместо того чтобы сливать братские узлы, мы можем выбрать перемещение определённых элементов с близлежащих узлов чтобы гарантировать что такой узел заполнен хотя бы наполовину.
B*- деревья распространяют данные по близлежащим узлам пока не заполнятся оба собрата [KNUTH98]. Затем, вместо расщепления отдельного узла на два заполненных наполовину, этот алгоритм расщепляет два узла на три узла, причём каждый заполнен на две трети. SQLite применяет именно этот вариант в своей реализации. такой подход улучшает значение средней занятости за счёт откладывания расщеплений, но требует дополнительной логики отслеживания и балансировки. Более высокая заполняемость также означает более действенные поиски, так как значение высоты получаемого дерева меньше и приходится обходить меньшее число страниц по пути к искомому листу.
Рисунок 4-9 показывает распределение элементов между двумя соседними узлами, при котором левый собрат содержит больше элементов чем правый. Элементы из более занятого узла перемещаются в более свободный. Так как балансировка изменяет значения минимума/ максимума инварианта в таких братских узлах, нам приходится обновлять ключи и указатели в соответствующем родительском узле для их сохранения.
Рисунок 4-9
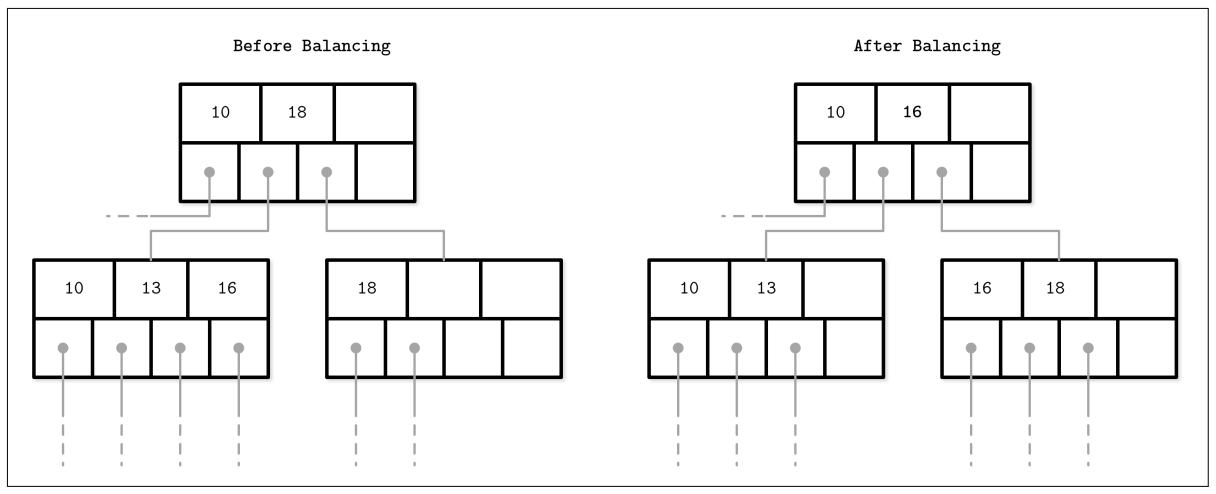
Балансировка B- дерева: Распространение элементов между более заполненными и менее занятыми узлами.
Балансировка нагрузки является полезной технологией, которая применяется в реализациях многих баз данных. Например, SQLite реализует алгоритм балансировки собратьев, который до определённой степени близок к тому, что мы описали в данном разделе. Балансировка может добавлять некую сложность в имеющемся коде, но так как её варианты применения изолированы, она может реализовываться в виде некой оптимизации на более поздней стадии.
Многие системы баз данных применяют в качестве первичных ключей индексов применяют монотонно увеличивающиеся значения с автоматическим приращением. Такой вариант открывает некую возможность для некой оптимизации, так все такие вставки происходят в самом конце значения индекса (в самом правом листе), поэтому наибольшая часть расщеплений происходит в самом правом узле на каждом уровне. Более того, поскольку значения ключей монотонно инкрементально увеличиваются, принимая во внимание что величина соотношения добавляемых в конец к обновляемым и удаляемым низка, не листовые страницы также менее фрагментированы нежели в случае упорядоченных случайным образом ключей.
PostgreSQL именует такой вариант как fastpath. Когда такой вставляемый ключ строго больше чем значение первого ключа в самой правой странице, а крайняя правая страница имеет достаточно места для хранения такой вновь вставляемой записи, эта новая запись вставляется в соответствующее место в своём кэшированном крайнем правом листе и можно пропустить считывание всего пути.
SQLite обладает аналогичным понятием и именует его quickbalance. Когда такая запись вставляется в самый правый конец и его целевой узел заполнен (т.е. она превращается в самую большую запись в рассматриваемом дереве после вставки), вместо того чтобы выполнять повторную балансировку или расщепление данного узла, выделяется место под необходимый новый крайний правый узел и добавляется ссылка на него в соответствующего родителя (относительно дополнительных сведений по реализации повторной балансировки в SQLite обратитесь к разделу Повторная балансировка. Даже несмотря на то, что это оставит такую вновь созданную страницу почти пустой (вместо наполовину пустой в случае расщепления узла), скорее всего этот узел вскорости заполнится.
Когда у нас имеются предварительно сортированные данные, а мы желаем загрузить их скопом или нам приходится перестраивать своё дерево (например, для дефрагментации), мы тем более можем воспользоваться той же мыслью, что и при добавлении в конец исключительно справа. Поскольку все необходимые для создания дерева данные уже отсортированы, в процессе пакетной загрузки (загрузки в навал) нам всего лишь требуется добавлять в конец соответствующие элементы в крайнее правое положение своего дерева.
В таком случае мы сможем вовсе избегать расщеплений и слияний и составлять своё дерево с самого низу, записывая его уровень за уровнем, либо записывая узлы верхнего уровня как только у нас будет достаточно указателей уже записанными в узлах нижнего уровня.
Один из подходов для реализации пакетной загрузки состоит в записи предварительно отсортированных данных на имеющемся листовом уровне по всем страницам (вместо вставки индивидуальных элементов). По окончанию записи листовой страницы мы продвигаем её самый первый ключ в её предка и применяем обычный алгоритм для построения верхних уровней B- дерева [RAMAKRISHNAN03]. Так как добавляемые в конец ключи заданы в сортированном порядке, все расщепления в этом случае происходят в крайнем правом узле.
Так как B- деревья всегда строятся с самого нижнего (листового) уровня, можно записать весь уровень листьев целиком прежде чем составлять какие бы то ни было узлы верхнего уровня. Это позволяет получить на руки все дочерние указатели в момент времени построения уровней высшего порядка. Основные преимущества такого подхода состоят в том, что нам не приходится выполнять какие бы то ни было расщепления и слияния на диске и в то же самое время отслеживать в памяти во время построения лишь минимальную часть всего дерева (то есть всех родителей заполняемых в настоящее время листовых узлов).
Неизменяемые B- деревья могут создаваться аналогичным образом, но, в отличии от изменяемых B- деревьев, они не требуют никакого дополнительного пространства для последующих изменений, так как все действия в дереве окончательные. Все страницы целиком заполнены, что улучшает заполненность и приводит в результате к лучшей производительности.
Хранение сырых, несжатых данных способно производить значительные накладные расходы и многие базы данных предлагают способы их сжатия для сохранения пространства. Очевидный компромисс здесь состоит между скоростью доступа и соотношением сжатия: большие значения соотношения сжатия могут улучшать размер данных, позволяя выборку большего объёма данных за один доступ, но может потребовать больше оперативной памяти и циклов ЦПУ для их сжатия и распаковки.
Сжатие может осуществляться на различных уровнях гранулярности. Даже хотя сжатие файлов целиком может выдавать наилучшие соотношения сжатия, оно ограничивает приложение, так как приходится распаковывать весь файл целиком при неком обновлении, а более гранулированное сжатие обычно лучше подходит для наборов данных большего размера. Сжатие всего индексного файла целиком как непрактично, так и тяжело реализовать действенным образом: для поиска определённой страницы приходится выполнять доступ (чтобы определить место в сжатом разделе) весь файл целиком (либо его раздел, содержащий сжатые метаданные), выполнить распаковку и сделать его доступным.
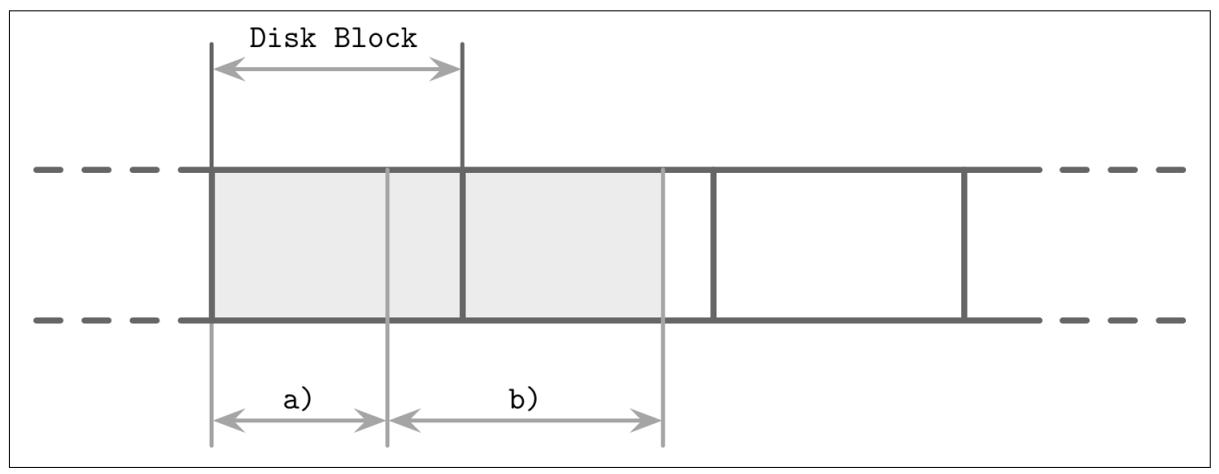
В качестве альтернативы выступает постраничное сжатие. Это хорошо подходит для нашего обсуждения, ибо те алгоритмы, которые мы до сих пор рассматривали, используют страницы с фиксированным размером. Страницы могут сжиматься и распаковываться независимо друг от друга, позволяя нам сочетать сжатие с загрузкой и сбросом страниц. Однако, некая сжатая страница в таком случае может занимать лишь часть некого дискового блока и, поскольку обмены обычно выполняются элементами дисковых блоков, может потребоваться размещать на странице дополнительные байты [RAY95]. На Рисунке 4-10 вы можете видеть некую сжатую страницу (a), занимающую пространство меньшее дискового блока. При загрузке этой страницы мы захватываем ею также некие дополнительные байты, которые относятся к другой странице. при страницах, которые охватывают множество дисковых блоков, как в случае на том же самом изображении, нам приходится считывать некий дополнительный блок.
Иной подход состоит в сжатии только данных либо по всей строке (сжатие данных записи целиком), либо по всему столбцу (индивидуальное сжатие столбца). В таком случае управление страницей и сжатие не связаны.
Большинство баз данных с открытым исходным кодом, рассмотренных при написании этой книги, обладали подключаемыми методами сжатия с применением доступных библиотек, таких как Snappy, zLib, lz4 и многие иные.
Поскольку алгоритмы сжатия дают различные результаты в зависимости от набора данных и потенциальных обстоятельств (т.е. соотношения сжатия, производительности или накладных расходов по памяти), мы не будем вдаваться в этой книге в подробности сравнения и реализации. Существует доступными множество обзоров, которые оценивают разнообразные алгоритмы сжатия для различных размеров блоков (например, Squash Compression Benchmark), обычно сосредоточенных на четырёх измерениях: накладных расходах памяти, производительности сжатия, производительности распаковки и соотношении сжатия. Эти измерения важны при рассмотрении выбора библиотеки сжатия.
До сих пор мы в основном обсуждали в B- деревьях операции стороны пользователя. Однако, существуют и иные процессы, которые происходят параллельно с запросами, которые поддерживают целостность, возврат пространства, снижение накладных расходов и удерживают упорядоченность страниц. Выполнение этих действий в фоновом режиме позволяет нам сберегать определённое время и избегать платы высокой стоимости за очистку в процессе вставок, обновлений и удалений.
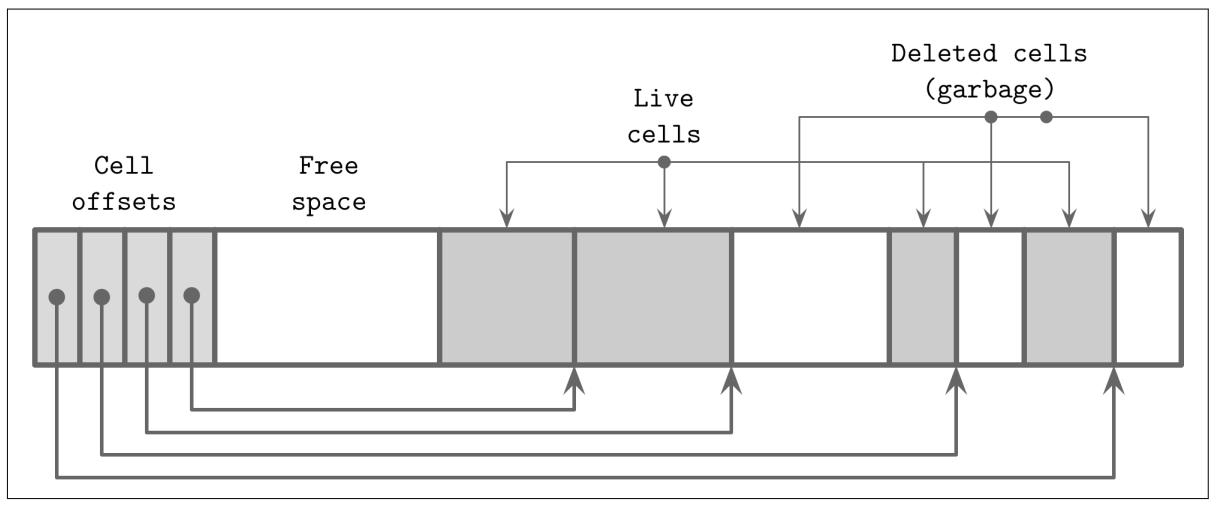
Описанная архитектура перекидных страниц (см. раздел Перекидные страницы) требует осуществления поддержки страниц для поддержки их в хорошей форме. Например, последовательные расщепления и слияния во внутренних узлах, либо вставки, обновления и удаления на уровне листьев могут иметь результатом то, что некая страница имеет достаточное логическое пространство, но не обладает достаточным непрерывным пространством по причине своей фрагментарности. Рисунок 4-11 отображает пример такого случая: эта страница всё ещё обладает доступным некое логическое пространство, однако оно фрагментировано и расщеплено между двумя удалёнными (мусорными) записями и неким остающимся свободным пространством между заголовком/ указателями ячеек и ячейками.
Навигация по B- деревьям выполняется с уровня его корня. Записи данных, которые можно достичь, следуя вниз по указателям из имеющегося коневого узла являются живыми (имеющими адреса), Записи данных без адресации именуются мусором: эти записи не имеют ссылок и не могут быть считаны или интерпретированы, а потому их содержимое настолько же полезно как заполненное нулями.
Вы можете наблюдать на Рисунке 4-11 эту разницу: те ячейки, которые всё ещё обладают сылающиеся на них указатели обладают адресами, в отличии от удалённых или перезаписанных. По соображениям производительности зачастую опускается заполнение нулями областей мусора, так как в конечном счёте эти области в любом случае перекрываются новыми данными.
давайте рассмотрим при каких обстоятельствах страницы приходят в состояние когда они имеют данные без адресации и подлежат уплотнению. На уровне листьев удаление лишь удаляет из имеющегося заголовка смещения ячеек, оставляя саму по себе ячейку нетронутой. После выполнения этого данная ячейка больше не адресуема, её содержимое более не появляется ни в каких результатах запросов, а её обнуление или удаление расположенных рядом ячеек не обязательно.
При расщеплении определённой страницы обрабатываются лишь смещения, так как весь остаток такой страницы не имеет адресов, те ячейки, смещения которых были отсечены более недостижимы, поэтому они буду перекрыты как только появятся новые данные или произойдёт сборка мусора при включении пылесоса.
![[Замечание]](/common/images/admon/note.png) | Замечание |
|---|---|
|
Некоторые базы данных полагаются на сборку мусора и оставляют удалённые и обновлённые ячейки на месте для контроля одновременности множества версий (см. раздел Управление одновременностью множества версий). Ячейки остаются доступными для одновременно исполняющихся транзакций пока не завершится данное обновление и могут быть собраны как только никакой иной поток не имеет к ним доступа. Некоторые базы данных поддерживают отслеживающие такие записи приведения (ghost) структуры, которые собираются как только завершены все транзакции, которые могли их просматривать [DECANDIA07]. |
Поскольку удаления лишь отбрасывают смещения ячеек и не перемещают остальные ячейки и физически также не удаляют целевые ячейки чтобы занять высвобожденное пространство, освобождение байт может в конце концов приводить к разбросу по всей странице. В таком случае мы говорим, что данная страница фрагментирована и требует дефрагментации.
Для выполнения записи нам часто требуется непрерывный блок свободных байт,в котором уместилась бы записываемая ячейка. Для того чтобы собрать обратно воедино все освобождённые фрагменты и исправить сложившуюся ситуацию нам приходится переписать данную страницу.
Операции вставки оставляют кортежи в их порядке вставки. Это не оказывает столь существенного воздействия, однако наличие естественной сортировки кортежей способно помогать при упреждающем кэшировании в процессе последовательных считываний.
Обновления по большей части применяются на уровне листьев: для руководства навигацией используются ключи внутренней страницы и лишь задают границы поддеревьев. Кроме того, обновления выполняются на основе ключей и в целом не имеют результатом структурных изменений в самом дереве, в отличии от создания страниц переполнения. На уровне листьев, тем не менее, операции обновления не изменяют порядок ячеек во избежание перезаписи страницы. Это означает, что из множества версий данной ячейки лишь одна, имеющая адресацию, может быть в конце конов сохранена.
Тот процесс, который заботится о возврате пространства и перезаписи страниц имеет название уплотнения (compaction), уборки (vacuum) или просто сопровождения. Перезаписи страниц могут выполняться синхронно с записью когда такая страница не обладает достаточным свободным физическим пространством (во избежание создания не нужных страниц переполнения), однако уплотнение чаще применяется для обозначения некого отличающегося, асинхронного, процесса обхода страниц с выполнением сборки мусора и переписываением их содержимого.
Такой процесс возвращает то пространство, которое занято убитыми ячейками и переписывает ячейки в их логическом порядке. При перезаписи страниц также может потребоваться новое положение в самом файле. Не используемые в памяти страницы становятся доступными и возвращаются в страничный кэш. Идентификаторы таких вновь доступных страниц на диске добавляются в список свободных страниц (порой именуемый свободным списком - freelist - например, SQLite поддерживает список страниц, которые ни применяются в его базе данных, в то время как соединительные - trunk - страницы удерживаются в неком связанном списке и содержат адреса высвобожденных страниц). Эти сведения обязаны быть постоянными для выживания при крушениях и повторных стартах и чтобы иметь уверенность что свободное пространство не потеряно и не утекает.
В этой главе мы обсудили основные понятия, являющиеся специфическими для реализаций B- деревьев на дисках, таких как:
- Заголовок страницы
Какие сведения обычно хранятся в нём.
- Крайние правые указатели
То, что они не являются парой для ключей разделителей, а также как их обрабатывать.
- Верхние ключи
Определяют максимальное значение ключей, которые допускается хранить в данном узле.
- Страницы переполнения
Позволяют вам хранить излишки и записи переменной длины с применением страниц фиксированного размера.
После этого мы прошлись по некоторым подробностям, относящимся к проходам от корня к листу:
-
Как осуществлять двоичный поиск при помощи косвенных указателей
-
Как отслеживать иерархии дерева пользуясь родительскими указателями или хлебными крошками
Наконец, мы прошлись по некоторым технологиям оптимизации и сопровождения:
- Повторная балансировка
Перемещает элементы между соседними узлами для снижения числа расщеплений и слияний.
- Исключительно крайние правые добавления в конец
Добавляют в конец новую самую правую ячейку вместо её расщепления в предположении что она скоро заполнится.
- Пакетная загрузка
Технология для эффективного построения B- деревьев с нуля из сортированных данных.
- Сборка мусора
Некий процесс, который перезаписывает страницы, помещая ячейки в порядке ключей и возвращая пространство, занимаемое ячейками без адресации.
Эти понятия должны навести мост между основным алгоритмом B- дерева и реализацией реального мира и помочь вам лучше понять как работают основанные на B- дереве системы хранения.
![[Замечание]](/common/images/admon/note.png) | Последующее чтение |
|---|---|
|
Если вы желаете узнать больше относительно упоминавшихся в этой главе понятий, вы можете ссылаться на следующие источники:
|